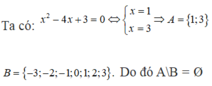Đáp án C

bài dễ ợt mà làm ko đc

Không làm mất tính tổng quát, giả sử \(0< x\le y\le z\)

=> \(x+y+z\le3z\Leftrightarrow xyz\le3z\Leftrightarrow xy\le3\)

Mà x;y;z là các số nguyên dương => \(xy\in\left\{1;2;3\right\}\)

Ta xét các trường hợp: 

TH1: \(xy=1\Leftrightarrow\hept{\begin{cases}x=1\\y=1\end{cases}}\Leftrightarrow2+z=z\Leftrightarrow2=0\) (vô lý!)

TH2: \(xy=2\Leftrightarrow\hept{\begin{cases}x=1\\y=2\end{cases}}\Leftrightarrow z=3\) (thỏa mãn)

TH3: \(xy=3\Leftrightarrow\hept{\begin{cases}x=1\\y=3\end{cases}}\Leftrightarrow z=2\) (thỏa mãn)

Vậy (x;y;z) là các hoán vị của (1;2;3)

\(A=\left|2x+2\right|+\left|2x-2013\right|=\left|2x+2\right|+\left|2013-2x\right|\)

Áp dụng bất đẳng thức \(\left|a\right|+\left|b\right|\ge\left|a+b\right|\)với \(ab\ge0\)

=>\(A=\left|2x+2\right|+\left|2013-2x\right|\ge\left|2x+2+2013-2x\right|=2015\) 

với \(\left(2x+2\right)\left(2013-2x\right)\ge0\)

=>\(A_{min}=2015\) với  \(-0,5\le x\le1006,5\)

a: \(\text{Δ}=\left[-\left(m+3\right)\right]^2-4\cdot2\cdot m\)

\(=\left(m+3\right)^2-8m\)

\(=m^2-2m+9=\left(m-1\right)^2+8>0\forall m\)

=>Phương trình (1) luôn có hai nghiệm phân biệt

b: Theo Vi-et, ta có:

\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=\dfrac{m+3}{2}\\x_1\cdot x_2=\dfrac{c}{a}=\dfrac{m}{2}\end{matrix}\right.\)

\(A=\left|x_1-x_2\right|=\sqrt{\left(x_1-x_2\right)^2}\)

\(=\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}\)

\(=\sqrt{\dfrac{1}{4}\left(m+3\right)^2-4\cdot\dfrac{m}{2}}\)

\(=\sqrt{\dfrac{1}{4}\left(m^2+6m+9\right)-2m}\)

\(=\sqrt{\dfrac{1}{4}m^2+\dfrac{3}{2}m+\dfrac{9}{4}-2m}\)

\(=\sqrt{\dfrac{1}{4}m^2-\dfrac{1}{2}m+\dfrac{9}{4}}\)

\(=\sqrt{\dfrac{1}{4}\left(m^2-2m+9\right)}\)

\(=\sqrt{\dfrac{1}{4}\left(m^2-2m+1+8\right)}\)

\(=\sqrt{\dfrac{1}{4}\left(m-1\right)^2+2}>=\sqrt{2}\)

Dấu '=' xảy ra khi m-1=0

=>m=1

Chọn đáp án A

x 2  + 2x - 5 = 0 phương trình có ac < 0 ⇒ phương trình có 2 nghiệm phân biệt

Theo định lí Vi-et ta có:

\(x^2-2\left(m-1\right)x+m-5=0\)

Xét \(\Delta=4\left(m-1\right)^2-4\left(m-5\right)=4m^2-12m+24\)\(=\left(2x-3\right)^2+15>0\forall m\)

=>Pt luôn có hai nghiệm pb

Theo viet:\(\left\{{}\begin{matrix}x_1+x_2=2\left(m-1\right)\\x_1x_2=m-5\end{matrix}\right.\)

Đặt \(A=\left|x_1-x_2\right|\)

\(\Rightarrow A^2=\left(x_1-x_2\right)^2=\left(x_1+x_2\right)^2-4x_1x_2\)

\(=4\left(m-1\right)^2-4\left(m-5\right)=4m^2-12m+24\)

\(=\left(2m-3\right)^2+15\ge15\)

\(\Rightarrow A\ge\sqrt{15}\)

\(A_{min}=\sqrt{15}\Leftrightarrow m=\dfrac{3}{2}\)