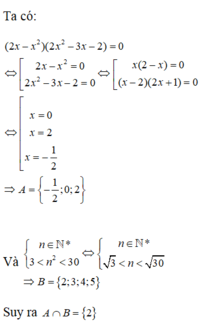Câu 2: 

\(\left(A\cup B\right)\cap C=A\cap C=[1;+\infty)\cap\left(0;4\right)=[1;4)\)

Tập này có 3 phần tử nguyên

Đáp án B

`#3107.101107`

a,

\(\text{A = }\left\{x\in R\text{ | }\left(2x-x^2\right)\left(3x-2\right)=0\right\}\)

`<=> (2x - x^2)(3x - 2) = 0`

`<=>`\(\left[{}\begin{matrix}2x-x^2=0\\3x-2=0\end{matrix}\right.\)

`<=>`\(\left[{}\begin{matrix}x\left(2-x\right)=0\\3x=2\end{matrix}\right.\)

`<=>`\(\left[{}\begin{matrix}x=0\\2-x=0\\x=\dfrac{2}{3}\end{matrix}\right.\)

`<=>`\(\left[{}\begin{matrix}x=0\\x=2\\x=\dfrac{2}{3}\end{matrix}\right.\)

Vậy, `A = {0; 2; 2/3}`

b,

\(\text{B = }\left\{x\in R\text{ | }2x^3-3x^2-5x=0\right\}\)

`<=> 2x^3 - 3x^2 - 5x = 0`

`<=> x(2x^2 - 3x - 5) = 0`

`<=>`\(\left[{}\begin{matrix}x=0\\2x^2-3x-5=0\end{matrix}\right.\)

`<=>`\(\left[{}\begin{matrix}x=0\\2x^2-2x+5x-5=0\end{matrix}\right.\)

`<=>`\(\left[{}\begin{matrix}x=0\\\left(2x^2-2x\right)+\left(5x-5\right)=0\end{matrix}\right.\)

`<=>`\(\left[{}\begin{matrix}x=0\\2x\left(x-1\right)+5\left(x-1\right)=0\end{matrix}\right.\)

`<=>`\(\left[{}\begin{matrix}x=0\\\left(2x+5\right)\left(x-1\right)=0\end{matrix}\right.\)

`<=>`\(\left[{}\begin{matrix}x=0\\2x+5=0\\x-1=0\end{matrix}\right.\)

`<=>`\(\left[{}\begin{matrix}x=0\\x=-\dfrac{5}{2}\\x=1\end{matrix}\right.\)

Vậy, `B = {-5/2; 0; 1}.`

c,

\(\text{C = }\left\{x\in Z\text{ | }2x^2-75x-77=0\right\}\)

`<=> 2x^2 - 75x - 77 = 0`

`<=> 2x^2 - 2x + 77x - 77 = 0`

`<=> (2x^2 - 2x) + (77x - 77) = 0`

`<=> 2x(x - 1) + 77(x - 1) = 0`

`<=> (2x + 77)(x - 1) = 0`

`<=>`\(\left[{}\begin{matrix}2x+77=0\\x-1=0\end{matrix}\right.\)

`<=>`\(\left[{}\begin{matrix}2x=-77\\x=1\end{matrix}\right.\)

`<=>`\(\left[{}\begin{matrix}x=-\dfrac{77}{2}\\x=1\end{matrix}\right.\)

Vậy, `C = {-77/2; 1}`

d,

\(\text{D = }\left\{x\in R\text{ | }\left(x^2-x-2\right)\left(x^2-9\right)=0\right\}\)

`<=> (x^2 - x - 2)(x^2 - 9) = 0`

`<=>`\(\left[{}\begin{matrix}x^2-x-2=0\\x^2-9=0\end{matrix}\right.\)

`<=>`\(\left[{}\begin{matrix}x^2+x-2x-2=0\\x^2=9\end{matrix}\right.\)

`<=>`\(\left[{}\begin{matrix}\left(x^2+x\right)-\left(2x+2\right)=0\\x^2=\left(\pm3\right)^2\end{matrix}\right.\)

`<=>`\(\left[{}\begin{matrix}x\left(x+1\right)-2\left(x+1\right)=0\\x=\pm3\end{matrix}\right.\)

`<=>`\(\left[{}\begin{matrix}\left(x-2\right)\left(x+1\right)=0\\x=\pm3\end{matrix}\right.\)

`<=>`\(\left[{}\begin{matrix}x-2=0\\x+1=0\\x=\pm3\end{matrix}\right.\)

`<=>`\(\left[{}\begin{matrix}x=2\\x=-1\\x=\pm3\end{matrix}\right.\)

Vậy, `D = {-1; -3; 2; 3}.`

a) Ta có: (2x² - 5x + 3)(x² - 4x + 3) = 0

=> \(\orbr{\begin{cases}2x^2-5x+3=0\\x^2-4x+3=0\end{cases}}\)

=> \(\orbr{\begin{cases}2x^2-2x-3x+3=0\\x^2-3x-x+3=0\end{cases}}\)

=> \(\orbr{\begin{cases}2x\left(x-1\right)-3\left(x-1\right)=0\\x\left(x-3\right)-\left(x-3\right)=0\end{cases}}\)

=> \(\orbr{\begin{cases}\left(2x-3\right)\left(x-1\right)=0\\\left(x-1\right)\left(x-3\right)=0\end{cases}}\)

=> x = 3/2 hoặc x = 1

hoặc : x = 1 hoặc x = 3

=> Tập hợp A = {1; 3/2; 3}

b) Ta có: (x² - 10x + 21)(x³ - x) = 0

=> (x² - 7x - 3x + 21)x(x² - 1) = 0

=> [x(x - 7) - 3(x - 7)x(x² - 1) = 0

=> (x - 3)(x - 7)x(x - 1)(x+ 1) = 0

=> x - 3 = 0 hoặc x - 7 = 0 hoặc x = 0 hoặc x - 1 = 0 hoặc x + 1 = 0

=> x = 3 hoặc x = 7 hoặc x = 0 hoặc x = 1 hoặc x = -1

=> Tập hợp B = {-1; 0; 1; 3; 7}

mày điên à đây là mini world à  đây không phải toán lớp 1 con ngu

a: \(A=\left\{1;-5\right\}\)

b: \(B=\left\{1;2\right\}\)

c: \(C=\left\{0;1;4;9;16;25;36;49\right\}\)

d: \(D=\left\{1;2;3;6\right\}\)

e: E={8}

\(A=\left\{x\in R|\left(x-2x^2\right)\left(x^2-3x+2\right)=0\right\}\)

Giải phương trình sau :

 \(\left(x-2x^2\right)\left(x^2-3x+2\right)=0\)

\(\Leftrightarrow x\left(1-2x\right)\left(x-1\right)\left(x-2\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\1-2x=0\\x-1=0\\x-2=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{1}{2}\\x=1\\x=2\end{matrix}\right.\)

\(\Rightarrow A=\left\{0;\dfrac{1}{2};1;2\right\}\)

\(B=\left\{n\in N|3< n\left(n+1\right)< 31\right\}\)

Giải bất phương trình sau :

\(3< n\left(n+1\right)< 31\)

\(\Leftrightarrow\left\{{}\begin{matrix}n\left(n+1\right)>3\\n\left(n+1\right)< 31\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}n^2+n-3>0\\n^2+n-31< 0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}n< \dfrac{-1-\sqrt[]{13}}{2}\cup n>\dfrac{-1+\sqrt[]{13}}{2}\\\dfrac{-1-5\sqrt[]{5}}{2}< n< \dfrac{-1+5\sqrt[]{5}}{2}\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{-1-5\sqrt[]{5}}{2}< n< \dfrac{-1-\sqrt[]{13}}{2}\\\dfrac{-1+\sqrt[]{13}}{2}< n< \dfrac{-1+5\sqrt[]{5}}{2}\end{matrix}\right.\)

Vậy \(B=\left(\dfrac{-1-5\sqrt[]{5}}{2};\dfrac{-1-\sqrt[]{13}}{2}\right)\cup\left(\dfrac{-1+\sqrt[]{13}}{2};\dfrac{-1+5\sqrt[]{5}}{2}\right)\)

\(\Rightarrow A\cap B=\left\{2\right\}\)

b: A là tập con của B

A là tập con của C

A là tập con của D và ngược lại