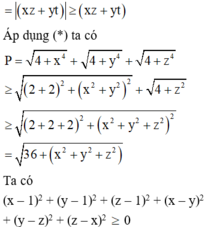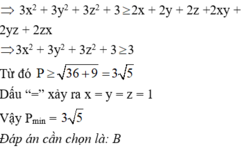Ta có \(2A=20x^2+20y^2+2z^2=\left(z^2+16x^2\right)+\left(z^2+16y^2\right)+4\left(x^2+y^2\right)\)

\(\ge2z\cdot4x+2z\cdot4y+4\cdot2xy=8\left(xy+yz+zx\right)=8\to A\ge4.\)

Dấu bằng xảy ra khi \(z=4x=4y,1=xy+yz+zx=x^2+4x^2+4x^2=9x^2\to x=y=\pm\frac{1}{3},z=\pm\frac{4}{3}.\)

Vậy giá trị bé nhất của \(A\) bằng \(4.\)

Xét nào:)

Từ giả thiết suy ra x + y + z > 3

Ta có: \(P=2x^2+xy+2y^2=\frac{5}{4}\left(x+y\right)^2+\frac{3}{4}\left(x-y\right)^2\ge\frac{5}{4}\left(x+y\right)^2\)

Suy ra \(\sqrt{2x^2+xy+y^2}\ge\sqrt{\frac{5}{4}}.\left(x+y\right)=\frac{\sqrt{5}}{2}\left(x+y\right)\)

Tương tự hai BĐT còn lại và cộng theo vế: \(P\ge\sqrt{5}\left(x+y+z\right)\ge3\sqrt{5}\)

Đẳng thức xảy ra khi x = y = z = 1

Is it right?!?

thank ban

bạn giải thích rõ hộ mình dòng 2 với

\(\sqrt{x^2+2024}=\sqrt{x^2+xy+yz+zx}=\sqrt{\left(x+y\right)\left(z+x\right)}\ge\sqrt{\left(\sqrt{xz}+\sqrt{xy}\right)^2}=\sqrt{xy}+\sqrt{xz}\)

Tương tự: \(\sqrt{y^2+2024}\ge\sqrt{xy}+\sqrt{yz}\)

\(\sqrt{z^2+2024}\ge\sqrt{xz}+\sqrt{yz}\)

Cộng vế:

\(P\ge\dfrac{2\left(\sqrt{xy}+\sqrt{yz}+\sqrt{zx}\right)}{\sqrt{xy}+\sqrt{yz}+\sqrt{zx}}=2\)

Dấu "=" xảy ra khi \(x=y=z=\dfrac{2024}{3}\)

Đề sai rồi còn làm gì:)))