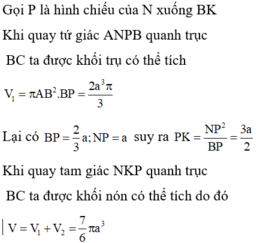Cho hình vuông ABCD. M,N thuộc BC,CD sao cho CM=2DN. P thuộc AD sao cho MP vuông góc AN, CMR DN=DP

Những câu hỏi liên quan
Cho hình thang vuông ABCD vuông tại A và D. Có hai đáy AB song song với CD. Gọi M là trung điểm của đoạn thẳng AD. Điểm P và Q thuộc BC sao cho BP= CQ . Cho biết rằng MQ vuông góc với DP. Chứng minh rằng MP vuông góc với AQ.
Hình vẽ minh họa, sử dụng tính chất trực tâm của tam giác.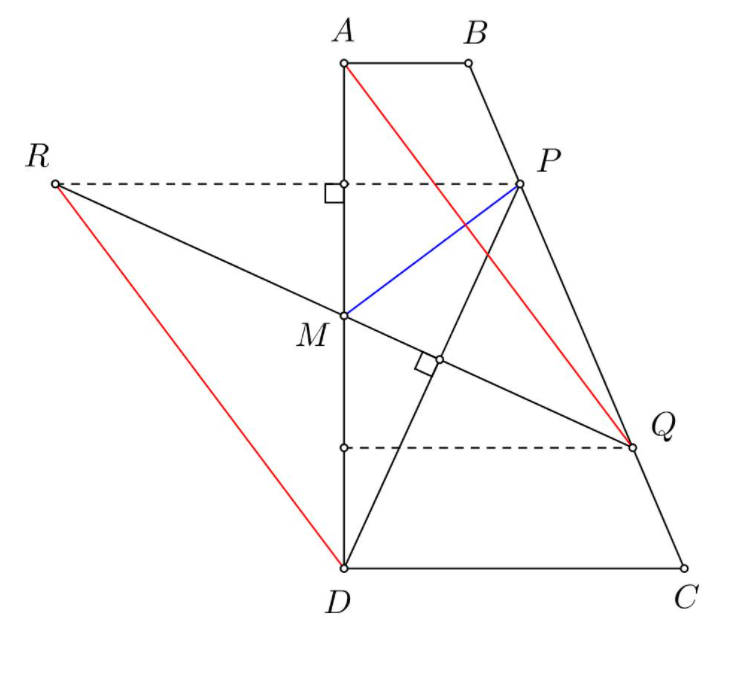
Đúng 0
Bình luận (1)
Sử dụng tính chất trực tâm của tam giác .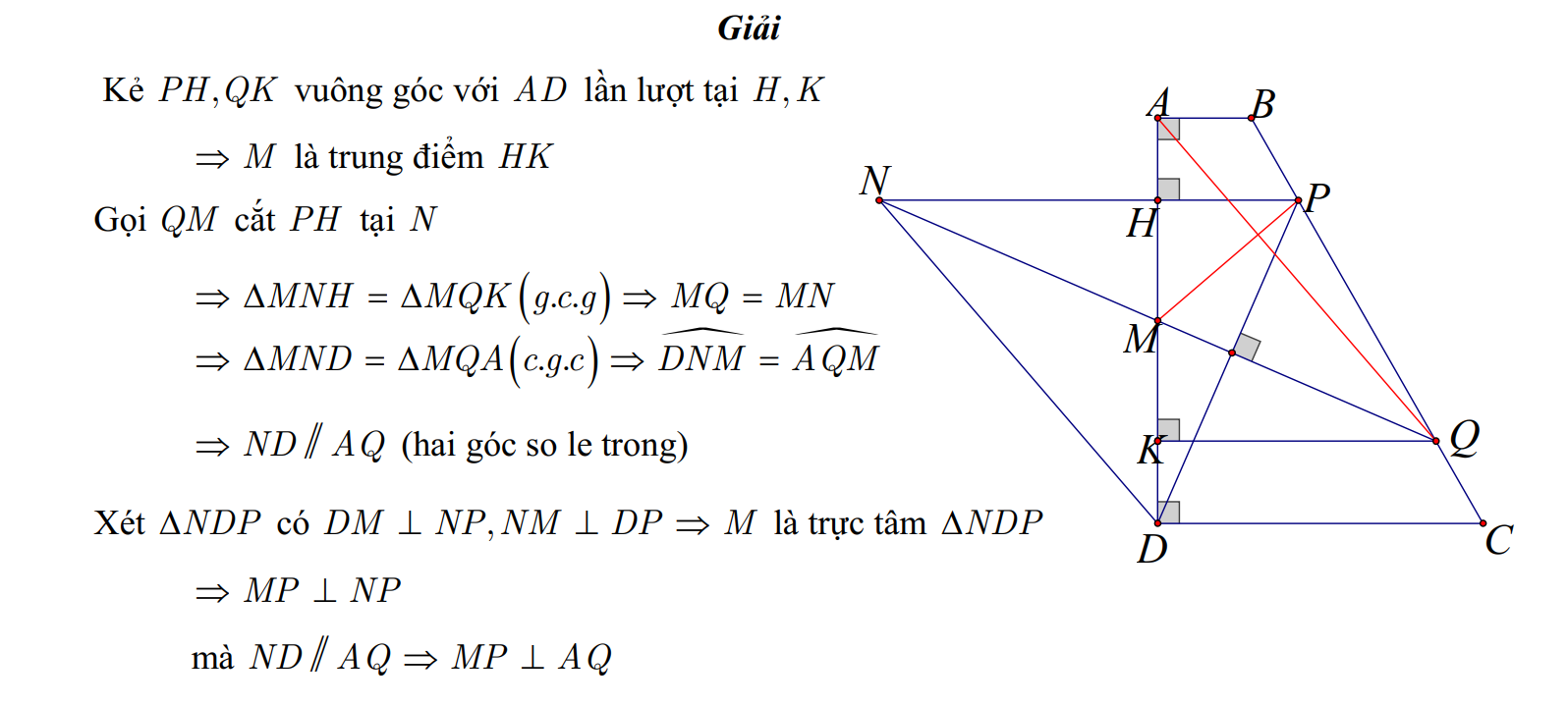
Đúng 0
Bình luận (0)
cho hình vuông ABCD. Lấy M thuộc BC, N thuộc CD sao cho MN=BM+DN. CMR: NA là phân giác DNM
bài 1: Cho hình tam giác ABCD vuông tại A có D là điểm đối xứng của A qua BC, AD cắt BC tại H, vẽ E thuộc HC sao cho HEHB. Vẽ EM vuông góc AC.a) Cmr: ABDE là hình thoib) Cmr: D, E, M thẳng hàngc) Cmr: AE vuông góc DCd) Gọi I là trung điểm EC. Cmr: MH vuông góc MIbài 2: Cho hình thoi ABCD có góc A bằng 600, lấy M thuộc AD, N thuộc DC sao cho AMDN. Tam giác BMN là tam giác gì? Vì sao?
Đọc tiếp
bài 1: Cho hình tam giác ABCD vuông tại A có D là điểm đối xứng của A qua BC, AD cắt BC tại H, vẽ E thuộc HC sao cho HE=HB. Vẽ EM vuông góc AC.
a) Cmr: ABDE là hình thoi
b) Cmr: D, E, M thẳng hàng
c) Cmr: AE vuông góc DC
d) Gọi I là trung điểm EC. Cmr: MH vuông góc MI
bài 2: Cho hình thoi ABCD có góc A bằng 600, lấy M thuộc AD, N thuộc DC sao cho AM=DN. Tam giác BMN là tam giác gì? Vì sao?
cho hình tam giác ABCD ư viết lại đề bài đi bạn
Đúng 0
Bình luận (0)
câu 2
tam giác ABM bằng tam giác DBN (c.g.c) nên BM=BN và ABM=DBN ta có ABM+MBD=60 nên DBN+MBD=60 hay MBN =60 tam giác MBN đều
Đúng 0
Bình luận (0)
Cho hình vuông ABCD cạnh a. Gọi N là điểm thuộc cạnh AD sao cho AN2DN Đường thẳng qua N vuông góc với BN cắt BC tại K. Thể tích khối tròn xoay tạo thành khi quay tứ giác ANKB quanh trục BK là
Đọc tiếp
Cho hình vuông ABCD cạnh a. Gọi N là điểm thuộc cạnh AD sao cho AN=2DN Đường thẳng qua N vuông góc với BN cắt BC tại K. Thể tích khối tròn xoay tạo thành khi quay tứ giác ANKB quanh trục BK là
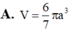
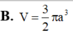
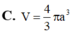
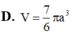
Cho hình vuông ABCD cạnh a. Gọi N là điểm thuộc cạnh AD sao cho AN2DN. Đường thẳng qua N vuông góc với BN cắt BC tại K. Thể tích khối tròn xoay tạo thành khi quay tứ giác ANKB quanh trục BK bằng
Đọc tiếp
Cho hình vuông ABCD cạnh a. Gọi N là điểm thuộc cạnh AD sao cho AN=2DN. Đường thẳng qua N vuông góc với BN cắt BC tại K. Thể tích khối tròn xoay tạo thành khi quay tứ giác ANKB quanh trục BK bằng
![]()
![]()
![]()
![]()
Cho hình vuông ABCD cạnh a. Gọi N là điểm thuộc cạnh AD sao cho AN 2DN. Đường thẳng qua N vuông góc với BN cắt BC tại K. Thể tích khối tròn xoay tạo thành khi quay tứ giác ANKB quanh trục BK là A.
V
6
7
πa
3
B.
V
3
2
πa
3
C.
V
4
3
πa...
Đọc tiếp
Cho hình vuông ABCD cạnh a. Gọi N là điểm thuộc cạnh AD sao cho AN = 2DN. Đường thẳng qua N vuông góc với BN cắt BC tại K. Thể tích khối tròn xoay tạo thành khi quay tứ giác ANKB quanh trục BK là
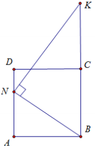
A. V = 6 7 πa 3
B. V = 3 2 πa 3
C. V = 4 3 πa 3
D. V = 7 6 πa 3
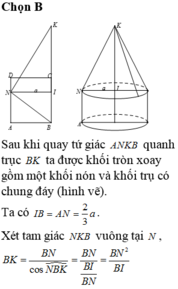
Đáp án D
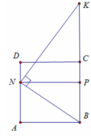
Gọi P là hình chiếu của N xuống BK
Khi quay tứ giác ANPB quanh trục BC ta được khối trụ có thể tích V 1 = πAB 2 . BP = 2 a 3 π 3
Lại có B P = 2 3 a ; N P = a suy ra P K = N P 2 B P = 3 a 2
Khi quay tam giác NKP quanh trục BC ta được khối nón có thể tích do đó V = V 1 + V 2 = 7 6 πa 3
Đúng 0
Bình luận (0)
Cho hình vuông ABCD cạnh a. Gọi N là điểm thuộc cạnh AD sao cho
A
N
2
D
N
.
Đường thẳng qua N vuông góc với BN cắt BC tại K. Thể tích V của khối tròn xoay tạo thành khi quay tứ giác ANKB quanh trục BK là A.
V
7
6
π
a
3
B.
V
14
9
π
a
3...
Đọc tiếp
Cho hình vuông ABCD cạnh a. Gọi N là điểm thuộc cạnh AD sao cho A N = 2 D N . Đường thẳng qua N vuông góc với BN cắt BC tại K. Thể tích V của khối tròn xoay tạo thành khi quay tứ giác ANKB quanh trục BK là
A. V = 7 6 π a 3
B. V = 14 9 π a 3
C. V = 6 7 π a 3
D. V = 9 14 π a 3
Phương pháp:
Công thức tính thể tích của khối trụ có bán kính đáy R và chiều cao h: V = π R 2 h
Công thức tính thể tích của khối nón có bán kính đáy R và chiều cao h: V = 1 3 π R 2 h
Cách giải:
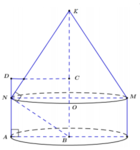
Khi quay tứ giác ANKB quanh trục BK ta được hình trụ có bán kính đáy AB, chiều cao AN và hình nón có bán kính đáy AB, chiều cao K O = B K − A N
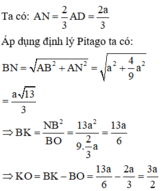
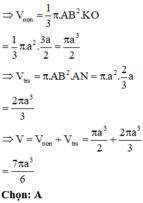
Đúng 0
Bình luận (0)
Cho hình vuông ABCD và các điểm M,N,P,Q lần lượt thuộc các đường thẳng AB,BC,CD,DA sao cho MP vuông góc với NQ .Chứng minh:NQ=MP
Gọi K là giao điểm của MP và NQ
Kẽ MH, QE lần lược vuông góc với DC, BC tại H,E. I, F là giao điểm của QE với MP và MH
Ta có QE //DC
=> MIQ = MPH (góc đồng vị)
MIQ = QNE ( + NQE = 90)
=> MPH = QNE (1)
Xét tam giác QNE và tam giác MPH có
Góc MPH = góc QNE
Góc MHP = góc QEN = 90
MH = QE (cùng bằng cạnh hình vuông)
=> Tam giác QNE = tam giác MPH
=> NQ = PM
Đúng 0
Bình luận (0)
cho hình vuông ABCD, cạnh AB bằng 1 (Đvd). Lấy M thuộc BC, N thuộc DC, sao cho góc MAN lằng 45 độ. CM BM+DN=MN