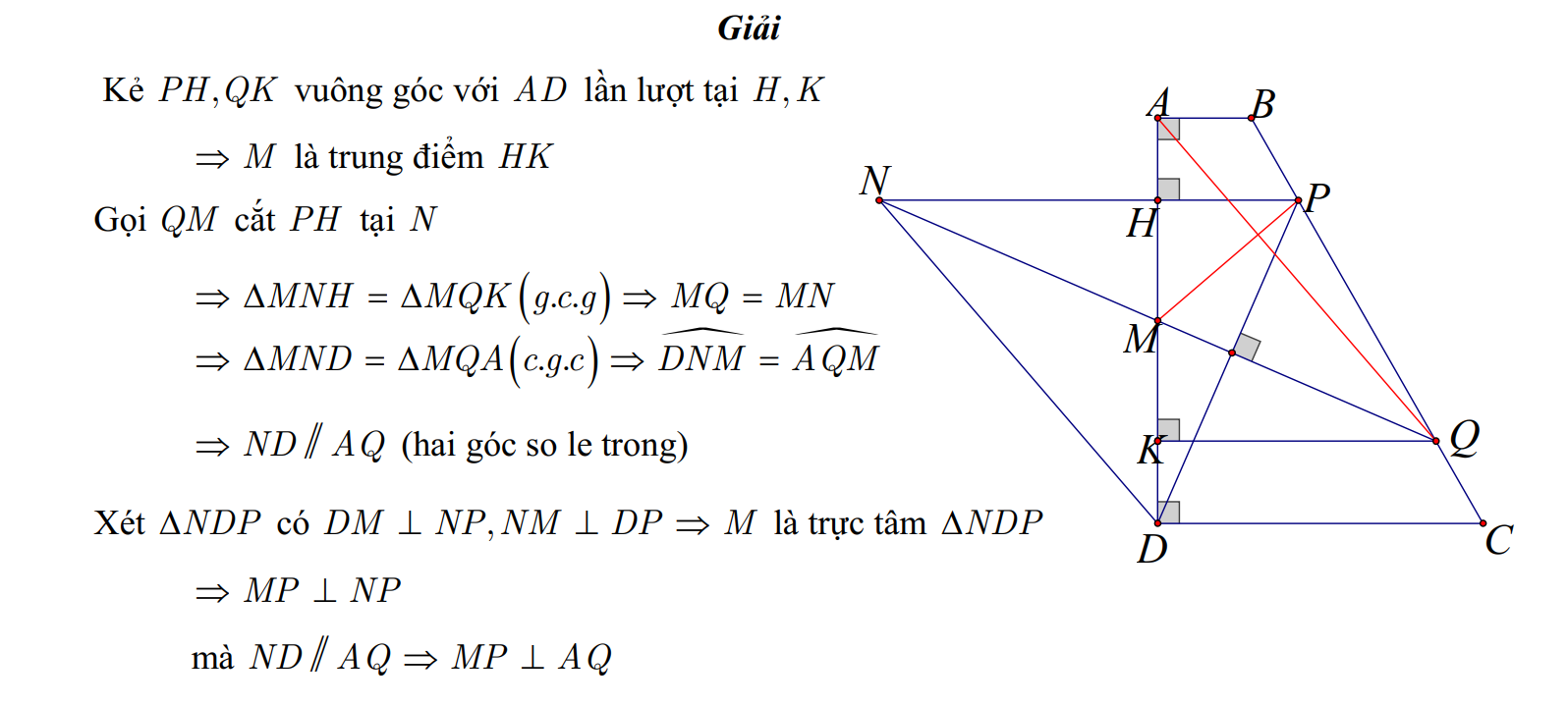
Hình vẽ minh họa, sử dụng tính chất trực tâm của tam giác.
Sử dụng tính chất trực tâm của tam giác .
Cho hình thang ABCD có Ab song song Cd gọi M N P lần lượt là trung điểm của AD AC BC. a Chứng minh MNP thẳng hàng và MP song song với đáy của hình thang b Biết độ dài AB=5 cm,CD=7cm tính độ dài MN NP MP c Có nhận xét gì về độ dài của MP so với tổng độ dài hai đáy AB CD
Bài 1 : Cho hình thang ABCD (AB//CD) .Hai đường phân giác của góc A và B cắt nhau tại điểm K thuộc đáy CD. Chứng minh AD+BC= DC
Bài 2 : Cho ΔABC vuông cân tại A , ở phía ngoài ΔABC , vẽ Δ BCD vuông cân tại B . Tứ giác abcd là hình gì ? Vì sao ?
Cho hình thang ABCD ( AB//CD, AB<CD) hai tia phân giác của góc B và góc C cắt nhau tại I. Qua I kẻ đường thẳng song song với BC cắt AB,CD lần lượt tại E và F
a) Tìm các hình thang
b) Chứng minh rằng tam giác BEI cân
Cho tam giác ABC vuông cân tại A, D thuộc AB, E thuộc AC sao cho AD=AE. Qua D vẽ đoạn thẳng vuông góc BE cắt BC tại K. Qua A vẽ đoạn thẳng vuông góc BE cắt BC tại H. Gọi M là giao điểm của DK và AC. CMR:
a) tam giác BAE = tam giác CAD (cái này mình biết làm rồi)
b) tam giác MDC cân
c) HK = HC
Cho hình thang ABCD (AB//CD), biết AD+BC=AB. Hai tia phân giác của hai góc C và D cắt nhau tại E. Chứng minh rằng 3 điểm A,B,E thẳng hàng.
(Không dùng tính chất hình thang cân và đường trung bình nha!)
Cho hình thang ABCD (AB//CD), biết AD+BC=AB. Hai tia phân giác của hai góc C và D cắt nhau tại E. Chứng minh rằng 3 điểm A,B,E thẳng hàng
(Không dùng tính chất hình thang cân và đường trung bình nha!)
Cho ABCD làh hình thang có BD là phân giác góc D và AE là phân giác góc A với E nằm trên CD. Biết AE//BC và O là giao của AE VÀ BD. Chứng minh:
a) AE vuông góc BD
B) AD//BE, AD=BE
C) E LÀ TRUNG ĐIỂM DC
D) TỨ GIÁC BCEO LÀ HÌNH GÌ
E) GÓC BEC = 80o. TÍNH CÁC GÓC CÒN LẠI CỦA TỨ GIÁC ABCD
Cho hình thang ABCD (AB song song CD, AB > CD). Gọi M, N, P, Q trung điểm AD, BC, AC, BD.
a) Chứng minh M, N, P, Q thẳng hàng
b) Tính MN + PQ biết AB = x, CD = y
c) Nếu MP = PQ = QN. So x với y
cho tam giác ABC vuông tại A (AB<AC). Gọi M là trung điểm BC. Kẻ ME vuông góc AB, MF vuông góc AC
a) Chứng minh: AEMC là hình thang vuông
b) Chứng minh: AEMF là hình chữ nhật
