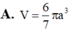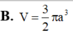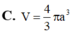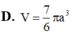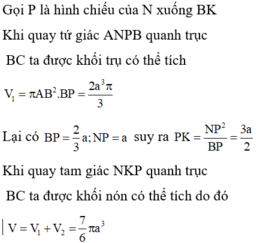Các câu hỏi tương tự
Cho tam giác đều ABC cạnh 1 và hình vuông MNPQ nội tiếp trong tam giác ABC(M
∈
AB, N
∈
AC, P,Q
∈
BC) . Gọi S là phần mặt phẳng chứa các điểm thuộc tam giác ABC nhưng không chứa các điểm thuộc hình vuông MNPQ. Thể tích của vật thể tròn xoay khi quay S quanh trục là đường thẳng qua A vuông góc với BC là:
A
.
810
-
467
3...
Đọc tiếp
Cho tam giác đều ABC cạnh 1 và hình vuông MNPQ nội tiếp trong tam giác ABC(M ∈ AB, N ∈ AC, P,Q ∈ BC) . Gọi S là phần mặt phẳng chứa các điểm thuộc tam giác ABC nhưng không chứa các điểm thuộc hình vuông MNPQ. Thể tích của vật thể tròn xoay khi quay S quanh trục là đường thẳng qua A vuông góc với BC là:
A . 810 - 467 3 24 π
B . 4 3 - 3 96 π
C . 4 3 - 3 96
D . 54 - 31 3 12 π
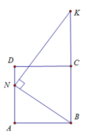
Cho mô hình (như hình vẽ) với tam giác EFB vuông tại B, cạnh FB a ,
E
F
B
^
30
0
và tứ giác ABCD là hình vuông. Tính thể tích V của vật thể tròn xoay được tạo thành khi quay mô hình quanh cạnh AF A.
4
3
a
3
B. ...
Đọc tiếp
Cho mô hình (như hình vẽ) với tam giác EFB vuông tại B, cạnh FB = a , E F B ^ = 30 0 và tứ giác ABCD là hình vuông. Tính thể tích V của vật thể tròn xoay được tạo thành khi quay mô hình quanh cạnh AF
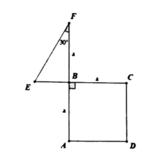
A. 4 3 a 3
B. 10 9 a 3
C. 4 3 πa 3
D. 10 9 πa 3
Cho tam giác OAB vuông tại O, OAOB 4. Lấy một điểm M thuộc cạnh AB và gọi H là hình chiếu của M trên OA. Thể tích của khối tròn xoay được tạo thành khi quay tam giác OMH quanh OA có thể tích lớn nhất bằng A.
256
π
81
B.
81
π
256...
Đọc tiếp
Cho tam giác OAB vuông tại O, OA=OB= 4. Lấy một điểm M thuộc cạnh AB và gọi H là hình chiếu của M trên OA. Thể tích của khối tròn xoay được tạo thành khi quay tam giác OMH quanh OA có thể tích lớn nhất bằng
A. 256 π 81
B. 81 π 256
C. 128 π 81
D. 8 π 3
Cho tam giác ABC vuông tại B có AC2a, BCa khi quay tam giác ABC quay quanh cạnh góc vuông AB thì đường gấp khúc ABC tạo thành một hình nón tròn xoay có diện tích xung quanh bằng
Đọc tiếp
Cho tam giác ABC vuông tại B có AC=2a, BC=a khi quay tam giác ABC quay quanh cạnh góc vuông AB thì đường gấp khúc ABC tạo thành một hình nón tròn xoay có diện tích xung quanh bằng
![]()
![]()
![]()
![]()
Cho tứ diện đểu ABCD cạnh A. Gọi O là tâm của tam giác đểu BCD. M, N lần lượt là trung điểm của AC, AB. Quay hình thang BCMN quanh đường thẳng AO ta được khối tròn xoay có thể tích là bao nhiêu?
Đọc tiếp
Cho tứ diện đểu ABCD cạnh A. Gọi O là tâm của tam giác đểu BCD. M, N lần lượt là trung điểm của AC, AB. Quay hình thang BCMN quanh đường thẳng AO ta được khối tròn xoay có thể tích là bao nhiêu?
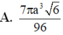
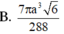
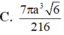
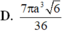
Cho tứ diện ABCD có AD
⊥
(ABC), ABC là tam giác vuông tại B. Biết BCA, ABa
3
, AD3a Quay các tam giác ABC và ABD xung quanh đường thẳng AB ta được 2 khối tròn xoay. Thể tích phần chung của 2 khối tròn xoay đó bằng
Đọc tiếp
Cho tứ diện ABCD có AD ⊥ (ABC), ABC là tam giác vuông tại B. Biết
BC=A, AB=a 3 , AD=3a Quay các tam giác ABC và ABD xung quanh đường thẳng AB ta được 2 khối tròn xoay. Thể tích phần chung của 2 khối tròn xoay đó bằng
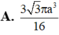
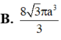
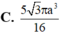
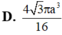
Cho nửa đường tròn đường kính AB 2R và điểm C thay đổi trên nửa đường tròn đó, đặt
α
C
A
B
^
và gọi H là hình chiếu vuông góc của C lên AB. Tìm
α
sao cho thể tích vật thể tròn xoay tạo thành khi quay tam giác ACH quanh trục AB đạt giá trị lớn nhất A.
α
...
Đọc tiếp
Cho nửa đường tròn đường kính AB = 2R và điểm C thay đổi trên nửa đường tròn đó, đặt α = C A B ^ và gọi H là hình chiếu vuông góc của C lên AB. Tìm α sao cho thể tích vật thể tròn xoay tạo thành khi quay tam giác ACH quanh trục AB đạt giá trị lớn nhất
A. α = 60 0
B. α = 45 0
C. α = a r c tan 1 2
D. α = 30 0
Gọi (H) là khối tròn xoay tạo thành khi quay hình quạt OAB (hình vẽ bên) quanh đường thẳng d đi qua O và vuông góc với AB. Biết OAOB2 góc AOB
60
o
Thể tích V của khối tròn xoay (H) gần với giá trị nào sau đây nhất ? A. 1,75 B. 2,25 C. 1,55 D. 3,15
Đọc tiếp
Gọi (H) là khối tròn xoay tạo thành khi quay hình quạt OAB (hình vẽ bên) quanh đường thẳng d đi qua O và vuông góc với AB. Biết OA=OB=2 góc AOB= 60 o Thể tích V của khối tròn xoay (H) gần với giá trị nào sau đây nhất ?
A. 1,75
B. 2,25
C. 1,55
D. 3,15
Cho tứ diện ABCD có cạnh AD vuông góc với mặt phẳng (DBC) và DBC 900. Khi quay các cạnh của tứ diện xung quanh trục là cạnh AB, có bao nhiêu hình nón được tạo thành? A. 1 B. 2 C. 3 D.4
Đọc tiếp
Cho tứ diện ABCD có cạnh AD vuông góc với mặt phẳng (DBC) và DBC = 900. Khi quay các cạnh của tứ diện xung quanh trục là cạnh AB, có bao nhiêu hình nón được tạo thành?
A. 1
B. 2
C. 3
D.4