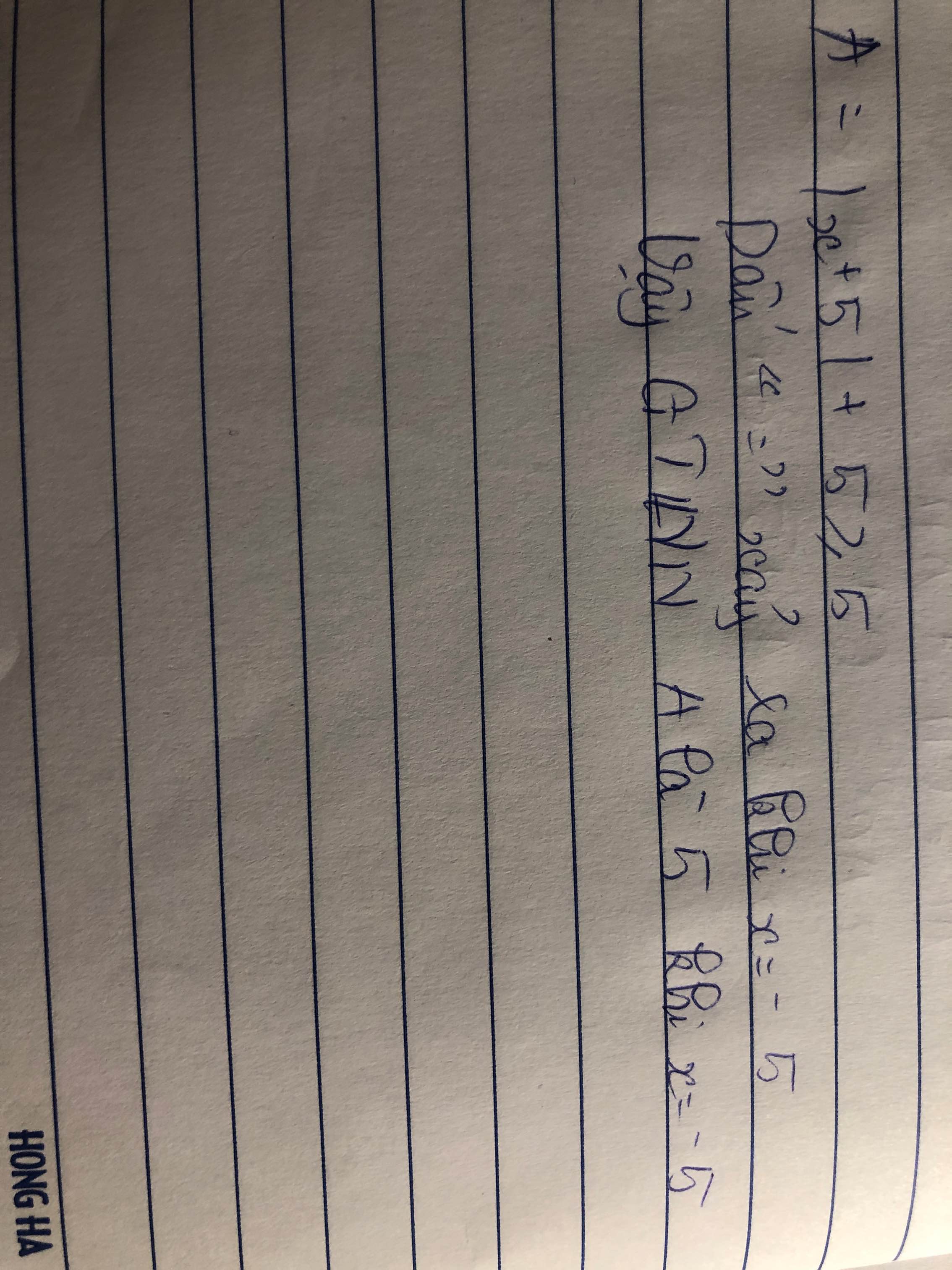Tìm giá trị nhỏ nhất của biểu thức: A= l x-102l + l 2-x l

Những câu hỏi liên quan
a/ Tìm x để biểu thức A = l x-2/3 l -4 đạt giá trị nhỏ nhất
b/ Tìm giá trị lớn nhất của biểu thức: B = 2- l x+5/6 l
c/ Tìm x để biểu thức C = l x l + l x+2 l đạt giá trị nhỏ nhất
giải ra cách làm luôn nhé
ai giải ra cách làm thì mình tick
T/C của gttđ là >= 0 nên
a) GTNN = -4
b) GTLN = 2
c) GTNN = 2
Đúng 0
Bình luận (0)
Tìm giá trị nhỏ nhất của biểu thức sau:
a) I x + 1,5 l
b) l x - 2 l - 9/10
Tìm giá trị lớn nhất của biểu thức sau:
a) -l 2x -1 l
b) 4- l 5x + 3l
\(\left|x+1,5\right|\ge0\forall x\)
Dấu " = " xảy ra khi
| x + 1,5 | = 0
x = -1,5
Vậy MinA = 0 <=> x = -1,5
b)
\(\left|x-2\right|\ge0\forall x\Rightarrow\left|x-2\right|-\frac{9}{10}\ge\frac{9}{10}\forall x\)
Dấu " = " xảy ra khi
| x - 2 | = 0
x = 2
Vậy MinA = \(\frac{9}{10}\)<=> x = 2
Đúng 0
Bình luận (0)
\(-\left|2x-1\right|\le0\forall x\)
Dấu " = " xảy ra khi :
- | 2x - 1 | = 0
=> x = \(\frac{1}{2}\)
Vậy MaxA = 0 <=> x = \(\frac{1}{2}\)
b)
\(-\left|5x-3\right|\le0\forall x\Rightarrow4-\left|5x-3\right|\le4\)
Dấu " = " xảy ra khi :
- | 5x - 3 | = 0
=> x = \(\frac{3}{5}\)
Vậy MaxB = 4 <=> x = \(\frac{3}{5}\)
Study well
Đúng 0
Bình luận (0)
Tìm giá trị nhỏ nhất của biểu thức sau:
a) I x + 1,5 l
b) l x - 2 l - 9/10
Tìm giá trị lớn nhất của biểu thức sau:
a) -l 2x -1 l
b) 4- l 5x + 3l
Tìm giá trị lớn nhất hoặc nhỏ nhất của biểu thức sau :
A =l x + 5 l + 5
Với mọi x ta có :
\(\left|x+5\right|\ge0\)
\(\Leftrightarrow\left|x+5\right|+5\ge0\)
\(\Leftrightarrow A\ge5\)
Dấu "=" xảy ra \(\Leftrightarrow x=-5\)
Vậy..
Đúng 3
Bình luận (1)
Với mọi giá trị của x, ta có:
|x+5|≥0
⇔|x+5|+5≥0
⇔|x+5|+5≥5
Hay A≥5 Với mọi giá trị của x
Để A=5 thì:
|x+5|+5=5
⇔|x+5| =0
⇔x+5 =0
⇔x =\(-5\)
Vậy Amax=5⇔x=-5
Đúng 2
Bình luận (0)
Xem thêm câu trả lời
Tìm giá trị nhỏ nhất của biểu thức D= l x2 +x+3 l + l x2 +x - 6 l
Có D = |x^2 +x+3 | + |x^2 +x-6| = |x^2 +x+3 | + |-x^2 - x + 6 |
Ta co: D = |x^2 +x+3| +|-x^2 -x + 6 | \(\ge\)| x^2 + x + 3 - x^2 - x + 6 |
D \(\ge\)|9 | = 9
D nhỏ nhất chỉ khi D=9
Vậy 9 là giá trị nhỏ nhất của biểu thức D = | x^2 +x+3| + | x^2 + x - 6 |
Đúng 0
Bình luận (0)
\(\left|x^2+x+3\right|+\left|x^2+x-6\right|\)
\(=\left|x^2+x+3-x^2-x+6\right|\)
\(\ge9\)
Đúng 0
Bình luận (0)
tìm giá trị nhỏ nhất của biểu thức: P= l x-2006 l + l x-2007 l +2006
Mik làm tóm tắt:
ta có P=|x-2006|+|2007-x|+2006>=x-2006+2007-x+2006=2007
vậy min P=2007 khi:
x-2006>=0 và 2007-x>=0
=> 2006<=x<=2007
Đúng 0
Bình luận (0)
Tìm số nguyên x để các biểu thức sau đạt giá trị nhỏ nhất.Khi đó giá trị nhỏ nhất là bao nhiêu?
a) A = l x - 5 l
b) B = l 5 + x l
c) C = l - x + 2 l
d) E = l x + 1 l
Tương tụ bài trên
A,B,C,E đạt giá trị nhỏ nhất =0
a)x=5
b)x=-5
c)x=2
d)x=-1
Đúng 0
Bình luận (0)
Tìm giá trị lớn nhất (nhỏ nhất) của biểu thức:
a) A = (x - 1)^2 +1; b) B = x^2 + x^4 - 1/2;
c) C = - (x - 2)^4 -|y - l| + l; d) D = 2/(x-1)^2+1
\(A=\left(x-1\right)^2+1.\\ \left(x-1\right)^2\ge0\forall x\in R.\\ 1>0.\\ \Rightarrow\left(x-1\right)^2+1\ge1\forall x\in R.\\ \Rightarrow A\ge1.\\ \Rightarrow A_{min}=1.\)
\(B=x^2+x^4-\dfrac{1}{2}.\\ x^2+x^4\ge0\forall x\in R.\\ \Leftrightarrow x^2+x^4-\dfrac{1}{2}\ge\dfrac{-1}{2}\forall x\in R.\\ \Rightarrow B\ge\dfrac{-1}{2}.\\ \Rightarrow B_{min}=\dfrac{-1}{2}.\)
\(D=\dfrac{2}{\left(x-1\right)^2}+1.\\ \left(x-1\right)^2\ge0\forall x\in R.\\ \Leftrightarrow\dfrac{2}{\left(x-1\right)^2}\ge0.\\ \Leftrightarrow\dfrac{2}{\left(x-1\right)^2}+1\ge1\forall x\in R.\\ \Rightarrow D\ge1.\\ \Rightarrow D_{min}=1.\)
Đúng 1
Bình luận (1)
Tìm giá trị nhỏ nhất của biểu thức sau l x - 1 l + 2012
Ta có \(\left|x-1\right|\ge0\)
\(\Rightarrow\left|x-1\right|+2012\ge2012\)
Dấu "=" xảy ra \(\Leftrightarrow x=1\)
Vậy Min = 2012 \(\Leftrightarrow x=1\)