Với giá trị nào của m thì hàm số y=\(3x^4-mx^2-24m\) có 3 cực trị

Những câu hỏi liên quan
Cho hàm số
y
x
3
+
3
x
2
+
m
x
+
m
-
2
.
Với giá trị nào của m thì hàm số có 2 điểm cực trị nằm về 2 phía trục tung. A. m 0 B. m 0 C. m 1 D. m 0
Đọc tiếp
Cho hàm số y = x 3 + 3 x 2 + m x + m - 2 . Với giá trị nào của m thì hàm số có 2 điểm cực trị nằm về 2 phía trục tung.
A. m < 0
B. m > 0
C. m = 1
D. m = 0
Đáp án A
Phương pháp:
Hàm số bậc ba có 2 điểm cực trị nằm về 2 phía trục tung khi và chỉ khi phương trình y' = 0 có hai nghiệm trái dấu.
Cách giải:
y = x3 + 3x2 + mx + m - 2 ⇒ y' = 3x2 + 6x + m
Hàm số bậc ba có 2 điểm cực trị nằm về 2 phía trục tung khi và chỉ khi phương trình y' = 0 có hai nghiệm trái dấu ⇔ ac < 0
⇔ 3.m < 0 ⇔ m < 0
Đúng 1
Bình luận (0)
Cho hàm số
y
x
3
+
1
−
2
m
x
2
+
2
2
−
m
x
+
4.
Với giá trị nào của tham số m thì đồ thị hàm số có hai điểm cực trị nằm về hai phía của trục hoành? A.
m...
Đọc tiếp
Cho hàm số y = x 3 + 1 − 2 m x 2 + 2 2 − m x + 4. Với giá trị nào của tham số m thì đồ thị hàm số có hai điểm cực trị nằm về hai phía của trục hoành?
A. m > 2 m < − 2 .
B. − 2 < m < 2.
C. m ≥ 2 − 5 2 ≠ m ≤ − 2 .
D. m > 2 − 5 2 ≠ m < − 2 .
Đáp án D
Điều kiện để hai điểm cực trị nằm về hai phía của trục hoành PT y = 0 có ba nghiệm phân biệt. Xét PT
x 3 + 1 − 2 m x 2 + 2 2 − m x + 4 = 0 ⇔ x 3 + x 2 − 2 m x 2 + 2 m x + 4 x + 4 = 0 ⇔ x + 1 x 2 − 2 m x + 4 = 0
Để PT này có ba nghiệm phân biệt thì
Δ ' = m 2 − 4 > 0 − 1 2 − 2 m . − 1 + 4 ≠ 0 ⇔ m ∈ − ∞ ; − 2 ∪ 2 ; + ∞ m ≠ − 5 2
Đúng 0
Bình luận (0)
Cho hàm số
y
x
2
−
m
x
+
m
2
−
3
m...
Đọc tiếp
Cho hàm số y = x 2 − m x + m 2 − 3 m x − 2 , k h i x ≠ 2 4 m − 1 , k h i x = 2 . Biết rằng m = m 0 thì hàm số liên tục tại x = 2 . Giá trị của P = m 0 4 + 2017 gần với giá trị nào nhất sau đây ?
A. 47,68
B. 42,49
C. 44,92
D. 49,42
Với giá trị nào của m thì hàm số
y
m
x
+
3
x
+
m
đồng biến trên khoảng
2
;
+
∞
A.
m
≥
3
B.
a
3
6
C.
a...
Đọc tiếp
Với giá trị nào của m thì hàm số y = m x + 3 x + m đồng biến trên khoảng 2 ; + ∞
A. m ≥ 3
B. a 3 6
C. a 3 3 2
D. a 3 3 3
Đáp án D
Hàm số đồng biến trên khoảng (2;+∞)
⇔ y’ ≥ 0 ∀ x ϵ D (2;+∞)
Ta có: (-m; +∞) = D (2;+∞)
ð m ≥ -2
Ta có: y’ = m 2 − 3 ( x + m ) 2
ð y’ ≥ 0 ⇔ m ≥ 3 hoặc m ≤ - 3
Vậy tập giá trị m thỏa mãn đề bài là: m ≥ 3 hoặc -2 ≤ m ≤ - 3
Đúng 0
Bình luận (0)
Với giá trị nào của m, hàm số
y
x
3
-
2
x
2
+
m
x
-
1
không có cực trị? A.
m
≥
4
3
B.
m
4
3
C.
m
≤
4
3
D. Không tồn tại
Đọc tiếp
Với giá trị nào của m, hàm số y = x 3 - 2 x 2 + m x - 1 không có cực trị?
A. m ≥ 4 3
B. m < 4 3
C. m ≤ 4 3
D. Không tồn tại
Chọn A
y ' = 3 x 2 - 4 x + m . Hàm số không có cực trị <=> y’=0 vô nghiệm hoặc có nghiệm kép <=> Δ' ≤ 0 <=> 2 2 - 3 m ≤ 0 <=> m ≥ 4 3
Do đó hàm số không có cực trị khi m ≥ 4 3
Đúng 0
Bình luận (0)
cho hàm số y=\(\dfrac{x^2+mx+1}{x+m}\)với m là tham số. với giá trị nào của tham số m thì hàm số đạt cực đại tại x=2?
a. m=-3 b.m=3 c.m=-1 d.m=0
\(y=\dfrac{x^2+mx+1}{x+m}=x+\dfrac{1}{x+m}\)
\(\left\{{}\begin{matrix}y'\left(2\right)=0\\y''\left(2\right)< 0\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}1-\dfrac{1}{\left(2+m\right)^2}=0\\\dfrac{2}{\left(m+2\right)^3}< 0\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}m=-3\\m< -2\end{matrix}\right.\)
Chọn a
Đúng 1
Bình luận (0)
Với các giá trị nào của m thì đồ thị hàm số
y
2
x
2
-
3
x
+
m
x
-
m
không có tiệm cận đứng? A. m 0 D. m 1
Đọc tiếp
Với các giá trị nào của m thì đồ thị hàm số y = 2 x 2 - 3 x + m x - m không có tiệm cận đứng?
A. m = 0
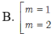
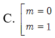
D. m = 1
Bài tập: Với giá trị nào của m thì đồ thị các hàm số :y mx + 3 và y 3x + (5 - m)a) Trùng nhau?
Đọc tiếp
Bài tập: Với giá trị nào của m thì đồ thị các hàm số :
y = mx + 3 và y = 3x + (5 - m)
a) Trùng nhau?
\(\left\{{}\begin{matrix}a=3\Leftrightarrow m=3\\b=5-m=3\Leftrightarrow m=2\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Câu 1 : Tìm tất cả các giá trị của tham số thực m để hàm số \(y=mx^3-2mx^2+\left(m-2\right)x+1\) không có cực trị
Câu 2: Tìm tất cả các giá trị thực của tham số m để hàm số \(y=\left(m-1\right)x^4-2\left(m-3\right)x^2+1\) không có cực đại