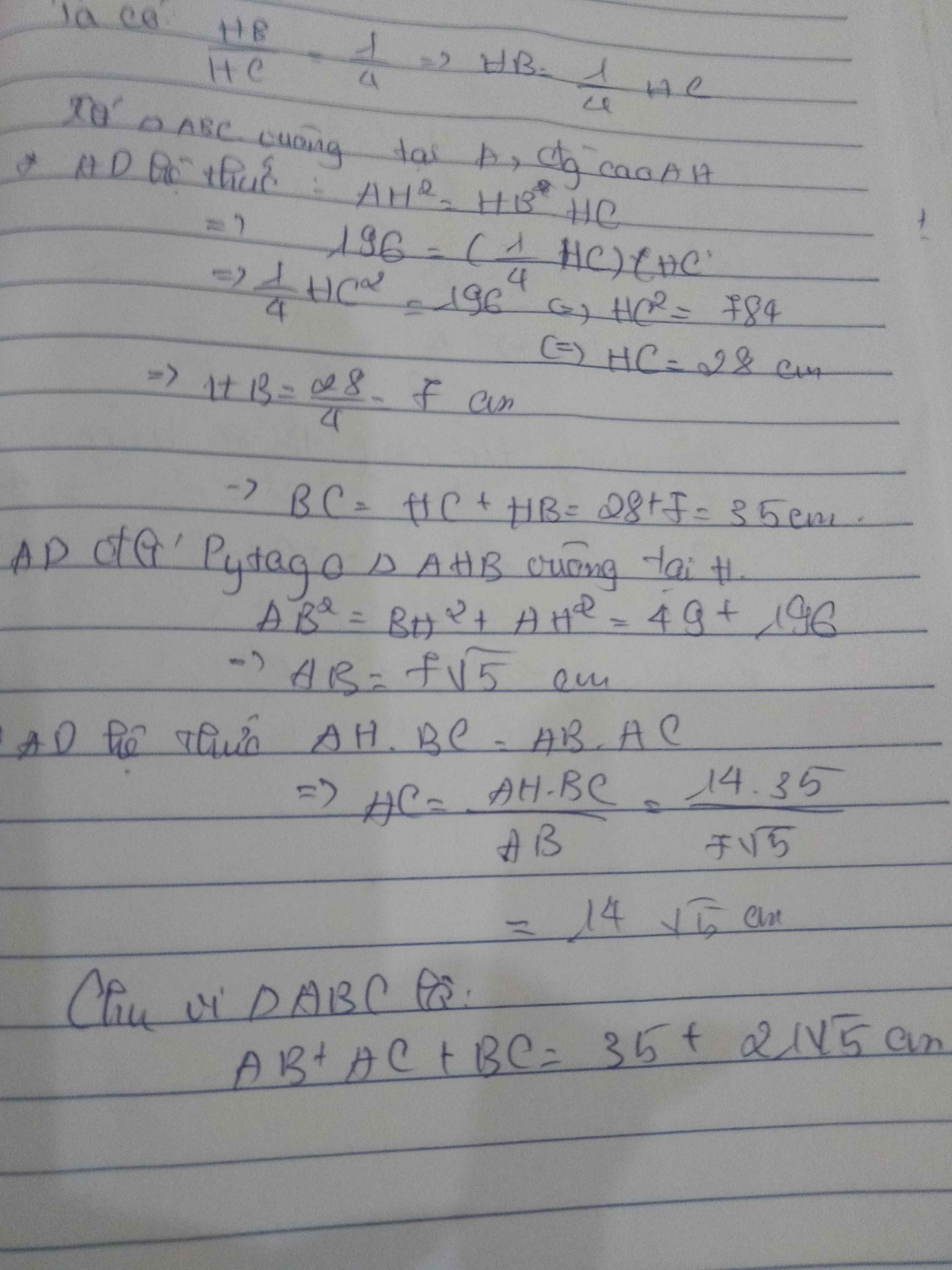Bài 1)Cho ΔABC vuông ở A,đường cao AH.Tính chu vi ΔABC,biết AH =14cm; \(\dfrac{HB}{HC}=\dfrac{1}{4}\)
Bài 2)Cho ΔCDE nhọn,đường cao CH.Gọi M,N theo thứ tự là hình chiếu của H
-GIÚP MÌNH VỚI Ạ- :(((

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A . Kẻ đường cao AH.Tính chu vi tam giác ABC biết AH = 14cm , HB:HC = 1:4 .
Cho tam giác ABC vuông ở A,đường cao AH.Tính Chu vi tam giác ABC biết AH =14cm, \(\frac{HB}{HC}=\frac{1}{4}\)
Cho ΔABC vuông tại A, đường cao AH (H Î BC). Biết tan ABC dfrac{3}{4}, AH 2,4 cm. Tính BH và chu vi ΔABC.
Đọc tiếp
Cho ΔABC vuông tại A, đường cao AH (H Î BC). Biết tan ABC = \(\dfrac{3}{4}\), AH = 2,4 cm. Tính BH và chu vi ΔABC.
Xét ΔAHB vuông tại H có \(tanB=\dfrac{AH}{HB}\)
=>\(\dfrac{2.4}{HB}=\dfrac{3}{4}\)
=>\(HB=2.4\cdot\dfrac{4}{3}=3,2\left(cm\right)\)
ΔABH vuông tại H
=>\(HA^2+HB^2=AB^2\)
=>\(AB^2=3,2^2+2,4^2=16\)
=>\(AB=\sqrt{16}=4\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AB^2=BH\cdot BC\)
=>\(BC=\dfrac{4^2}{3,2}=5\left(cm\right)\)
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2=5^2-4^2=9\)
=>\(AC=\sqrt{9}=3\left(cm\right)\)
Chu vi tam giác ABC là:
3+4+5=12(cm)
Đúng 1
Bình luận (0)
BÀI 1: Cho ΔABC vuông tại A. Biết BC=a, đường cao AH. Chứng minh rằng:
a, AH = a . sinB . cosB
b, BH = a . cos2B
c, CH = a . sin2B
BÀI 2: Cho ΔABC vuông ở A, đường cao AH, đường phân giác trong AD chia cạnh huyền thành hai đoạn tỉ lệ 1 : 3. Tính tỉ số của hai đoạn thẳng BH và CH.
GIÚP MÌNH VỚI Ạ! MÌNH CẦN GẤP
Bài 2:
Xét ΔABC có AD là đường phân giác ứng với cạnh BC
nên \(\dfrac{AB}{AC}=\dfrac{BD}{CD}\)
\(\Leftrightarrow\dfrac{AB}{AC}=\dfrac{1}{3}\)
\(\Leftrightarrow\dfrac{BH}{CH}=\dfrac{1}{9}\)
Đúng 0
Bình luận (3)
Xét ΔABC có AD là đường phân giác ứng với cạnh BC
nên \(\dfrac{AB}{AC}=\dfrac{BD}{CD}\)
⇔ \(\dfrac{AB}{AC}=\dfrac{1}{3}\)
\(\Leftrightarrow\dfrac{AB^2}{AC^2}=\dfrac{1}{9}\)
\(\Leftrightarrow\dfrac{BC.BH}{BC.CH}=\dfrac{1}{9}\)
\(\Leftrightarrow\dfrac{BH}{CH}=\dfrac{1}{9}\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A . Kẻ đường cao AH.Tính chu vi tam giác ABC biết AH = 14cm , HB:HC = 1:4 .
Xét tam giác ABC vuông tại A, đường cao AH
Ta có : \(\frac{HB}{HC}=\frac{1}{4}\Rightarrow HB=\frac{1}{4}HC\)
* Áp dụng hệ thức : \(AH^2=BH.HC=\left(\frac{1}{4}HC\right)HC=\frac{1}{4}HC^2\)
\(\Rightarrow196=\frac{1}{4}HC^2\Leftrightarrow HC^2=784\Leftrightarrow HC=28\)cm
=> HB = 28/4 = 7 cm
=> BC = HB + HC = 28 + 7 = 35 cm
Áp dụng định lí Pytago tam giác AHB vuông tại H
\(AB^2=BH^2+AH^2=49+196=245\Rightarrow AB=7\sqrt{5}\)cm
* Áp dụng hệ thức : \(AH.BC=AB.AC\Rightarrow AC=\frac{AH.BC}{AB}=14\sqrt{5}\)cm
Chu vi tam giác ABC là : \(P_{ABC}=AB+AC+BC=35+21\sqrt{5}\)cm
Cho ΔABC vuông tại A, đường cao AH, trung tuyến AM. Biết AM-AH=7cm và chu vi của tam giác ABC là 72cm. Tính SΔABC
Cho tam giác ABC vuông ở A, đường cao AH. Tính chu vi của tam giác ABC , biết AH=14cm, HB/HC = 1/4

tham khảo của đỗ chí dũng câu hỏi của chi khánh
Cho ΔABC vuông cân ở A , đường cao AH = 2cm
a) C/m ΔABC∼ΔHCA
b) Tính AB , HC
a) Xét ΔABC vuông tại A và ΔHCA vuông tại H có
\(\widehat{C}\) chung
Do đó: ΔABC\(\sim\)ΔHCA(g-g)
b) Ta có: ΔABC\(\sim\)ΔHCA(cmt)
nên \(\dfrac{AB}{HC}=\dfrac{AC}{AH}=\dfrac{BC}{CA}\)
\(\Leftrightarrow\dfrac{AB}{AC}=\dfrac{HC}{AH}=1\)
\(\Leftrightarrow HC=AH=2\left(cm\right)\)
Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC(ΔABC vuông cân tại A)
AH chung
Do đó: ΔAHB=ΔAHC(cạnh huyền-cạnh góc vuông)
Suy ra: HB=HC(hai cạnh tương ứng)
mà HC=2cm(cmt)
nên HB=2cm
Áp dụng định lí Pytago vào ΔAHB vuông tại H, ta được:
\(AB^2=AH^2+HB^2\)
\(\Leftrightarrow AB^2=8\)
hay \(AB=2\sqrt{2}\left(cm\right)\)
Đúng 0
Bình luận (0)
ΔABC vuông ở A , đường cao AH
a) C/m ΔABC ∼ ΔHBA
b) Biết AB =8cm , AC=15cm . Tính BC
c) Tính HB , HC
a.Xét tam giác ABC và tam giác HBA có:
^B chung
^BAC = ^BHA = 90
=> tam giác ABC ~ tam giác HBA (g.g)
b. Áp dụng đl Pytago cho tam giác ABC vuông tại A:
BC2=AB2+AC2=82+152=289
=>BC=17cm
c.tam giác ABC ~ tam giác HBA
=> AB/HB=BC/BA
=>HB=AB2/BC=82/17=64/17 cm
=>HC=BC-HB=225/17
Đúng 1
Bình luận (0)
* Cho ΔABC vuông tại A, biết AC= 12cm, BC=15cm
a. Giải tam giác ABC
b. Tính độ dài đường cao AH, đường phân giác AD của ΔABC
* Cho ΔABC có 3 góc nhọn, kẻ đường cao AH.
a. CM: sinA+cos A>1
b. CM: BC=AH. (cotgB+cotgC)
c. Biết AH=6cm, góc B=\(60^0\), góc C=\(45^0\). Tính diện tích ΔABC
Bài 2:
b: \(AH\cdot\left(\cot\widehat{B}+\cot\widehat{C}\right)\)
\(=AH\cdot\left(\dfrac{BH}{AH}+\dfrac{CH}{AH}\right)\)
\(=AH\cdot\dfrac{BC}{AH}=BC\)
Đúng 0
Bình luận (0)