Cho tam giác ABC vuông tại A, đường cao AH. Tính độ dài BH,CH,AB,AC biết AH=12cm và BC=26cm

Những câu hỏi liên quan
1. Cho tam giác ABC vuông tại A(AB<AC) có đường cao AH. Biết BC = 25cm, AH = 12cm. Tính AB, AC, BH, CH
2. Cho tam giác ABC vuồng tại A, đường cao AH. Biết AB = 15cm, HC = 16cm. Tính AC, BC, AH, BH
Cho tam giác ABC vuông tại A, đường cao AH
a, Cho biết AB = 3cm, BC = 5cm. Tính độ dài đoạn thẳng BH,CH, AH và AC
b, Cho biết AH = 60cm, CH = 144cm. Tính độ dài đoạn thẳng AB, AC, BC, và BH
a, HB = 1,8cm; CH = 3,2cm; AH = 2,4cm; AC = 4cm
b, AB = 65cm; AC = 156cm; BC = 169cm; BH = 25cm
c, AB = 5cm; BC = 13cm; BH = 25/13cm; CH = 144/13cm
Đúng 0
Bình luận (0)
câu 1:Cho tam giác ABC,vuông tại A,đường cáo AH(H thuộc BC).Biết AB12CM,Ac5cm.tính BH,CHCâu 2:cho tam giác ABC vuông tại A,đường cáo AH(H thuộc BC).Biết AB18cm,BH6cm.tính đô dài các cạnh AB,ACCâu 3:cho tam giac abc vuông tại a,biết ab-3cm,ac4cm,a.tinh bcb:kẻ đường cao ah,tính bhCâu 4:cho tam giác ABC Vuông tại A,biết ab4cm,đường cao ah2cm.Tính các góc và các cạnh còn lại của tam giác
Đọc tiếp
câu 1:Cho tam giác ABC,vuông tại A,đường cáo AH(H thuộc BC).Biết AB=12CM,Ac=5cm.tính BH,CH
Câu 2:cho tam giác ABC vuông tại A,đường cáo AH(H thuộc BC).Biết AB=18cm,BH=6cm.tính đô dài các cạnh AB,AC
Câu 3:cho tam giac abc vuông tại a,biết ab-3cm,ac=4cm,
a.tinh bc
b:kẻ đường cao ah,tính bh
Câu 4:cho tam giác ABC Vuông tại A,biết ab=4cm,đường cao ah=2cm.Tính các góc và các cạnh còn lại của tam giác
Câu 1:
Áp dụng đ/lí pytago vào tam giác ABC vuông tại A CÓ:AB^2+AB^2=BC^2
Hay: 12^2+5^2=169=BC^2
=> BC=13cm
ÁP dụng hệ thức ta có:
+) AB^2=BH.BC
Hay: BH=AB^2:BC=144:13 =144/13(cm)
Ta có CH=BC-BH=13-144/13=25/13(cm)
Đúng 0
Bình luận (0)
Bạn chỉ cần áp dụng hệ thức lượng là đc rồi o0o
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A , đường cao AH . Chứng minh rằng 1/AH^2=1/AB^2+1/ac^2
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho hình bên là tam giác ABC vuông tại A, đường cao AH. Cho biết AB = 5cm, AC = 12cm. Tinh độ dài các đoạn thẳng BC, AH, BH và CH.
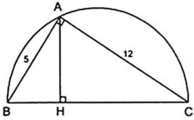
Áp dụng định lý Py – ta – go vào tam giác ABC vuông tại A ta có:
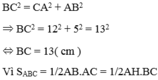
⇒ AH.BC = AB.AC
Hay 12.5 = AH.13 ⇒ AH = 60/13 ( cm )
Từ câu a ta có: Δ BHA ∼ Δ BAC ⇒ BH/BA = BA/BC hay BH/5 = 5/13 ⇔ BH = 25/13( cm )
Do đó: CH = BC - BH = 13 - 25/13 = 144/13( cm )
Đúng 0
Bình luận (0)
cho tam giác vuông tại A,đường cao AH
a,cho biết AB = 3cm,BC = 5cm. Tính độ dài các đoạn thẳng BH,CH,AH và AC
b,cho biết AH = 60cm,CH = 144cm. Tính độ dài các đoạn thẳng AB,AC,BC và BH
c,cho biết AC = 12cm,AH = \(\dfrac{60}{13}cm.\) Tính độ dài các đoạn thẳng AB,BC<BH và CH
a: AC=căn 5^2-3^2=4cm
AH=3*4/5=2,4cm
BH=3^2/5=1,8cm
CH=5-1,8=3,2cm
b: \(BH=\sqrt{60^2:144}=5\left(cm\right)\)
BC=144+5=149cm
\(AB=\sqrt{5\cdot149}=\sqrt{745}\left(cm\right)\)
\(AC=\sqrt{144\cdot149}=12\sqrt{149}\left(cm\right)\)
c: \(HC=\sqrt{AC^2-AH^2}=\dfrac{144}{13}\left(cm\right)\)
\(BH=\dfrac{AH^2}{HC}=\dfrac{25}{13}cm\)
BC=BH+CH=13(cm)
AB=căn 13^2-12^2=5cm
Đúng 0
Bình luận (0)
a
Áo dụng đl pytago vào tam giác ABC vuông tại A:
\(AC=\sqrt{BC^2-AB^2}=\sqrt{5^2-3^2}=4\left(cm\right)\)
Theo hệ thức lượng vào tam giác ABC vuông tại A có đường cao AH:
\(AB^2=BH.BC\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{3^2}{5}=1,8\left(cm\right)\)
\(CH=BC-BH=5-1,8=3,2\left(cm\right)\)
\(AH.BC=AB.AC\Rightarrow AH=\dfrac{3.4}{5}=2,4\left(cm\right)\)
b
Áp dụng đl pytago vào tam giác AHC vuông tại H có:
\(AC=\sqrt{AH^2+HC^2}=\sqrt{60^2+144^2}=156\left(cm\right)\)
Theo hệ thức lượng vào tam giác ABC vuông tại A, đường cao AH có:
\(AC^2=HC.BC\Rightarrow BC=\dfrac{AC^2}{HC}=\dfrac{156^2}{144}=169\left(cm\right)\)
\(BH=BC-HC=169-144=25\left(cm\right)\)
\(AB^2=BH.BC\Rightarrow AB=\sqrt{25.169}=65\left(cm\right)\)
c
Áp dụng đl pytago vào tam giác AHC vuông tại H:
\(HC=\sqrt{AC^2-AH^2}=\sqrt{12^2-\left(\dfrac{60}{13}\right)^2}=\dfrac{144}{13}\approx11,08\left(cm\right)\)
Theo hệ thức lượng vào tam giác ABC đường cao AH có:
\(AH^2=HB.HC\Rightarrow HB=\dfrac{AH^2}{HC}=\dfrac{\left(\dfrac{60}{13}\right)^2}{\dfrac{144}{13}}=\dfrac{25}{13}\approx1,92\left(cm\right)\)
\(BC=HB+HC=\dfrac{25}{13}+\dfrac{144}{13}=13\left(cm\right)\)
\(AB^2=HB.BC\Rightarrow AB=\sqrt{HB.HC}=\sqrt{\dfrac{144}{13}.\dfrac{25}{13}}=\dfrac{60}{13}\approx4,62\left(cm\right)\)
Đúng 1
Bình luận (0)
Giúp em với:
Tam giác ABC vuông tại A đường cao AH biết AH=12cm BC=26cm tính AB,AC,BC,CH
Hình tự vẽ nhé
ta có :
AB^2=BC*BH
<=> BH=AB^2/BC
<=> BH=12^2/ 13= BẠN TỰ TÍNH NHÉ TẠI K CÓ MT :">
Ta có : BC=BH+HC
HAY HC=BC-BH=13-BH
Ta cũng có AH^2=BH*HC
<=> AH=BH⋅HC−−−−−−−−√BH⋅HC= BẠN TỰ TÍNH =))
Áp dụng định lí py-ta-go vào tam giác vuông ABC ta có :
AB^2+AC^2=BC^2
Hay 12^2+AC^2=13^2
<=> AC=132−122−−−−−−−−√132−122= ( BẠN TỰ TÍNH NHÉ TẠI KHÔNG CÓ MÁY TÍNH =))
chân thành sorry =))
Đúng 0
Bình luận (0)
cho tam giác ABC vuông tại A, AH là đường cao. Tính lần lượt độ dài các đoạn thẳng BH, CH, AH, AC nếu biết :
1) AB = 6 cm, BC = 8cm
2) AB = 12cm, BC = 13cm
3) AB = 20cm, BC = 25cm
Lời giải:
1) Xét tam giác $BHA$ và $BAC$ có:
$\widehat{B}$ chung
$\widehat{BHA}=\widehat{BAC}=90^0$
$\Rightarrow \triangle BHA\sim \triangle BAC$ (g.g)
$\Rightarrow \frac{BH}{BA}=\frac{BA}{BC}$
$\Rightarrow BH=\frac{BA^2}{BC}=\frac{6^2}{8}=4,5$ (cm)
$CH=BC-BH=8-4,5=3,5$ (cm)
Áp dụng định lý Pitago:
$AC=\sqrt{BC^2-AB^2}=\sqrt{8^2-6^2}=2\sqrt{7}$ (cm)
$AH=\frac{AB.AC}{BC}=\frac{6.2\sqrt{7}}{8}=\frac{3\sqrt{7}}{2}$ (cm)
2. 3. Những phần này bạn làm tương tự như phần 1.
Đúng 0
Bình luận (0)
1, Cho tam giác ABC vuông tại A,đường cao AH
a, Cho biêt AB=3cm,BC=5cm.Tính độ dài đoạn thẳng BH,CH,AH và AC
b,Cho biết AH=60cm,CH=144cm.Tính độ dài đoạn thẳng AB,AC,BC và BH
2, Cho tam giác ABC vuông tại A, đường cao AH
Cho biết \(\dfrac{AB}{AC}\)=\(\dfrac{5}{6}\) và BC=122cm.Tính độ dài các đoạn thẳng BH,CH
Bài 2:
Ta có: \(\dfrac{AB}{AC}=\dfrac{5}{6}\)
\(\Leftrightarrow\dfrac{HB}{HC}=\dfrac{25}{36}\)
\(\Leftrightarrow HB=\dfrac{25}{36}HC\)
Ta có: HB+HC=BC
\(\Leftrightarrow HC\cdot\dfrac{61}{36}=122\)
\(\Leftrightarrow HC=72\left(cm\right)\)
hay HB=50(cm)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH. Biết AB: 12cm, AH:7,2 cm. tính AC BC BH CH
Áp dụng HTL:
\(\dfrac{1}{AH^2}=\dfrac{1}{51,84}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}=\dfrac{1}{144}+\dfrac{1}{AC^2}\\ \Rightarrow\dfrac{1}{AC^2}=\dfrac{1}{81}\Rightarrow AC=9\left(cm\right)\)
Áp dụng PTG \(BC=\sqrt{BA^2+AC^2}=15\left(cm\right)\)
Áp dụng HTL:
\(\left\{{}\begin{matrix}BH=\dfrac{AB^2}{BC}=9,6\left(cm\right)\\CH=\dfrac{AC^2}{BC}=5,4\left(cm\right)\end{matrix}\right.\)
Đúng 2
Bình luận (0)
cho tam giác ABC vuông tại A (AB<AC) có đường cao AH và AH =12cm, BC=25cm
tính BH,CH,AB,AC
Đặt BH=x; CH=y(x<y)
Theo đề, ta có:
x+y=25 và xy=12^2=144
=>x,y là các nghiệm của phương trình:
a^2-25a+144=0
=>a=9; a=16
=>BH=9cm; CH=16cm
AH=căn 9*16=12cm
AB=căn 9*25=15cm
AC=căn 16*25=20cm
Đúng 0
Bình luận (0)





















