tách tam thức bậc 2 hoặc bậc 3 (lớp 8): x^3 + x + 2

Những câu hỏi liên quan
Có cách nào để tách đa thức bậc 3 trở lên thành nhân tử cho lớp 8 mà không cần dùng máy tính không?ví dụ như câu này: x^4+x^3+6.x^2+5.x+5 hoặc câu này x^3.y^3+x^2.y^2+4
Phân tích đa thức thành nhân tử bằng cách tách hạng tử bậc nhất: x^2 - 11x + 8
= [x2 - 2.x.\(\frac{11}{2}\) + \(\left(\frac{11}{2}\right)^2\)] - \(\frac{121}{4}\)+ 8 = (x - \(\frac{11}{2}\))2 - \(\frac{89}{4}\) = (x - \(\frac{11}{2}\))2 - \(\left(\frac{\sqrt{89}}{2}\right)^2\)
= \(\left(x-\frac{11}{2}-\frac{\sqrt{89}}{2}\right).\left(x-\frac{11}{2}+\frac{\sqrt{89}}{2}\right)\)= \(\left(x-\frac{11+\sqrt{89}}{2}\right).\left(x+\frac{\sqrt{89}-11}{2}\right)\)
Đúng 0
Bình luận (0)
Biểu thức nào sau đây là tam thức bậc hai? Nếu là tam thức bậc hai, hãy xét dấu của nó tại \(x = 1\).
a) \(f\left( x \right) = 2{x^2} + x - 1\);
b) \(g\left( x \right) = - {x^4} + 2{x^2} + 1\)
c) \(h\left( x \right) = - {x^2} + \sqrt 2 .x - 3\)
a) Biểu thức \(f\left( x \right) = 2{x^2} + x - 1\) là một tam thức bậc hai
\(f\left( 1 \right) = {2.1^2} + 1 - 1 = 2 > 0\) nên \(f\left( x \right)\) dương tại \(x = 1\)
b) Biểu thức \(g\left( x \right) = - {x^4} + 2{x^2} + 1\) không phải là một tam thức bậc hai
c) Biểu thức \(h\left( x \right) = - {x^2} + \sqrt 2 .x - 3\) là một tam thức bậc hai
\(h\left( 1 \right) = - {1^2} + \sqrt 2 .1 - 3 = \sqrt 2 - 4 < 0\) nên \(h\left( x \right)\) âm tại \(x = 1\)
Đúng 0
Bình luận (0)
Đơn thức \( - {2^3}{x^2}y{z^3}\) có:
A. Hệ số -2, bậc 8
B. Hệ số \( - {2^3}\), bậc 5
C. Hệ số -1, bậc 9
D. Hệ số \( - {2^3}\), bậc 6
Đơn thức \( - {2^3}{x^2}y{z^3}\) có hệ số là \( - {2^3}\), bậc là 2+1+3=6.
Chọn D.
Đúng 0
Bình luận (0)
Bài 1: xét dấu tam thức bậc hai
1.f(x)= -1/2 x^2
2.f(x)=x^2-2x-1
3.v=-x^2-4x+1
4.v=x^2+x+1
5.v=-x^2+4x+6
6.y= căn bặc hai 2x^2
7.y=((1-căn bậc hai 2)x^2-2x-1
8.v=2(x+3)^2-5
9.v= trừ căn bậc hai 2^2+4x
Đa thức nào sau đây là tam thức bậc hai?
a) \(4{x^2} + 3x + 1\)
b) \({x^3} + 3{x^2} - 1\)
c) \(2{x^2} + 4x - 1\)
a) Đa thức \(4{x^2} + 3x + 1\) là tam thức bậc hai
b) Đa thức \({x^3} + 3{x^2} - 1\) không là tam thức bậc hai
c) Đa thức \(2{x^2} + 4x - 1\) là tam thức bậc hai
Đúng 0
Bình luận (0)
Xét dấu các tam thức bậc hai sau:
a) \( - 3{x^2} + x - \sqrt 2 \)
b) \({x^2} + 8x + 16\)
c) \( - 2{x^2} + 7x - 3\)
a) \(f(x) = - 3{x^2} + x - \sqrt 2 \)có \(\Delta = 1 - 12\sqrt 2 < 0\)và a=-3<0 nên \(f(x) < 0\)với mọi \(x \in \mathbb{R}\)
b) \(g(x) = {x^2} + 8x + 16\) có \(\Delta = 0\)và a=1>0 nên g(x) có nghiệm kép \(x = - 4\) và g(x) >0 với mọi \(x \ne - 4\)
c) \(h(x) = - 2{x^2} + 7x - 3\) có \(\Delta = 25\)>0 và a=-2<0 và có 2 nghiệm phân biệt \({x_1} = \frac{1}{2};{x_2} = 3\)
Do đó ta có bảng xét dấu h(x)

Suy ra h(x) <0 với mọi \(x \in \left( { - \infty ;\frac{1}{2}} \right) \cup \left( {3; + \infty } \right)\) và h(x)>0 với mọi \(x \in \left( {\frac{1}{2};3} \right)\)
Đúng 0
Bình luận (0)
Tìm x để các bt có nghĩa vd : căn bậc hai của 7x+3 = 7x+3 lớn hơn hoặc bằng x tương đương x lớn hơn hoặc bằng -3 phần 7
Căn bậc hai của 1 phần x-3
Căn bậc hai của -3 phần 2-x
a) Quan sát Hình 21 và cho biết dấu của tam thức bậc hai fleft( x right) {x^2} + 3x + 2 tùy theo các khoảng của x.b) Quan sát Hình 22 và cho biết dấu của tam thức bậc hai fleft( x right) - {x^2} + 4x - 3 tùy theo các khoảng của x.c) Từ đó rút ra mối liên hệ về dấu của tam thức bậc hai fleft( x right) a{x^2} + bx + cleft( {a ne 0} right) với dấu của hệ số tùy theo các khoảng của x trong trường hợp Delta 0.
Đọc tiếp
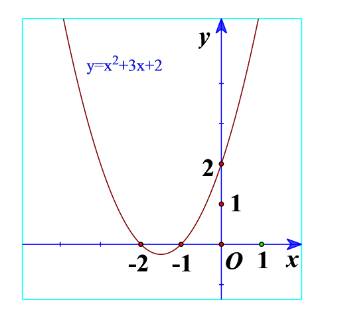
a) Quan sát Hình 21 và cho biết dấu của tam thức bậc hai \(f\left( x \right) = {x^2} + 3x + 2\) tùy theo các khoảng của x.
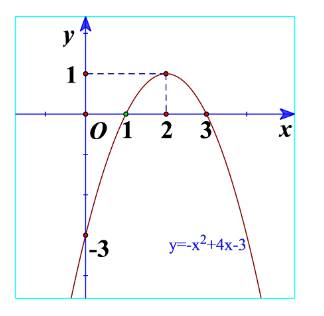
b) Quan sát Hình 22 và cho biết dấu của tam thức bậc hai \(f\left( x \right) = - {x^2} + 4x - 3\) tùy theo các khoảng của x.
c) Từ đó rút ra mối liên hệ về dấu của tam thức bậc hai \(f\left( x \right) = a{x^2} + bx + c\left( {a \ne 0} \right)\) với dấu của hệ số tùy theo các khoảng của x trong trường hợp \(\Delta > 0\).
a) Ta thấy trên \(\left( { - \infty ; - 2} \right)\): Đồ thị nằm trên trục hoành
=> \(f\left( x \right) = {x^2} + 3x + 2 > 0\)\(\forall x \in \left( { - \infty ; - 2} \right)\)
Trên \(\left( { - 2; - 1} \right)\): Đồ thị nằm dưới trục hoành
=> \(f\left( x \right) = {x^2} + 3x + 2 < 0\)\(\forall x \in \left( { - 2; - 1} \right)\)
Trên \(\left( { - 1; + \infty } \right)\): Đồ thị nằm trên trục hoành
=> \(f\left( x \right) = {x^2} + 3x + 2 > 0\)\(\forall x \in \left( { - 1; + \infty } \right)\)
b)
Trên \(\left( { - \infty ;1} \right)\): Đồ thị nằm dưới trục hoành
=> \(f\left( x \right) = - {x^2} + 4x - 3 < 0\)\(\forall x \in \left( { - \infty ;1} \right)\)
Trên \(\left( {1;3} \right)\): Đồ thị nằm trên trục hoành
=> \(f\left( x \right) = - {x^2} + 4x - 3 > 0\)\(\forall x \in \left( {1;3} \right)\)
Trên \(\left( {3; + \infty } \right)\): Đồ thị nằm dưới trục hoành
=> \(f\left( x \right) = - {x^2} + 4x - 3 < 0\)\(\forall x \in \left( {3; + \infty } \right)\)
c) Nếu \(\Delta > 0\) thì \(f\left( x \right)\) cùng dấu vưới hệ số a với mọi x thuộc các khoảng \(\left( { - \infty ;{x_1}} \right)\) và \(\left( {{x_2}; + \infty } \right)\); \(f\left( x \right)\) trái dấu với hệ số a với mọi x thuộc khoảng \(\left( {{x_1};{x_2}} \right)\), trong đó \({x_1},{x_2}\) là hai nghiệm của \(f\left( x \right)\) và \({x_1} < {x_2}\).
Đúng 0
Bình luận (0)










