Cho tam giác có 3 đường cao, độ dài lần lượt là 5cm, 12cm, 13cm. Hỏi tam giác đó có vuông không?

Những câu hỏi liên quan
Bài Tính Chất Ba Đường Trung Trực Của Tam Giác
Câu hỏi
-cho tam giác ABC(h. 53) hãy chỉ ra đường trung trực của tam giac đó
- hãy vé tam giác ABC có độ dài các cạnh lần lượt là 5cm, 12cm, 13cm. Từ đó vẽ các đường trung trực của tam giác này
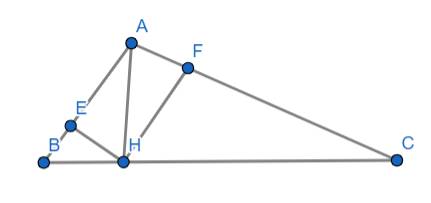
Cho tam giác ABC có AB = 5cm AC= 12cm , BC= 13cm C/minh tam giác ABC vuông b) Tính độ dài đường cao AH c) Gọi E, F lần lượt là hình chiếu của H trên AB và AC C/minh góc AFE = góc ABC Mình cần gấp ạ
a) Ta có: \(BC=13cm\Rightarrow BC^2=13^2cm=169cm\)
Xét: \(AB^2+AC^2=5^2+12^2=25+144=169=13^2=BC^2\)
Vậy tam giác ABC vuông tại A có cạnh huyền BC
b) Áp dụng định lý thích hai cạnh góc vuông tà tích giữa cạnh huyền và đường cao ta có:
\(AH\cdot BC=AB\cdot AC\)
\(\Rightarrow AH=\dfrac{AB\cdot AC}{BC}=\dfrac{12\cdot5}{13}\approx4,6\left(cm\right)\)
c) Xét ΔAHB vuông tại H có đường cao HE ta có:
\(\Rightarrow AH^2=AE\cdot AB\) (1)
Xét ΔAHC vuông tại H có đường cao HF ta có:
\(\Rightarrow AH^2=AF\cdot AC\) (2)
Từ (1) và (2)
\(\Rightarrow AB\cdot AE=AC\cdot AF\)
\(\Rightarrow\dfrac{AB}{AF}=\dfrac{AC}{AE}\) (3)
Dựa vào (3)
Ta suy ra: \(\Delta AEF\sim\Delta ABC\)
\(\Rightarrow\widehat{AEF}=\widehat{ABC}\) (đpcm)
Đúng 3
Bình luận (0)
a: Xét ΔÂBC có BC^2=AB^2+AC^2
nên ΔABC vuông tại A
b: AH=AB*AC/BC=60/13(cm)
c: ΔAHB vuông tại H có HE là đường cao
nên AE*AB=AH^2
ΔAHC vuông tại H có HF là đường cao
nên AF*AC=AH^2
=>AE*AB=AF*AC
=>AE/AC=AF/AB
=>ΔAEF đồng dạng với ΔACB
=>góc AFE=góc ABC
Đúng 1
Bình luận (0)
Tam giác ABC có vuông không, nếu như ba đường cao có độ dài lần lượt là
a) 3cm, 4cm, 5cm
b) 12cm, 15cm, 20cm
a) ta có : 52=32+42
=> tam giác ABC vuông ( theo định lý Pi-ta-go đảo )
b) ta có : 202<122+152
=> tam giác ABC không vuông
Đúng 0
Bình luận (0)
a) cho tam giác MND có MN=5cm, MD=13cm, DN=12cm. Hỏi tam giác MND có phải là∆ vuông không? Vì sao?
Xem chi tiết
Ta có: \(MN^2+DN^2=5^2+12^2=169\); \(MD^2=13^2=169\)
\(\Rightarrow MD^2=MN^2+ND^2\).
Theo hệ quả của định lý Pytago ta có \(\Delta MND\) vuông tại \(N\).
Đúng 3
Bình luận (0)
Một tam giác có độ dài ba cạnh là 12cm, 5cm, 13cm. Diện tích tam giác đó là
A. 60 c m 2
B. 30 c m 2
C. 45 c m 2
D. 32 , 5 c m 2
Ta có: 52 + 122 = 169; 132 = 169
=> 52 + 122 = 132
Do đó đây tam giác đã cho là tam giác vuông có hai cạnh góc vuông là 5cm và 12cm.
Diện tích của nó là: 1 2 .12.5 = 30 (cm2)
Đáp án cần chọn là: B
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A,AB=12cm,BC=13cm. Gọi M, N lần lượt là trung điểm của AB và BC
a) Chứng minh MN là đường trung bình của tam giác. Từ đó chứng minh MN vuông với AB
b) Tính độ dài MN
a) Xét tam giác ABC có:
M là trung điểm AB(gt)
N là trung điểm BC(gt)
=> MN là đường trung bình
=> MN//AC
Mà AC⊥AB(tam giác ABC vuông tại A)
=> MN⊥AB(từ vuông góc đến song song)
b) Xét tam giác ABC vuông tại A:
\(BC^2=AB^2+AC^2\left(pytago\right)\)
\(\Rightarrow AC^2=BC^2-AB^2=13^2-12^2=25\Rightarrow AC=5\left(cm\right)\)
Ta có: MN là đường trung bình tam giác ABC
\(\Rightarrow MN=\dfrac{1}{2}AC=\dfrac{1}{2}.5=2,5\left(cm\right)\)
Đúng 2
Bình luận (0)
Cho tam giác KQP có KQ=5cm; KP=12cm; QP=13cm. Đường cao KH.
a) Chứng minh tam giác KQP vuông
b)Tính góc Q; góc P và độ dài KH; PH
c)Lấy điểm O bất kì trên cạnh QP. Gọi hình chiếu của O trên KQ, KP lần lượt là A và B. Chứng minh AB=KO và tìm vị trí của O để diện tích tứ giác KBOA lớn nhất
cho tam giác abc có ab=5cm, ac=12cm,bc=13cm
a)chứng minh tam giác ABC vuông tại A và tính độ dài đường cao AH
b)kẻ HE vuong AB tại E , HF vuông AC tại F . Chứng minhAE.AB=AF>AC
c)chứng minh tam giác AFE và tanm giác ABC đồng dạng
B1: đường cao của một tam giác vuông chia cạnh huyền thành 2 đoạn thẳng có độ dài là 3 và 4. hãy tính các cạnh góc vuông của tam giác này
B2:Cho tam giác ABC có A=90 độ đường cao AH . Biết AB:AC=3:4, BC=15 . Tính BH và HC
B3: Cho tam giác ABC có đường cao AH , trung tuyến AM. Biết AH =12cm, AM=13cm. Tính HB , HC.
B1: Gọi Tam giác ABC vuông tại A có AH là đ/cao chia cạnh huyền thành 2 đoạn HB và HC
AH2=HB x HC =3x4=12
AH=căn 12 r tính mấy cạnh kia đi
B2: Ta có AB/3=AC/4 suy ra AB = 3AC/4
Thế vào cong thức Pytago Tam giác ABC tính máy cái kia
Đúng 0
Bình luận (0)
Oh 2015 tuong ms dang chu :v
Đúng 0
Bình luận (0)





















