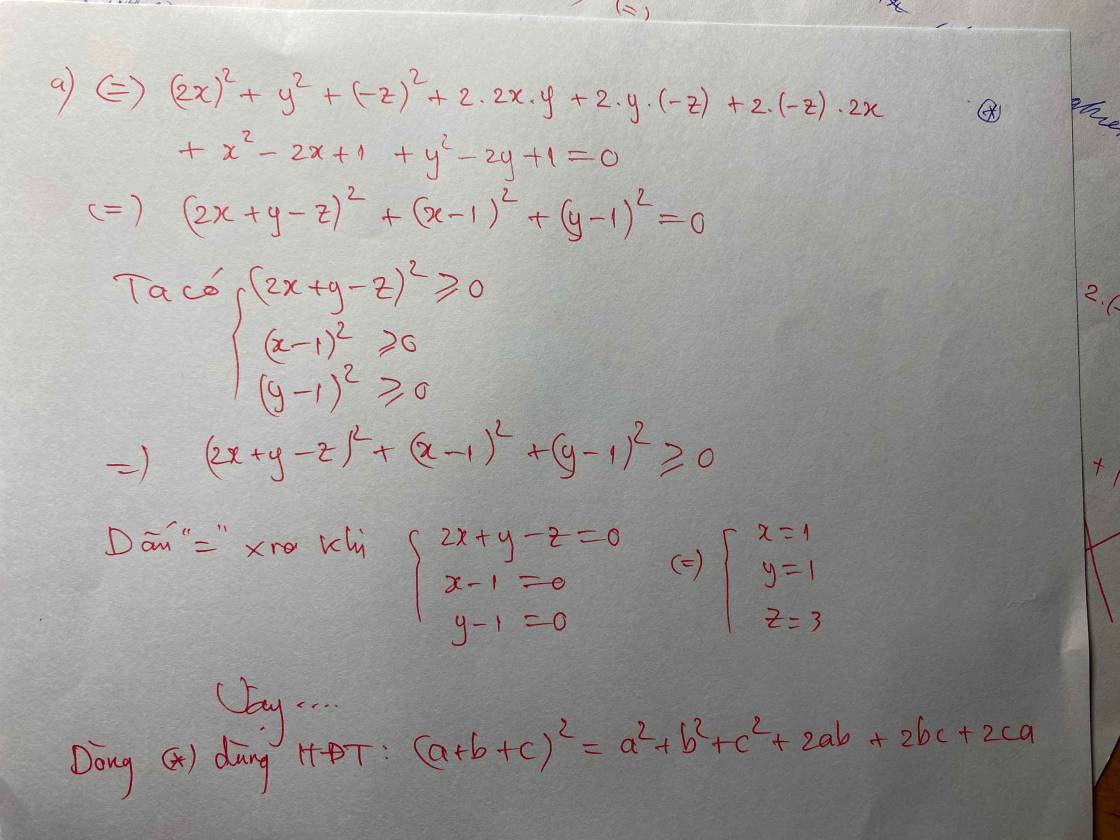
Học tốt nha bn ! ( dòng * ko cần ghi vào đâu bn đây là nháp giở của mik )

Anh/ chị viết rõ đề bằng công thức toán được không ạ?

Vd : 1/2(2x+2y+z)^2 là \(\frac{1}{2\left(2x+2y+z\right)^2}\) hay sao?

\(P=8x^3+8y^3+\frac{z^3}{\left(2x+2y+2z\right)\left(4xy+2yz+2zx\right)}\) đúng ko ạ?

ai giúp vs

(x-2y-2)²+(y-6)² =39-2A

A=< 39/2, max A là 39/2 khi x =14 và y =6

Lời giải:
$4x^2+2y^2+2z^2-4xy-4xz+2yz-6y-10z+34=0$

$(4x^2+y^2+z^2-4xy-4xz+2yz)+y^2+z^2-6y-10z+34=0$

$(2x-y-z)^2+(y^2-6y+9)+(z^2-10z+25)=0$
$(2x-y-z)^2+(y-3)^2+(z-5)^2=0$

Vì $(2x-y-z)^2\geq 0; (y-3)^2\geq 0; (z-5)^2\geq 0$ với mọi $x,y,z$

Do đó để tổng của chúng bằng $0$ thì bản thân mỗi số đó bằng $0$

$\Rightarrow 2x-y-z=y-3=z-5=0$

$\Rightarrow y=3; z=5; x=4$

Khi đó:
$P=0^{2023}+(-1)^{2025}+(5-4)^{2027}=0$

Đặt x = -2y + k (k \(\inℤ\))

Ta có x² + 8y² + 4xy - 2x - 4y = 4

<=> (-2y + k)² + 8y² + 4y(-2y + k) - 2(-2y + k) - 4y = 4

<=> k² + 4y² - 2k = 4

<=> (k - 1)² + (2y)² = 5 (*) 

Dễ thấy (2y)² \(⋮4\) (**)

Với y,k \(\inℤ\) kết hợp (*) ; (**) ta được 

\(\left\{{}\begin{matrix}\left(k-1\right)^2=1\\\left(2y\right)^2=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}k=0\\k=2\end{matrix}\right.\\y=\pm1\end{matrix}\right.\) 

Vậy (k,y) = (0;1) ; (0;-1) ; (2;1) ; (2;-1) 

mà x = k - 2y nên các cặp (x;y) thỏa là (-2;1) ; (2;-1) ; (0;1) ; (4;-1)  

\(\Leftrightarrow x^2+4y^2+4xy-2\left(x+2y\right)+1=5-4y^2\)

\(\Leftrightarrow\left(x+2y+1\right)^2=5-4y^2\)

TH1 : \(4y^2=0\)

Pt \(\Leftrightarrow\left(x+2y+1\right)^2=5\)Mà 5 không là số chính phương.

=> Không có số nguyên x nào thỏa mãn.

TH2 : \(4y^2>0\)

Do \(\left(x+2y+1\right)^2\ge0\Rightarrow5\ge4y^2\)

Mà y nguyên

=> \(4y^{2}=4\)

=> y ∈ {1 ; -1}

Với y = 1

=> x + 3 = 1

=> x = -2 (tm)Với y = -1

=> x - 1 = 1

=> x = 2 (tm)Vậy..