cho tam giác abc. hãy xác định điểm M sao cho : vetor MA +MB + MC =vector 0
cho tam giác ABC : a)tìm các điểm M và N sao cho vector MA - vector MB + vector MC = vector 0 và 2 vector NA + vector NB + vector NC = vector 0
a: \(\overrightarrow{MA}-\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow{0}\)
=>\(\overrightarrow{BM}+\overrightarrow{MA}+\overrightarrow{MC}=\overrightarrow{0}\)
=>\(\overrightarrow{BA}+\overrightarrow{MC}=\overrightarrow{0}\)
=>\(\overrightarrow{BA}=\overrightarrow{CM}\)
=>BAMC là hình bình hành
=>M là điểm thỏa mãn BAMC là hình bình hành
Gọi K là trung điểm của BC
\(2\overrightarrow{NA}+\overrightarrow{NB}+\overrightarrow{NC}=\overrightarrow{0}\)
=>\(2\overrightarrow{NA}+2\overrightarrow{NK}=\overrightarrow{0}\)
=>\(\overrightarrow{NA}+\overrightarrow{NK}=\overrightarrow{0}\)
=>N là trung điểm của AK
Cho tam giác ABC Xác định vị trí điểm M sao cho vecto MA - vecto MB + vecto MC = vecto 0
Ta thấy \(\overrightarrow{MA}-\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{MA}+\overrightarrow{BM}+\overrightarrow{MC}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{BA}=\overrightarrow{CM}\)
Như vậy, điểm M chính là đỉnh thứ tư của hình bình hành ABCM.
Đố: Cho tam giác ABC. Em hãy tô màu để xác định phần bên trong của tam giác gồm các điểm M sao cho:
MA < MB < MC.
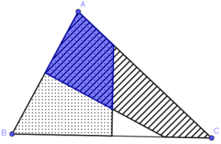
Áp dụng kết quả bài 70 (chương III – SGK) ta có:
MA < MB khi M thuộc nửa mặt phẳng chứa điểm A bờ là đường trung trực của AB (phần gạch chéo)
MB < MC khi M thuộc nửa mặt phẳng chứa điểm B bờ là đường trung trực của BC (phần được chấm chấm).
(Cách chứng minh xem lại bài 70).
Phần giao của hai nửa mặt phẳng trên là phần hình chứa điểm M thỏa mãn MA < MB < MC (phần hình được tô màu xanh).
cho tam giác ABC. Hãy xác định điểm M thỏa mãn điều kiện :vecto MA -vecto Mb + vecto MC=0
cho tam giác ABC : a)tìm các điểm M và N sao cho vector MA - vector MB + vector MC = vector 0 và 2 vector NA + vector NB + vector NC = vector 0
b) với các điểm M,N ở câu a), tìm các số p và q sao cho vector MN = p nhân vector AB + q nhân vector AC
a: 
b: \(\overrightarrow{MN}=\overrightarrow{MA}+\overrightarrow{AN}\)
\(=\overrightarrow{CB}+\dfrac{1}{2}\cdot\overrightarrow{AK}\)
\(=\overrightarrow{CA}+\overrightarrow{AB}+\dfrac{1}{2}\cdot\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)\)
\(=-\overrightarrow{AC}+\overrightarrow{AB}+\dfrac{1}{4}\overrightarrow{AB}+\dfrac{1}{4}\overrightarrow{AC}\)
\(=\dfrac{5}{4}\cdot\overrightarrow{AB}-\dfrac{3}{4}\cdot\overrightarrow{AC}\)
Cho tam giác ABC có M thỏa mãn điều kiện M A → + M B → + M C → = 0 → . Xác định vị trí điểm M
A. M là điểm thứ tư của hình bình hành ACBM
B.M là trung điểm của đoạn thẳng AB
C.M trùng C
D.M là trọng tâm tam giác ABC
Đáp án D
Gọi G là trọng tâm tam giác ABC.
Ta có ![]()
Cho tam giác ABC có M thỏa mãn điều kiện
M A → + M B → + M C → = 0 → Xác định vị trí điểm M
A. M là điểm thứ tư của hình bình hành ACBM
B.M là trung điểm của đoạn thẳng AB
C.M trùng C
D.M là trọng tâm tam giác ABC
Gọi G là trọng tâm tam giác ABC.
Ta có
![]()
Chọn D.
Cho tam giác ABC có ba góc nhọn. Xác định vị trí của điểm M trong tam giác sao cho MA + MB + MC nhỏ nhất.
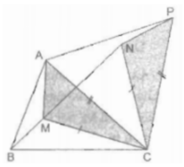
Trong ∆ ABC ta lấy điểm M. Nối MA, MB, MC.
Ta cần làm xuất hiện tổng MA + MB + MC sau đó tìm điều kiện để tổng đó nhỏ nhất.
Lấy MC làm cạnh dựng trên nửa mặt phẳng bờ BC chứa điểm A tam giác đều MCN. Suy ra: CM = MN.
Lấy AC làm cạnh dựng trên nửa mặt phẳng bờ AC không chứa điểm B tam giác đều APC. Khi đó, CA = CP
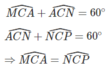
Xét ∆ AMC và ∆ PNC:
CM = CN (vì ΔMCN đều)
CA = CP (vì ΔAPC đều)
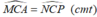
Suy ra: ∆ AMC = ∆ PNC (c.g.c)
⇒ PN = AM
MA + MB + MC = NP + MB + MN
Ta có ∆ ABC cho trước nên điểm P cố định nên BM + MN + NP ngắn nhất khi 4 điểm B, M, N, P thẳng hàng.

Đố :
Cho tam giác ABC. Em hãy tô mầu để xác định phần bên trong của tam giác gồm các điểm M sao cho :
MA < MB < MC
(Hướng dẫn: Trước tiên tô màu để xác định các điểm M ở trong tam giác mà MA < MB lần thứ hai là MB < MC. Phần trong tam giác được tô mầu hai lần là phải tìm)

Điểm M nằm trong ∆ABC sao cho AM < BM thì tô phần tam giác ABC thuộc nửa mp bờ là trung trực của đoạn AB có chứa điểm A.
-Điểm M nằm trong ABC sao cho MB
- Điểm M nằm trong ΔABC sao cho MA < MB thì tô phần ΔABC thuộc nửa mặt phẳng bờ là trung trực của đoạn AB có chứa điểm A (phần màu đỏ).
- Điểm M nằm trong ΔABC sao cho MB < MC thì tô phần ΔABC thuộc nửa mặt phẳng bờ là đường trung trực của đoạn BC có chứa B (phần màu xanh). Phần tam giác được tô hai lần (đỏ và xanh) là phần chứa điểm M thỏa: MA < MB < MC.
- Điểm M nằm trong ΔABC sao cho MA < MB thì tô phần ΔABC thuộc nửa mặt phẳng bờ là trung trực của đoạn AB có chứa điểm A (phần màu đỏ).
- Điểm M nằm trong ΔABC sao cho MB < MC thì tô phần ΔABC thuộc nửa mặt phẳng bờ là đường trung trực của đoạn BC có chứa B (phần màu xanh). Phần tam giác được tô hai lần (đỏ và xanh) là phần chứa điểm M thỏa: MA < MB < MC.