cho 2 góc xOy và mIn
sao cho Ox // Im ; Oy // In
a) Chứng minh: góc xOy = góc mIn ( nếu cùng nhọn hay cùng tù )
b) góc xOy + góc mIn = 180 độ ( nếu cùng nhọn hay cùng tù )
Giải giúp mình với nha ^_^
cho góc nhọn xOy . Từ I trong góc xOy kẻ In // Ox và Im // Oy. chứng minh góc xOy=góc nIm
có nx vẽ mối quan hệ giữa 2 cạnh của góc đó
Cho góc xOy khác góc bẹt . M là điểm nằm trong góc xOy . Vẽ MI vuông góc với Ox ( I thuộc Ox ) , MH vuông góc với Oy ( H thuộc Oy ) . Trên tia đối của tia IM lấy điểm A sao cho IA = IM , trên tia đối của tia HM lấy điểm B sao cho HB = HM . CMR OA = OB
xét tam giác OMI và tam giác OAI có : OI chung
IM = IA (gt)
^OIM = ^OIA = 90
=> tam giác OMI = tam giác OAI (2cgv)
=> OM = OA (1)
xét tam giác OHM và tam giác OHB có : OH chung
HB = HM (gt)
^OHB = ^OHM = 90
=> tam giác OHM = tam giác OHB (2cgv)
=> OB = OM và (1)
=> OA = OB
Hình bạn tự kẻ nha , mình ghi bải giải
Xét tam giác OAM có : OI là đường cao(Vì OI vuông góc với AM )
OI là trung tuyến(Vì I là trung điểm AM)
=> Tam giác OAM cân tại O (vì có đường cao vừa là đường trung tuyến)
=> OA = OM (1)
Xét tam giác OBM có : OH là đường cao(Vì OH vuông góc với BM)
OH là trung tuyến(Vì H là trung điểm BM)
=> Tam giác OBM cân tại O(Vì có đường cao vừa là đường trung tuyến)
=> OM = OB (2)
Từ (1) và (2) suy ra OA = OB (vì cùng bằng OM)
Học Tốt
Cho góc xOy có số đo bằng 60 độ. Lấy điểm I trên tia Ox, trên nửa mặt phẳng bờ Ox chứa tia Oy kẻ Im song song với Oy, và In vuông góc với Ox. Số đo góc mIn
Ta có xoy+olm =180 độ suy ra oml = 180- 60= 120 độ
Trên cùng nủa mf bờ ox chứa oy ta có oln+nom =120 =olm
suy ra nom=120-90 =30 độ
Cho góc nhọn xOy,Oz là tia phân giác của góc đó.Trên tia Ox lấy điểm A,trên tia Oy lấy điểm B sao cho OA=OB.Gọi I là giao điểm của Oz và AB.a) CM:∆OIA=∆OIB.CM:Oz vuông góc với AB.b)Từ I kẻ IN vuông góc Ox và IM vuông góc Oy(N thuộc Ox,M thuộc Oy).CM: IM=IN.c)CM:góc BIM=góc AIN.d)CM:MN song song AB
a) Xét △OIA và △OIB có:
OA = OB
\(\widehat{AOI}=\widehat{BOI}\)
OI : cạnh chung
Suy ra △OIA = △OIB (c.g.c)
Ta lại có △OAB có OA = OB nên △OAB là tam giác cân tại O
Vì Oz là đường phân giác của △OAB nên Oz đồng thời là đường
cao của △OAB.
Suy ra \(Oz\perp AB\)(*)
b)△INO có \(\widehat{OIN}+\widehat{N}+\widehat{ION}\)= 180o (tổng ba góc của một tam giác)
△IMO có \(\widehat{OI}M+\widehat{M}+\widehat{IOM}\)= 180o (tổng ba góc của một tam giác)
Mà \(\widehat{ION}=\widehat{IOM};\widehat{N}=\widehat{M}=90^o\)
Nên \(\widehat{OIN}=\widehat{OIM}\)
Xét △IMO và △INO có :
\(\widehat{OIN}=\widehat{OIM}\)
IO : cạnh chung
\(\widehat{ION}=\widehat{IOM}\)
Suy ra △IMO = △INO (g.c.g) (**)
Nên IM = IN
c) Từ (*) suy ra \(\widehat{BIO}=\widehat{AIO}=90^o\)
Mặc khác \(\widehat{BIO}=\widehat{BIM}+\widehat{MIO}\)
\(\widehat{AIO}=\widehat{AIN}+\widehat{NIO}\)
Mà\(\widehat{MIO}=\widehat{NIO}\)(từ (**) suy ra)
Nên \(\widehat{BIM}=\widehat{AIN}\)
d)Gọi T là giao điểm của MN và tia Oz
Từ (*) suy ra △AIO vuông tại I và △OTN vuông tại T.
nên \(\widehat{AIO}=\widehat{NTO}=90^o\)
△AIO có: \(\widehat{A}+\widehat{AIO}+\widehat{IOA}\) = 180o(tổng ba góc của một tam giác)
△OTN có: \(\widehat{TNO}+\widehat{NTO}+\widehat{TON}\) = 180o(tổng ba góc của một tam giác)
Mà \(\widehat{AIO}=\widehat{NTO}=90^o\)và \(\widehat{IOA}=\widehat{TON}\)
Suy ra \(\widehat{A}=\widehat{TNO}\)
Nên MN//AB
Bài 2 : cho góc xOy khác góc bẹt . M là điểm nằm trong góc xOy . Vẽ MI vuông góc với Ox tại I , MH vuông góc với Oy tại H . Trên tia đối của tia IM lấy điểm A sao cho IA = IM, trên tia đối của tia HM lấy B sao cho HB = HM . Chứng minh rằng OA = OB
cho góc nhọn xOy. Vẽ tia phân giác Oz của góc xOy. Lấy hai điểm M và N lần lượt thuộc tia Ox và tia Oy sao cho OM=ON. Lấy điểm I bất kỳ thuộc tia Oz. Chứng minh rằng A) tam giác OIM = tam giác OIN B) Góc OIM = Góc OIN C) IM = IN
`a,` Xét Tam giác `OIM` và Tam giác `OIN` có:
`OM = ON (g``t)`
\(\widehat{MOI}=\widehat{NOI}\) `(` tia phân giác \(\widehat{xOy}\) `)`
`OI` chung
`=>` Tam giác `OIM =` Tam giác `OIN (c-g-c)`
`b,` Vì Tam giác `OIM =` Tam giác `OIN (a)`
`->` \(\widehat{OIM}=\widehat{OIN}\) `( 2` góc tương ứng `)`
`c,` Vì Tam giác `OIM =` Tam giác `OIN (a)`
`-> IM = IN (2` cạnh tương ứng `)`
`\color{blue}\text {#DuyNam}`
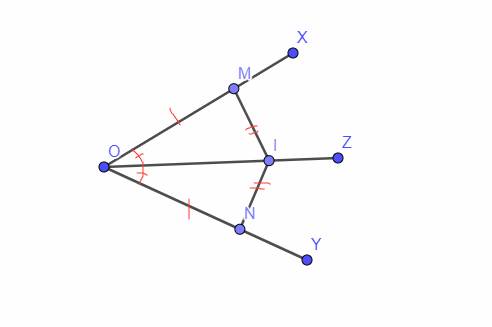
cho 2 góc xOy và tIm sao cho Ox song song It
và Oy song song với Im. Gọi Oz là tia phân giác của xOy
In là tia phân giác của tIm.
C/m Oz vuông góc với In hoặc Oz//In
(hai trường hợp có vẽ hình ai nhanh mình tíck)
cho góc nhọn xoy oz là tia phân giác của góc đó. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA = OB. Gọi I là giao điểm của Oz và AB
a, Chứng minh: tam giác OIA = tam giác OIB. Chứng minh Oz và AB
b, Từ I kẻ IN vuông góc Ox và IM vuông góc Oy ( N thuộc Ox, M thuộc Oy). Chứng minh IM = IN
c) Chứng minh: Góc BIM = Góc AIN
d) Chứng minh: MN // AB
a: Xét ΔOIA và ΔOIB có
OA=OB
\(\widehat{AOI}=\widehat{BOI}\)
OI chung
Do đó: ΔOIA=ΔOIB
b: Xét ΔONI vuông tại N và ΔOMI vuông tại M có
OI chung
\(\widehat{NOI}=\widehat{MOI}\)
Do đó: ΔONI=ΔOMI
Suy ra: IN=IM
Cho 2 góc xOy và mIn
Ox song song Im
Oy song song In
CM: 1.\(\widehat{xOy}=\widehat{mIn}\) (Nếu 2 góc cùng nhọn hay cùng tù)
2. \(\widehat{xOy}+\widehat{mIn}\)=180 độ( Nếu có một góc nhọn và một góc tù)
Giúp mình với mình sắp Kt rồi