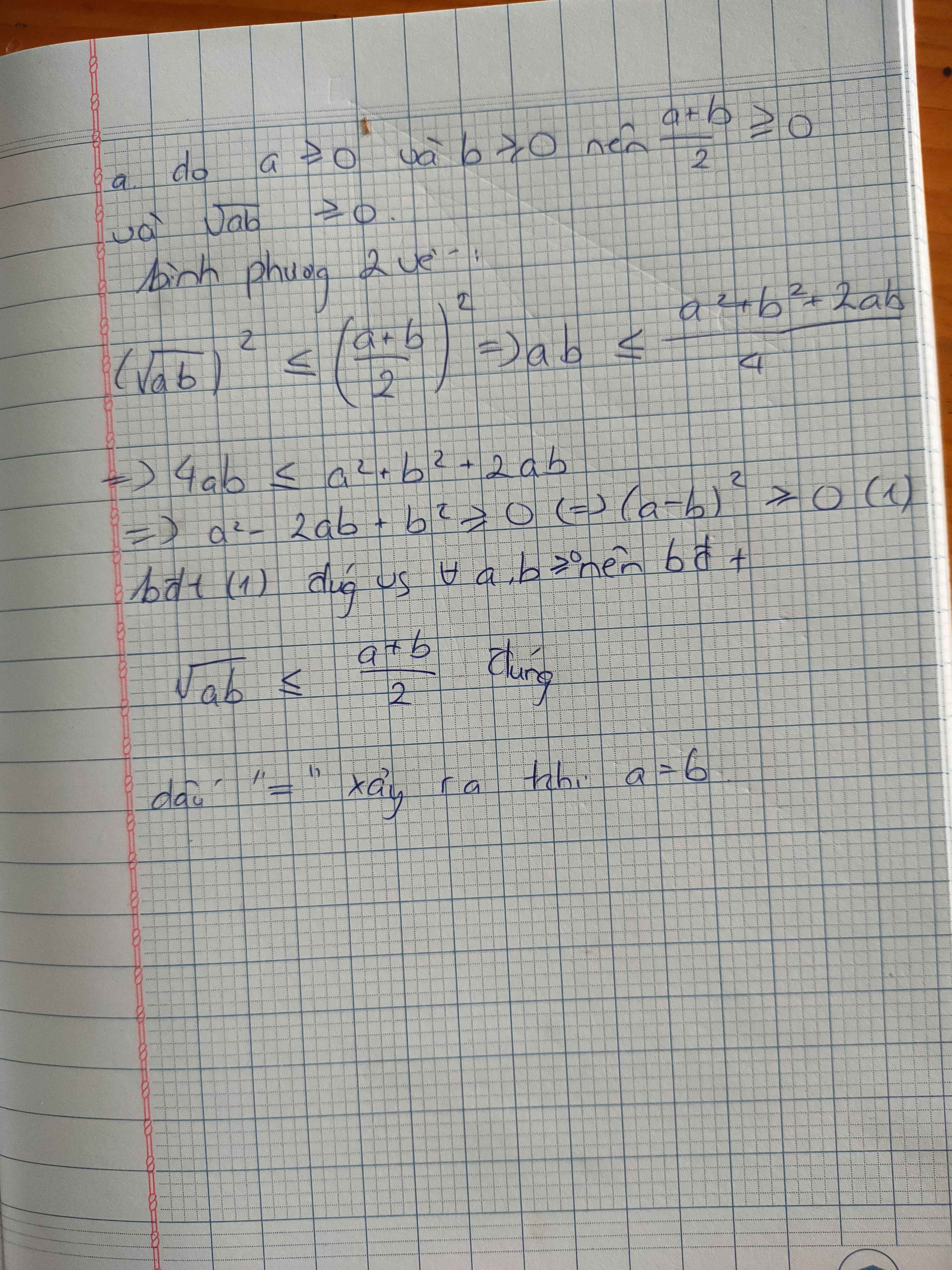chứng minh : 0:0=0

Những câu hỏi liên quan
chứng minh 0=1?????
không chứng minh theo kiểu 0 x 0 = 1 x 0
-20=-20
16-36=25-45
42-4.9=52-5.9
42-2.4.9292+814814=52-2.5.9292+814814
(4−92)2(4−92)2=(5−92)2(5−92)2
4-9292=5-9292
4=5
4-4=5-4
0=1
Đúng 0
Bình luận (0)
Luôn có: (a-b)2=(b-a)2
\(\Leftrightarrow\)a-b=b-a\(\Leftrightarrow\)2a=2b\(\Leftrightarrow\)a=b
Ta chọn: a=0 và b=1 \(\rightarrow\)0=1
Vậy 0=1
Đúng 0
Bình luận (0)
a) Cho m > 0 và m < 1. Chứng minh m 2 < m
b) Cho a > b > 0. Chứng minh a 2 − b 2 > 0 .
a) Ta có M < 1. Mà m > 0 nên m.m < m.1 hay m 2 < m.
b) Từ a > b > 0, ta suy ra được a 2 > ab > b 2 . Sử dụng tính chất bắc cầu và liên hệ giữa thứ tự với phép cộng ta có a 2 - b 2 > 0.
Đúng 0
Bình luận (0)
a) Cho m 2, chứng minh
m
2
−
2
m
0
.Cho a 0; b 0 và a b. Chứng minh
1
a
1
b
.Suy ra kết quả tương tự
a
≥
b
0
.
Đọc tiếp
a) Cho m > 2, chứng minh m 2 − 2 m > 0 .
Cho a < 0; b < 0 và a > b. Chứng minh 1 a < 1 b .
Suy ra kết quả tương tự a ≥ b > 0 .
a) Chú ý m > 2 thì m > 0.
b) Chú ý a < 0 và b < 0 thì ab > 0. Khi đó a > b, nhân hai vế với 1 ab > 0 ta thu được 1 b > 1 a . Tương tự a > 0, b > 0, a > b ta được 1 a < 1 b .
Đúng 0
Bình luận (0)
CHỨNG MINH RẰNG:
0+0=0
0+0=0 (ko có điều kiện phải chứng minh)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
a) Cho a ≥ 0, b ≥ 0. Chứng minh bất đẳng thức Cauchy: ![]()
b) Cho a, b, c > 0. Chứng minh rằng: ![]()
c) Cho a, b > 0 và 3a + 5b = 12. Tìm giá trị lớn nhất của tích P = ab
\(\left(\sqrt{a}-\sqrt{b}\right)^2\ge0\Leftrightarrow a+b-2\sqrt{ab}\ge0\Leftrightarrow a+b\ge2\sqrt{ab}\Leftrightarrow\frac{a+b}{2}\ge\sqrt{ab}\)
Đúng 2
Bình luận (0)
Chứng minh rằng:
a) \(\lim 0 = 0;\)
b) \(\lim \frac{1}{{\sqrt n }} = 0.\) \(\)
a) Vì \(\left| {{u_n}} \right| = \left| 0 \right| = 0 < 1\) nên theo định nghĩa dãy số có giới hạn 0 ta có \(\lim 0 = 0;\)
b) Vì \(0 < \left| {\frac{1}{{\sqrt n }}} \right| < 1\) nên theo định nghĩa dãy số có giới hạn 0 ta có \(\lim \frac{1}{{\sqrt n }} = 0.\)
Đúng 0
Bình luận (0)
Chứng minh
a/0,(123)+0,(876)=1
b/0,(123)×0,(630)=1
a) \(0,\left(123\right)+0,\left(876\right)=\frac{123}{999}+\frac{876}{999}=\frac{999}{999}=1\)
b) \(0,\left(123\right)\times0,\left(630\right)=\frac{123}{999}\times\frac{630}{999}\)
ko bằng 1 đc
Đúng 0
Bình luận (0)
Ta có: Một số thập phân vô hạn tuần hoàn có thể biểu diễn thành phân số. Cách biểu diễn như sau:
0,aaa...=\(\frac{a}{9}\) ; 0,abab...=\(\frac{ab}{99}\) ; 0,abcabc...=\(\frac{abc}{999}\) ; . . .
Với nhận xét như trên ta có:
0,(123) = 0,123123....= \(\frac{123}{999}\) =\(\frac{41}{333}\)
0,(876) = 0,876876.... = \(\frac{876}{999}\) =\(\frac{292}{333}\)
Vậy 0,(123) + 0,(876) = \(\frac{41}{333}+\frac{292}{333}=1\)
Câu b chứng minh tương tự.
Đúng 0
Bình luận (0)
cho a+b+c>0,abc>0,ab+bc+ac>0 chứng minh rằng a>0,b>0,c>0
+TH1: có 1 số < 0 là a, 2 số lớn hơn 0 là b,c
=> bc > 0 mà a < 0
=> abc < 0 (trái giả thiết) => không tồn tại trường hợp này.
+TH2: 2 số <0 là b,c ; 1 số lớn hơn 0 là a.
=> bc > 0; b+c < 0; a > 0
a+b+c > 0 => a > -(b+c) > 0 => a.(b+c) < -(b+c).(b+c) (nhân cả 2 vế với 1 số < 0 là (b+c) nên đổi chiều)
=> ab+bc+ca=a(b+c) + bc < -(b+c)2 + bc = -(b2+c2+bc) < 0 (do b2,c2,bc > 0) => trái giả thiết => không tồn tại trường hợp này.
+TH3: a,b,c < 0
=>abc < 0 => trái giả thiết => không tồn tại trường hợp này.
Vậy: a,b,c > 0
Đúng 0
Bình luận (0)
sao th2 k suy ra ab>0 và c<0 nên abc<0 luôn
Đúng 0
Bình luận (0)
chứng minh 0:0= 2
\(\frac{0}{0}=\frac{100-100}{100-100}=\frac{10^2-10^2}{100-100}=\frac{\left(10-10\right)\left(10+10\right)}{10\left(10-10\right)}=\frac{10+10}{10}=\frac{20}{10}=\frac{2}{1}=2\)
Đúng 0
Bình luận (0)
Vô lý nhé
Không có số nào chia hết cho 0
Đúng 0
Bình luận (0)
huy rio sai bước 5
10-10=0 nên o thể rút gọn cho 0 được
vd:2.0/100.0 = 0/0 chứ ko bằng 2/100
Đúng 0
Bình luận (0)
Xem thêm câu trả lời