Cho a ∈ Z ; b ∈ N* ; n ∈ N*. Chứng minh rằng:
a) Nếu a < b thì \(\dfrac{a}{b}< \dfrac{a+n}{b+n}\)
b) Nếu a > b thì \(\dfrac{a}{b}>\dfrac{a+n}{b+n}\)
c) Nếu a = b thì \(\dfrac{a}{b}=\dfrac{a+n}{b+n}\)
Những câu hỏi liên quan
Cho số phức z a+bi; a,bϵR; a0 thỏa mãn
z
-
1
+
z
-
2
a
b
Tính
z
1
+
z
-
A. ...
Đọc tiếp
Cho số phức z = a+bi; a,bϵR; a>0 thỏa mãn z - 1 + z - 2 = a = b Tính z 1 + z -
A. 3 2
B. 10
C. 5
D. 2
Cho số phức z = a+bi (a,b ∈ Z) thỏa mãn z+1+3i-|z|i = 0. Tính S = a +3b
A. S = 7/3
B. S = -5
C. S = 5
D. S = -7/3
Cho số phức z a + bi (a,b
∈
ℝ
) thỏa mãn z + 2i
z
¯
3 + 3i. Tính z. A. |z| 2 B. |z|
5
C. |z| 5 D. |z|
2
Đọc tiếp
Cho số phức z = a + bi (a,b ∈ ℝ ) thỏa mãn z + 2i z ¯ = 3 + 3i. Tính z.
A. |z| = 2
B. |z| = 5
C. |z| = 5
D. |z| = 2
Cho số phức za+bi thỏa mãn
z
-
1
z
-
i
và
z
-
3
i
z
+
i
. Giá trị của a + b bằng:
Đọc tiếp
Cho số phức z=a+bi thỏa mãn z - 1 = z - i và z - 3 i = z + i . Giá trị của a + b bằng:
Câu 1 : Cho số phức z thỏa mãn z + ( 2 - i )overline{z} 3 - 5i. Môđun của số phức w z - i bằng bao nhiêu ?Câu 2 : Cho số phức z a + bi, (a,b ∈ R ) thỏa mãn ( 3 + 2i )z + ( 2 - i )2 4 + i. Tính P a - b
Đọc tiếp
Câu 1 : Cho số phức \(z\) thỏa mãn \(z\) + ( 2 - i )\(\overline{z}\) = 3 - 5i. Môđun của số phức w = \(z \) - i bằng bao nhiêu ?
Câu 2 : Cho số phức \(z\) = a + bi, (a,b ∈ R ) thỏa mãn ( 3 + 2i )\(z\) + ( 2 - i )2 = 4 + i. Tính P = a - b
Cho số phức
z
a
+
b
i
a
,
b
∈
ℝ
thỏa
z
+
4
+
z
−
4
10
và
z
-
6
lớn nhất. T...
Đọc tiếp
Cho số phức z = a + b i a , b ∈ ℝ thỏa z + 4 + z − 4 = 10 và z - 6 lớn nhất. Tính S = a + b .
A. S = 5
B. S = -5
C. S = 11
D. S = -3
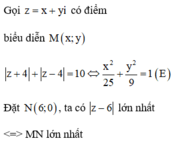
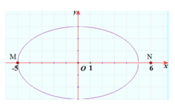
Vẽ trên hệ trục Oxy, nhận thấy MN lớn nhất khi M. Khi đó 
Chọn B
Đúng 0
Bình luận (0)
Cho hai số phức z a + bi và z’ a’ + b’i . Tìm điều kiện giữa a; b; a’; b’ để z + z’ là một số thuần ảo.
Đọc tiếp
Cho hai số phức z = a + bi và z’ = a’ + b’i . Tìm điều kiện giữa a; b; a’; b’ để z + z’ là một số thuần ảo.
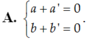
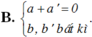
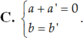
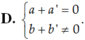
Chọn D.
Ta có: z + z’ = (a + a’) + (b + b’)i là số thuần ảo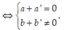 
Đúng 0
Bình luận (0)
31 tháng 10 2021 lúc 21:47
Cho 3 số a, b, c khác 0 và : a(y + z) = b(x + z) =c(z + y) Chứng minh rằng : y - z /a(b - c) = z - x / b(c - a) = x - y / c(a - b)
jup mik với a, cho a/b=c/d Chứng minh rằng (a^2+ac)/(c^2-ac)=(b^2+bd)/(d^2-bd)
b,cho 3 số x, y, z thỏa mãn y khác z và x+y khác z và z^2 = 2(xz + yz - xy) chứng minh rằng (x^2 + (x-z)^2)/(y^2+(y-z)^2)= x-z/y-z
ai nhanh mk tik cho
Cho số phức z = a + bi(a,b ∈ ℝ ) thỏa mãn z + 2 + i - |z|(1+i) = 0 và |z| > 1. Tính P = a + b
A. P = -1
B. P = -5
C. P = 3
D. P = 7
Đáp án D.
Đặt z = a + bi => a + bi 
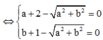
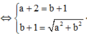
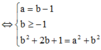
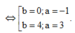
Do |z| > 1 => a = 3, b = 4
Đúng 0
Bình luận (0)