Chọn D.
Ta có: z + z’ = (a + a’) + (b + b’)i là số thuần ảo 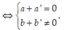
Chọn D.
Ta có: z + z’ = (a + a’) + (b + b’)i là số thuần ảo 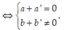
Cho hai số phức z = 1 + a i ( a ∈ R ) , z ' = 1 + i Tìm điều kiện của a để zz’ là một số thuần ảo
![]()
![]()
![]()
![]()
Cho hai số phức z = - 2 + 5 i , z ' = a + b i ( a , b ∈ R ) Xác định a,b để z + z’ là một số thuần ảo
![]()
![]()
![]()
![]()
Tìm số phức z thỏa mãn hai điều kiện:| z + 1 - 2i| = | z ¯ + 3 + 4i| và z - 2 i z ¯ + i là một số thuần ảo.
![]()
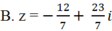
![]()
![]()
Cho số phức z = a + bi với a , b ∈ R . Nếu z là số thuần ảo thì đâu là khẳng định đúng?
A. a = 0
B. a = 0 và b ≠ 0
C. b = 0
D. b = 0 và a ≠ 0
Cho hai số phức z = a + b i , z ' = a ' + b ' i ( a , b , a ' , b ' ∈ ℝ )
Tìm phần ảo của số phức z z ' .
A. ( a b ' + a ' b ) i
B. a b ' + a ' b
C. a b ' - a ' b
D. a a ' - b b '
Cho hai số phức z = a + bi; a,b. Có điểm biểu diễn của số phức z nằm trong dải (-2;2) (hình 1) điều kiện của a và b là:
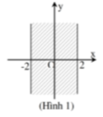
A. a ≥ 2 b ≥ 2
B. a ≤ - 2 b ≤ - 2
C. -2 < a < 2, b ∈ ℝ
D. a,b ∈ (-2;2)
Cho số phức z = ( a + b i ) 2 . Để là số thuần ảo thì
A. a = b = 1
B. a = b = -1
C. a = b = 0
D. |a| = |b|
Số phức z = a + bi(a, b thuộc R) là số thuần ảo khi và chỉ khi
A. a = 0; b ≠ 0
B. a ≠ 0; b = 0
C. a = 0
D. b = 0
Cho hai số phức z = a + b i và z ' = a ' + b ' i . Tìm phần ảo của số phức zz'
![]()
![]()
![]()
![]()