Chọn B.
Giả sử z = x + yi. Theo bài ra ta có: |x + 1 + (y – 2)i| = |x + 3 + (4 – y)i|
hay ( x + 1) 2+ ( y - 2) 2 = ( x + 3) 2 + ( y - 4) 2
suy ra y = x + 5
Số phức
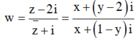
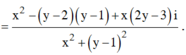
w là một số ảo
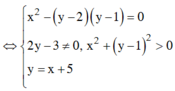
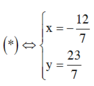
Vậy 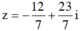
Chọn B.
Giả sử z = x + yi. Theo bài ra ta có: |x + 1 + (y – 2)i| = |x + 3 + (4 – y)i|
hay ( x + 1) 2+ ( y - 2) 2 = ( x + 3) 2 + ( y - 4) 2
suy ra y = x + 5
Số phức
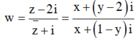
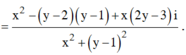
w là một số ảo
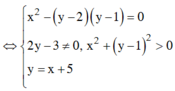
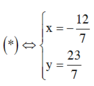
Vậy 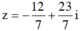
Có bao nhiêu số phức z thỏa mãn z + 1 - 2 i = z ¯ + 3 + 4 i và z - 2 i z + i ¯ là một số thuần ảo
![]()
![]()
![]()
![]()
Tìm nghịch đảo của số phức z, biết z thỏa mãn | z - 2i| =| z ¯ + 2 + 4i| và z - i z ¯ + i là số thuần ảo.
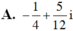
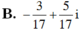

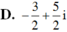
Cho số phức z thỏa mãn điều kiện ( 3 + 2 i ) z + ( 2 - i ) 2 = 4 + i . Tìm phần ảo của số phức w = ( 1 + z ) z ¯ .
![]()
![]()
![]()
![]()
Trong các số phức z thỏa mãn điều kiện z - 2 - 4 i = z - 2 i Số phức z có môđun nhỏ nhất có tổng phần thực và phần ảo là
A. 0.
B. 4.
C. 3.
D. 2.
Có bao nhiêu số phức z thỏa mãn các điều kiện z - 2 + i = 2 v à ( z + i ) 2 là số thuần ảo?
![]()
![]()
![]()
![]()
Cho z là các số phức thỏa mãn điều kiện z + 3 1 - 2 i + 2 = 1 và w là số thuần ảo.
Giá trị nhỏ nhất của biểu thức z - w bằng
A. 5 - 5
B. 5
C. 2 2
D. 1 + 3
Cho số phức z thỏa mãn điều kiện (z+2)(1+2i) = 5 z ¯ . Tìm phần ảo của số phức w = ( z + 2 i ) 2019
A . 2 1009
B . 0
C . - 2 1009
D . 2019
Trong các số phức thỏa mãn điều kiện z - 2 - 4 i = z - 2 i . Tìm môđun nhỏ nhất của số phức z+2i
A. 5
B. 3 5
C. 3 2
D. 3 + 2
Cho z là số phức thỏa mãn điều kiện 2 z − 1 1 + i + z ¯ + 1 1 − i = 2 − 2 i . Tính tổng bình phương phần thực và phần ảo của số phức w = 9 z 2 + 6 z + 1
A. 25
B. 1
C. 49
D. 41