
mỗi câu thôi mà
cân bằng
cân bằng mỗi câu thôi mà
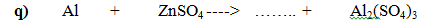
\(2Al+3ZnSO_4\rightarrow Al_2\left(SO_4\right)_3+3Zn\)
có mỗi câu thôi ạ
cân bằng
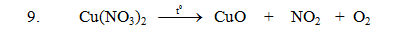
\(2Cu\left(NO_3\right)_2\xrightarrow[]{t^0}2CuO+4NO_2+O_2\)
có mỗi câu thôi ạ
cân bằng
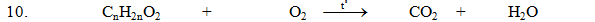
\(C_nH_{2n}O_2+\dfrac{3n-2}{2}O_2\) \(\underrightarrow{to}\) \(nCO_2+nH_2O\)
có mỗi câu thôi ạ
cân bằng
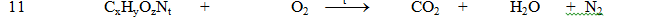
\(C_xH_yO_zN_t+\left(x+\dfrac{y}{4}-\dfrac{z}{2}\right)O_2\xrightarrow[]{t^o}xCO_2+\dfrac{y}{2}H_2O+\dfrac{t}{2}N_2\)
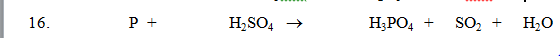
cân bằng
có mỗi câu thôi ạ
\(2P+5H_2SO_{4_{đặc}}\xrightarrow[]{t^o}2H_3PO_4+5SO_2+2H_2O\)
có mỗi 1 câu thôi ạ
cân bằng
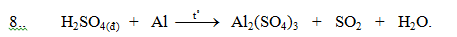
\(6H_2SO_{4\left(đ\right)}+2Al\xrightarrow[]{t^0}Al_2\left(SO_4\right)_3+3SO_2+6H_2O\)
mỗi câu 4 thôi

Bài 4:
b: Xét ΔAHB vuông tại H có HE là đường cao ứng với cạnh huyền AB
nên \(AE\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HF là đường cao ứng với cạnh huyền AC
nên \(AF\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AE\cdot AB=AF\cdot AC\)
Câu đầu ấy ạ-em hỏi mỗi câu ấy thôi ^_^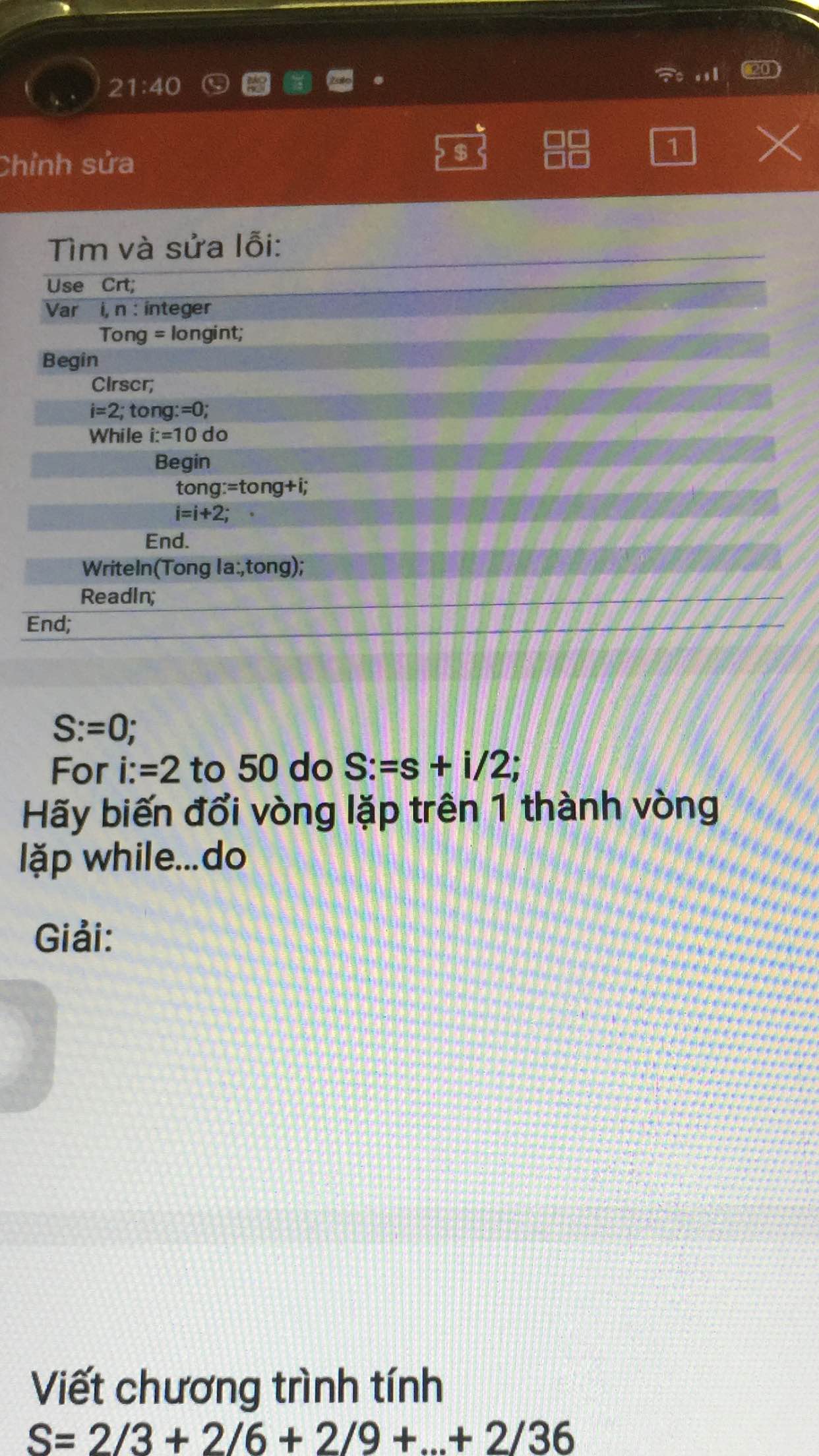
Ở dòng thứ 2 bạn thiếu dấu ; sửa lại: Thêm ; ở cuối dòng 2
ở dòng thứ 3 bạn sai dấu =; sửa lại: Thay dấu = thành dấu :
Ở dòng thứ 6 bạn sai chỗ i=; sửa lại: i:=
Ở dòng thứ 7 bạn sai chỗ i:=10; sửa lại: i<=10;
Ở dòng thứ 10 bạn sai chỗ i=i+2; sửa lại: i:=i+2;
Ở dòng thứ 11 bạn sai chỗ dấu end. Sửa lại: end;
Ở dòng thứ 12 bạn sai chỗ trong dấu (): Sửa lại: ('Tong la: ',tong);
Ở dòng cuối bạn sai chỗ dấu ; Sửa lại: end.
Mỗi câu 1 thôi ạ
Câu 1:
a: \(2\sqrt{18}-\dfrac{1}{5}\sqrt{50}+3\sqrt{98}-\sqrt{288}\)
\(=6\sqrt{2}-\sqrt{2}+21\sqrt{2}-12\sqrt{2}\)
\(=14\sqrt{2}\)
b: \(\sqrt{\left(1-\sqrt{3}\right)^2}+\sqrt{7-4\sqrt{3}}\)
\(=\sqrt{3}-1+2-\sqrt{3}\)
=1