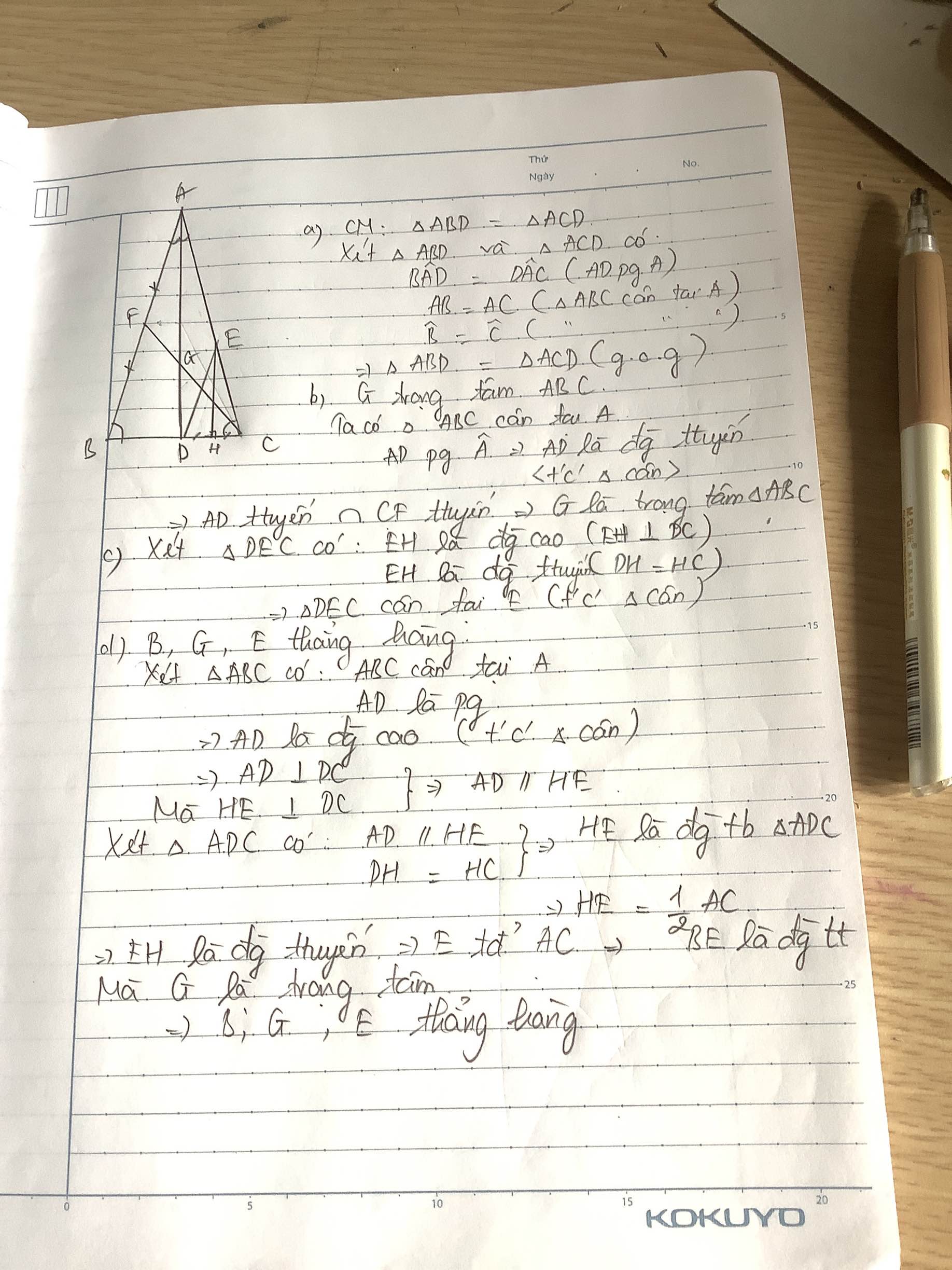Cho tam giác ABC cân tại A,AD là đường cao,H là trực tâm ,biết góc BAC<90o,AH=14,BH=HC=30.Tính AD

Những câu hỏi liên quan
Cho tam giác ABC cân tại A , đường cao AD , trực tâm H, biết rằng góc BAC <90 độ . AH=14cm; BH=HC =30cm. Tính AD=?
CHo tam giác ABC có 3 góc nhọn nội tiếp đường tròn (O; R) và H là trực tâm của tam giác ABC. Đường cao AD cắt đường tròn tại điểm M khác A. Vẽ đường kính AN. a) CM: BH // CN
b) CM: DH = DM
c) Biết AH = R. Tính góc BAC
(Giải câu c thôi)
Cho tam giac ABC có góc A nhọn , H là trực tâm , đường cao BK . Biết AH=BC.
a, Chứng minh tam giác AKH= tam giác BKC
b,Tính góc BAC
a: Xét ΔAKH vuông tại K và ΔBKC vuông tại K có
AH=BC
\(\widehat{KAH}=\widehat{KBC}\left(=90^0-\widehat{C}\right)\)
Do đó: ΔAKH=ΔBKC
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A, có góc BAC nhọn. Qua A vẽ tia phân giác của góc BAC cắt cạnh BC tại D.a) Chứng minh ΔABD ΔACD.b) Vẽ đường trung tuyến CF của tam giác ABC cắt cạnh AD tại G. Chứng minh G là trọng tâm của tam giác ABC.c) Gọi H là trung điểm của cạnh DC. Qua H vẽ đường thẳng vuông góc với cạnh DC cắt cạnh AC tại E. Chứng minh ΔDEC cân.Chứng minh ba điểm B, G, E thẳng hàng và AD BD
Đọc tiếp
Cho tam giác ABC cân tại A, có góc BAC nhọn. Qua A vẽ tia phân giác của góc BAC cắt cạnh BC tại D.
a) Chứng minh ΔABD = ΔACD.
b) Vẽ đường trung tuyến CF của tam giác ABC cắt cạnh AD tại G. Chứng minh G là trọng tâm của tam giác ABC.
c) Gọi H là trung điểm của cạnh DC. Qua H vẽ đường thẳng vuông góc với cạnh DC cắt cạnh AC tại E. Chứng minh ΔDEC cân.
Chứng minh ba điểm B, G, E thẳng hàng và AD > BD
a) Xét ΔABD và ΔACD có
AB=AC(ΔBAC cân tại A)
\(\widehat{BAD}=\widehat{CAD}\)(AD là tia phân giác của \(\widehat{BAC}\))
AD chung
Do đó: ΔABD=ΔACD(c-g-c)
Đúng 1
Bình luận (0)
b) Ta có: ΔABD=ΔACD(cmt)
nên DB=DC(hai cạnh tương ứng)
mà B,D,C thẳng hàng(gt)
nên D là trung điểm của BC
Xét ΔABC có
AD là đường trung tuyến ứng với cạnh BC(cmt)
CF là đường trung tuyến ứng với cạnh AB(gt)
AD cắt CF tại G(gt)
Do đó: G là trọng tâm của ΔABC(Tính chất ba đường trung tuyến của tam giác)
Đúng 0
Bình luận (0)
c) Xét ΔADC có
H là trung điểm của DC
HE//AD(cùng vuông góc với DC)
Do đó: E là trung điểm của AC(Định lí 1 đường trung bình của tam giác)
Ta có: ΔADC vuông tại D(gt)
mà DE là đường trung tuyến ứng với cạnh AC(cmt)
nên DE=CE
hay ΔDEC cân tại E
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A, có góc BAC nhọn. Qua A vẽ tia phân giác của góc BAC cắt cạnh BC tại D.a) Chứng minh ΔABD ΔACD.b) Vẽ đường trung tuyến CF của tam giác ABC cắt cạnh AD tại G. Chứng minh G là trọng tâm của tam giác ABC.c) Gọi H là trung điểm của cạnh DC. Qua H vẽ đường thẳng vuông góc với cạnh DC cắt cạnh AC tại E. Chứng minh ΔDEC cân.Chứng minh ba điểm B, G, E thẳng hàng
Đọc tiếp
Cho tam giác ABC cân tại A, có góc BAC nhọn. Qua A vẽ tia phân giác của góc BAC cắt cạnh BC tại D.
a) Chứng minh ΔABD = ΔACD.
b) Vẽ đường trung tuyến CF của tam giác ABC cắt cạnh AD tại G. Chứng minh G là trọng tâm của tam giác ABC.
c) Gọi H là trung điểm của cạnh DC. Qua H vẽ đường thẳng vuông góc với cạnh DC cắt cạnh AC tại E. Chứng minh ΔDEC cân.
Chứng minh ba điểm B, G, E thẳng hàng
Mình đang cần gấp giúp mình với ạ .Cảm ơn ạ
Đúng 1
Bình luận (1)
a: Xét ΔABD và ΔACD có
AB=AC
\(\widehat{BAD}=\widehat{CAD}\)
AD chung
Do đó: ΔABD=ΔACD
b: Ta có: ΔABD=ΔACD
nên BD=CD
hay D là trung điểm của BC
Xét ΔABC có
AD là đường trung tuyến ứng với cạnh BC
CF là đường trung tuyến ứng với cạnh AB
AD cắt CF tại G
DO đó: G là trọng tâm của ΔBAC
Xét ΔABC có
H là trung điểm của DC
HE//AD
Do đó: E là trung điểm của AC
Ta có: ΔADC vuông tại D
mà DE là đường trung tuyến ứng với cạnh huyền AC
nên DE=CE=AE
Xét ΔDEC có ED=EC
nên ΔDEC cân tại E
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC cân tại A, có góc BAC nhọn. Qua A vẽ tia phân giác của góc BAC cắt cạnh BC tại D.a) Chứng minh ΔABD ΔACD.b) Vẽ đường trung tuyến CF của tam giác ABC cắt cạnh AD tại G. Chứng minh G là trọng tâm của tam giác ABC.c) Gọi H là trung điểm của cạnh DC. Qua H vẽ đường thẳng vuông góc với cạnh DC cắt cạnh AC tại E. Chứng minh ΔDEC cân.d) Chứng minh ba điểm B, G, E thẳng hàng và AD BD.Cả hình nữa nhé, làm nhanh giúp mình với mai nộp rồi:
Đọc tiếp
Cho tam giác ABC cân tại A, có góc BAC nhọn. Qua A vẽ tia phân giác của góc BAC cắt cạnh BC tại D.
a) Chứng minh ΔABD = ΔACD.
b) Vẽ đường trung tuyến CF của tam giác ABC cắt cạnh AD tại G. Chứng minh G là trọng tâm của tam giác ABC.
c) Gọi H là trung điểm của cạnh DC. Qua H vẽ đường thẳng vuông góc với cạnh DC cắt cạnh AC tại E. Chứng minh ΔDEC cân.
d) Chứng minh ba điểm B, G, E thẳng hàng và AD > BD.
Cả hình nữa nhé, làm nhanh giúp mình với mai nộp rồi:<<
a: XétΔABD và ΔACD có
AB=AC
\(\widehat{BAD}=\widehat{CAD}\)
AD chung
DO đó: ΔABD=ΔACD
b: XétΔABC có
AD là đường trung tuyến
CF là đường trung tuyến
AD cắt CF tại G
Do đó: G là trọng tâm của ΔABC
Đúng 1
Bình luận (0)
Cho tam giác ABC cân tại A (A<900 ). Đường cao BD , trên tia BD lấy K sao cho BK=AB . Gọi H là trực tâm tam giác ABC
a, Tính góc HAK
b, Tính góc BAC biết CH=2cm
Mấy bn giúp mk vs mk đang cần gấp
cho tam giác ABC cân tại A. Đường cao AG, BE,CF cắt nhau tại H. I là tâm đường tròn ngoai tiếp tứ giác AEHF . cho (I,r) và góc BAC là anpha. độ dài BE của tam giác ABC
cho tam giác abc cân tại a. Kẻ đường cao BE. Trên cạnh AB lấy D sao cho AD=AE. Gọi H là giao điểm của BE và CD. Cm H là trực tâm tam giác ABC
Xét tg ABE va tg ACD, co
+/Goc A chung
+/AB=AC [vi tg ABC can]
+/AD=AE[GT]
Vay tgABE=tgACD [c.g.c]
Suy ra góc AEB=góc ADC[vì là hai cạnh tương ứng]
Mà góc AEB=90[độ theo gt]
suy ra góc ADC=90[độ vì cũng bằng với góc AEB]
Hãy cạnh ĐC là đường cao
2 đường cao ĐC và BÈ cùng đi qua điểm H
Vậy H chính là đường trung trực của tg cân ABC
[NẾU BÀI CỦA MÌNH ĐÚNG HAY TÍCH ĐỂ NHÉ]
Đúng 0
Bình luận (0)