Cho tam giác ABC tia phân giác của góc B cắt AC tại D Gọi N là giao điểm của hai đường thẳng AB và BC. So sánhDE và D F

Những câu hỏi liên quan
cho tam giác ABC vuông tại A(AB<AC), tia phân giác góp ABC cắt AC tại D . vẽ DE vuông góc với BC tại E. Gọi F là giao điểm của đường thẳng AB và DE
a, Chứng minh tam giác ABD= tam giác EBD và tam giác CDF là tam giác cân
b, So sánh DE và DF
Mình cần câu b, thôi
a: XétΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó:ΔBAD=ΔBED
Xét ΔADF vuông tại A và ΔEDC vuông tại E có
DA=DE
\(\widehat{ADF}=\widehat{EDC}\)
Do đó: ΔADF=ΔEDC
Suy ra: DF=DC
hay ΔDFC cân tại D
b: Ta có: DE=DA
mà DA<DF
nên DE<DF
Đúng 1
Bình luận (0)
cho tam giác abc vg tại a.Trên cạnh bc lấy điểm d sao cho bdab.Qua d vẽ đường thẳng vg góc với bc cắt tia đối của tia ab tại e.a, C/m tam giác abc tam giác dbe.b,Gọi h là giao điểm của ed và ac.c/m:bh là tia phân giác của abc.c,cho db 6cm,dc 4cm.Tính ab,ac.d,Qua b vẽ đường thẳng vuông góc với ab cắt đường thẳng ed tại k.c/m tam giác kbh là tam giác cân.e,Gọi f là trung điểm của ec.c/m ba điểm b,h,f thẳng hàng
Đọc tiếp
cho tam giác abc vg tại a.Trên cạnh bc lấy điểm d sao cho bd=ab.Qua d vẽ đường thẳng vg góc với bc cắt tia đối của tia ab tại e.
a, C/m tam giác abc= tam giác dbe.
b,Gọi h là giao điểm của ed và ac.c/m:bh là tia phân giác của abc.
c,cho db = 6cm,dc= 4cm.Tính ab,ac.
d,Qua b vẽ đường thẳng vuông góc với ab cắt đường thẳng ed tại k.c/m tam giác kbh là tam giác cân.
e,Gọi f là trung điểm của ec.c/m ba điểm b,h,f thẳng hàng
a, xét tam giác ABC và tam giác DBE có : góc B chung
AB = BD (Gt)
góc BAC = góc BDE = 90
=> tam giác ABC = tam giác DBE (cgv-gnk)
b, xét tam giác ABH và tam giác DBH có : BH chung
AB = BD (Gt)
góc HAB = góc HDB = 90
=> tam giác ABH = tam giác DBH (ch-cgv)
=> góc ABH = góc DBH (đn) mà BH nằm giữa AB và BD
=> BH là pg của góc ABC (đn)
c, AB = BD (gt) có BD = 6 (gt)
=> AB = 6
BD + DC = BC
BD = 6; CD = 4
=> BC =10
tam giác ABC vuông tại A (Gt)
=> BC^2 = AB^2 + AC^2
=> AC^2 = 10^2 - 6^2
=> AC^2 = 64
=> AC = 8 do AC > 0
Cho tam giác ABC vuông tại A, tia phân giác trong của góc B cắt AC tại D
a. Cho BC = 10cm, AB = 6cm, AD = 3cm.Tính AC và CD
b. Vẽ DE vuông góc với BC tại E. CMR: tam giác ABD = tam giác EBD, và tam giác BAE cân
c Gọi F là giao điểm của hai đường thẳng AB và DE. So sánh DE và DF
A) XÉT \(\Delta ABC\)VUÔNG TẠI A
\(\Rightarrow BC^2=AB^2+AC^2\left(PYTAGO\right)\)
THAY \(10^2=6^2+AC^2\)
\(100=36+AC^2\)
\(\Rightarrow AC^2=100-36\)
\(\Rightarrow AC^2=64\)
\(\Rightarrow AC=\sqrt{64}=8\left(cm\right)\)
ta có \(AD+DC=AC\)
\(\Leftrightarrow3+DC=8\)
\(\Leftrightarrow DC=8-3=5\left(cm\right)\)
B) XÉT \(\Delta ABD\)VÀ \(\Delta EBD\)CÓ
\(\widehat{BAD}=\widehat{BED}=90^o\)
\(\widehat{ABD}=\widehat{EBD}\left(gt\right)\)
BD LÀ CẠNH CHUNG
=>\(\Delta ABD\)=\(\Delta EBD\)( CH-GN)
\(\Rightarrow BA=BE\)(HAI CẠNH TƯƠNG ỨNG )
=> \(\Delta BAE\)LÀ TAM GIÁC CÂN TẠI B
c) XÉT \(\Delta ADF\)VUÔNG TẠI A
\(\Rightarrow DF>AD\left(1\right)\)( CẠNH HUYỀN LỚN NHẤT )
VÌ \(\Delta ABD\)=\(\Delta EBD\)(CMT)
=> \(AD=ED\left(2\right)\)(HAI CẠNH TƯƠNG ỨNG )
TỪ (1) VÀ (2)
\(\Rightarrow DF>ED\)
Cho tam giác ABC vuông tại A , tia phân giác của góc ABC cắt AC tại D . Vẽ DE vuông góc BC tại E . Gọi F là giao của AB và DE . Gọi H là giao điểm của hai đường thẳng BD và CF . Trên tia đối của tia DF lấy điểm K sao cho DK = DF . Gọi I là giao điểm của KH và CD :
a) So sánh DE và DF
b ) Chứng minh CI = 2DI
cho tam giác ABC tia phân giác của góc B và góc C cắt nhau tại I .Qua I kẻ đường thẳng // với BC .Gọi giao điểm của đường thẳng này với AB,AC thứ tự là D,E .Tính E,F
cho tam giác ABC vuông tại A .(AB<AC).tia phân giác của góc ABC cắt AC tại D, DN vuông góc với BC tại N
a) chứng minh tam giác ABD = tam giác NBD.
b)gọi K là giao điểm của hai đường thẳng BA và ND . chứng minh tam giác AKC cân .vẽ EH vuông góc với BC tại H . chứng minh BC+ AH>EK+AB
cho tam giác ABC vuông tại A .(AB<AC).tia phân giác của góc ABC cắt AC tại D, DN vuông góc với BC tại N
a) chứng minh tam giác ABD = tam giác NBD.
b)gọi K là giao điểm của hai đường thẳng BA và ND . chứng minh tam giác AKC cân .vẽ EH vuông góc với BC tại H . chứng minh BC+ AH>EK+AB
cho tam giác abc vuông tại a và góc abc= 60 độ
a) so sánh ab và ac
b) trên cạnh bc lấy điểm d sao cho bd=ab. qua d dựng đường thẳng vuông góc với bc cắt tia đối ab tại e. chứng minh tam giác abc= tam giác dbe
c) gọi h là giao điểm của ed và a. chứng minh tia bh là tia phân giác của góc abc
d) qua b dựng đường vuông góc với ab cắt đường thẳng ed tại k. chứng minh tam giác hbk đều
tam giác ABC vuông tại A (gt)
=> góc B + góc C = 90
mà góc B = 60
=> góc C = 30
=> góc C < góc B xét tam giác ABC
=> AB < AC (đl)
Đúng 2
Bình luận (0)
tgiac ABC vuông ở , B=60¤=> C=30¤
=>AC>AB vì
AC là cạnh đối diện với góc lớn hơn (60¤)
AB.......................................nhở hơn (30¤)..
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A. Tia phân giác góc B cắt cạnh AC tại điểm M. Kẻ
M
D
⊥
B
C
(
D
∈
B
C
)
.
a) Chứng minh BA BD.b) Gọi E là giao điểm của hai đường thẳng DM và BA. Chứng minh
∆
A
B
C
∆
D
B
E
.
c) Kẻ
D
H
⊥
M
C
(
H
∈
M
C...
Đọc tiếp
Cho tam giác ABC vuông tại A. Tia phân giác góc B cắt cạnh AC tại điểm M. Kẻ M D ⊥ B C ( D ∈ B C ) .
a) Chứng minh BA = BD.
b) Gọi E là giao điểm của hai đường thẳng DM và BA. Chứng minh ∆ A B C = ∆ D B E .
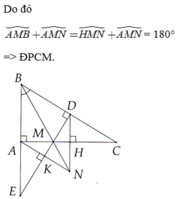
c) Kẻ D H ⊥ M C ( H ∈ M C ) và A K ⊥ M E ( K ∈ M E ) . Gọi N là giao điểm của hai tia DH và AK. Chứng minh MN là tia phân giác góc HMK.
d) Chứng minh ba điểm B, M, N thẳng hàng.
Cho tam giác ABC vuông tại A, tia phân giác của góc ABC cắt AC tại D.a) Cho biết BC10cm, AB6cm, AD3cm. Tính AC, CDb)Vẽ DE vuông góc với BC tại F. CM: tam giác ABD tam giác EBD và tam giác BAE cânc) Gọi F là giao điểm của AB và DE. So sánh DE và DFd)Gọi H là giao điểm của BD và CF. K là điểm trên tia đối của tia DF sao cho DK DF. I là điểm trên đoạn thẳng CD sao cho CI 2DI. CM:K, H, I thẳng hàng
Đọc tiếp
Cho tam giác ABC vuông tại A, tia phân giác của góc ABC cắt AC tại D.
a) Cho biết BC=10cm, AB=6cm, AD=3cm. Tính AC, CD
b)Vẽ DE vuông góc với BC tại F. CM: tam giác ABD= tam giác EBD và tam giác BAE cân
c) Gọi F là giao điểm của AB và DE. So sánh DE và DF
d)Gọi H là giao điểm của BD và CF. K là điểm trên tia đối của tia DF sao cho DK = DF. I là điểm trên đoạn thẳng CD sao cho CI = 2DI. CM:K, H, I thẳng hàng