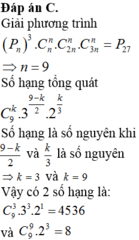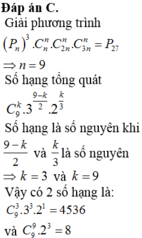Cho n là số dương.Chứng minh: T= 23n+1−23n−1+1 là hợp số

Những câu hỏi liên quan
Cho A=n^6-n^4+2n^3+23n^2( với n thuộc N, n>1)\chứng minh rằng A không phải là số chính phương
Chứng minh với mọi số tự nhiên n thì 11.52n+33n+2+23n+1 chia hết cho 17.
\(11.5^{2n}+3^{3n+2}+2^{3n+1}\)\(=11.25^n+8^n.4+8^n.2\)\(=11.25^n+6.8^n\)
Vì 25 = 8 (dư 17)
➩ \(11.5^{2n}+3^{3n+2}+2^{3n+1}\)\(=11.25^n+6.8^n\)\(=11.8^n+6.8^n=17.8^n=0\) (dư 17)
Hay \(11.5^{2n}+3^{3n+2}+2^{3n+1}\) ⋮ 17
Đúng 3
Bình luận (0)
tìm số tự nhiên n nhỏ nhất để số 2^2023+23n là 1 bội số của 31
Đặt \(A=2^{2023}+23n=8.2^{2020}+23n=8.\left(2^5\right)^{404}+23n=8.32^{404}+23n\)
Do \(32\equiv1\left(mod31\right)\Rightarrow32^{404}\equiv1\left(mod31\right)\)
\(\Rightarrow8.32^{404}\equiv8\left(mod31\right)\)
\(\Rightarrow A\) chia hết cho 31 khi và chỉ khi \(23n+8\) chia hết 31
\(\Rightarrow n=1\) là giá trị nhỏ nhất thỏa mãn
Đúng 1
Bình luận (0)
ai giúp m vs m sẽ like
Cho A=n^6-n^4+2n^3+23n^2( với n thuộc N, n>1)\chứng minh rằng A không phải là số chính phương
Tìm ba chữ số tận cùng của:
a) 23n.47n (n\(\in\)N*) b) 23n+3.47n+2 (n\(\in\)N)
Cho \(\dfrac{23n^2-1}{35}\in Z\)
Chứng minh các phân số sau tối giản\(\dfrac{n}{5}\);\(\dfrac{n}{7}\)
Ta có: \(\dfrac{23n^2-1}{35}\in Z\)
\(\Rightarrow23n^2-1=35k\left(k\in Z\right)\)
\(\Rightarrow23n^2=35k+1\)
Mà 35k + 1 chia cho 5 hoặc 7 đều dư 1 nên 23n2 chia cho 5 hoặc 7 đều dư 1
Hay n không chia hết cho 5, 7
Vậy \(\dfrac{n}{5},\dfrac{n}{7}\) là các phân số tối giản
Đúng 0
Bình luận (0)
Tìm các số hạng (nhỏ hơn 100) là số nguyên trong khai triển nhị thức
3
+
2
3
n
biết
P
n
3
.
C
n
n
.
C
3
n...
Đọc tiếp
Tìm các số hạng (nhỏ hơn 100) là số nguyên trong khai triển nhị thức 3 + 2 3 n biết P n 3 . C n n . C 3 n n . C 3 n n = P 27 với n là số tự nhiên
A. 4536
B. 2196
C. 8
D. 10
Tìm các số hạng (nhỏ hơn 100) là số nguyên trong khai triển nhị thức
3
+
2
3
n
biết
P
n
3
.
C
n
n
.
C
3
n
n
.
C
3
n...
Đọc tiếp
Tìm các số hạng (nhỏ hơn 100) là số nguyên trong khai triển nhị thức 3 + 2 3 n biết P n 3 . C n n . C 3 n n . C 3 n n = P 27 với n là số tự nhiên
A. 4536
B. 2196
C. 8
D. 10
Tìm hệ số chứa
x
10
trong khai triển
f
x
1
4
x
2
+
x
+
1
2...
Đọc tiếp
Tìm hệ số chứa x 10 trong khai triển f x = 1 4 x 2 + x + 1 2 x + 2 3 n với n là số tự nhiên thỏa mãn hệ thức A n 3 + C n n - 2 = 14 n
![]()
![]()
![]()
![]()