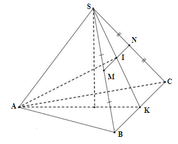
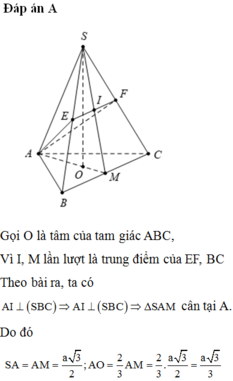
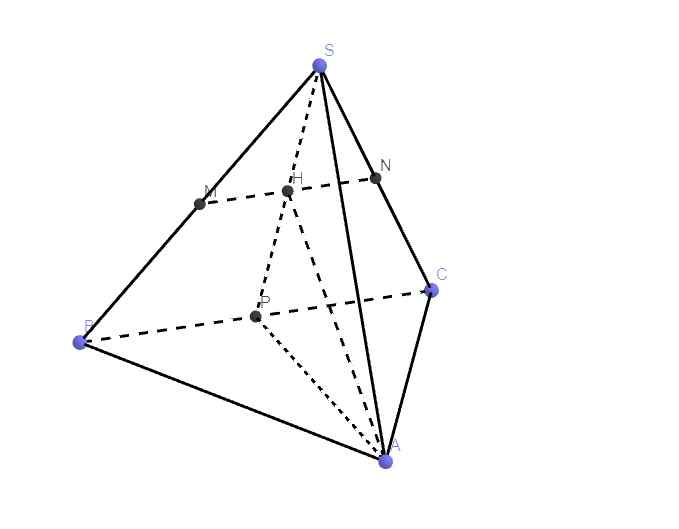
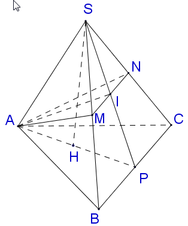
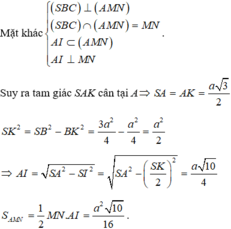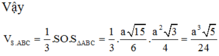Cho chóp tam giác đều S.ABC đỉnh S, có độ dài đáy bằng a, cạnh bên bằng a\(\sqrt{3}\) /2 . Gọi M là trung điểm của SB.Mặt phẳng α chứa AM vuông góc với mặt SBC, cắt SC tại N.Tính theo a diện tích tam giác AMN

Những câu hỏi liên quan
Cho hình chóp tam giác đều S.ABC đỉnh S, có độ dài cạnh đáy bằng a. Gọi M và N lần lượt là trung điểm của các cạnh SB và SC. Biết mặt phẳng ( AMN ) vuông góc với mặt phẳng ( SBC ). Tính diện tích tam giác AMN theo a.
Cho hình chóp tam giác đều S.ABC đỉnh S, có độ dài cạnh đáy bằng a. Gọi M, N lần lượt là trung điểm các cạnh SB và SC. Tính theo a diện tích tam giác AMN biết rằng mặt phẳng (AMN) vuông góc với mặt phẳng (SBC). A.
a
2
7
9
B.
a
2
10...
Đọc tiếp
Cho hình chóp tam giác đều S.ABC đỉnh S, có độ dài cạnh đáy bằng a. Gọi M, N lần lượt là trung điểm các cạnh SB và SC. Tính theo a diện tích tam giác AMN biết rằng mặt phẳng (AMN) vuông góc với mặt phẳng (SBC).
A. a 2 7 9
B. a 2 10 16
C. a 2 10 8
D. a 2 5 8
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AB=a, SA vuông góc với mặt phẳng (ABC), góc giữa 2 mặt phẳng (SBC) và (ABC) bằng 30 độ. Gọi M là trung điểm của cạnh SC. Tính thể tích khối chóp S.ABM theo a.
Ta có : \(SA\perp BC\), \(AB\perp BC\) \(\Rightarrow SB\perp BC\)
Do đó : góc giữa 2 mặt phẳng (SBC) và (ABC) bằng \(\widehat{SBA}=30^0\)
\(V_{S.ABM}=\frac{1}{2}V_{S.ABC}=\frac{1}{2}SA.AB.BC\)
\(BC=AB=a;SA=AB.\tan30^0=\frac{a\sqrt{3}}{3}\)
Vậy \(V_{s.ABM}=\frac{a^3\sqrt{3}}{36}\)
Đúng 0
Bình luận (0)
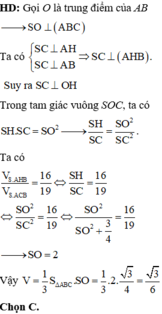
Cho hình chóp đều S.ABC có đáy là tam giác đều cạnh a. Gọi E, F lần lượt là trung điểm của các cạnh SB, SC. Biết mặt phẳng (AEF) vuông góc với mặt phẳng (SBC). Thể tích khối chóp S.ABC bằng A.
a
3
5
24
B.
a
3
5...
Đọc tiếp
Cho hình chóp đều S.ABC có đáy là tam giác đều cạnh a. Gọi E, F lần lượt là trung điểm của các cạnh SB, SC. Biết mặt phẳng (AEF) vuông góc với mặt phẳng (SBC). Thể tích khối chóp S.ABC bằng
A. a 3 5 24
B. a 3 5 8
C. a 3 4 24
D. a 3 6 12
Đáp án A
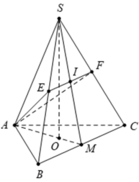
Gọi O là tâm của tam giác ABC, Vì I, M lần lượt là trung điểm của EF, BC
Theo bài ra, ta có ![]() cân tại A
cân tại A
Do đó 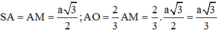
![]()
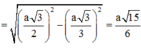
Vậy 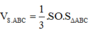
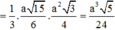
Đúng 0
Bình luận (0)
Cho hình chóp đều S.ABC có đáy là tam giác đều cạnh a. Gọi E, F lần lượt là trung điểm của các cạnh SB, SC. Biết mặt phẳng (AEF) vuông góc với mặt phẳng (SBC). Thể tích khối chóp S.ABC bằng
Đọc tiếp
Cho hình chóp đều S.ABC có đáy là tam giác đều cạnh a. Gọi E, F lần lượt là trung điểm của các cạnh SB, SC. Biết mặt phẳng (AEF) vuông góc với mặt phẳng (SBC). Thể tích khối chóp S.ABC bằng
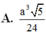
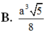
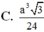
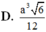
Cho hình chóp đều S.ABC, có đáy là tam giác đều cạnh bằng a. gọi M, N lần lượt là trung điểm của các cạnh SB, SC. Biết mặt phẳng (AMN) vuông góc với mặt phẳng (SBC). Tính thể tích của khối chóp A.BCNM.
Gọi H là trung điểm MN \(\Rightarrow SH\perp MN\)
Do chóp SABC đều \(\Rightarrow\Delta AMN\) cân tại A \(\Rightarrow AH\perp MN\Rightarrow AH\perp\left(SBC\right)\)
\(\Rightarrow AH\perp SH\)
Nối SH kéo dài cắt BC tại P \(\Rightarrow\) P là trung điểm BC đồng thời H là trung điểm SP (Talet)
\(\Rightarrow\) AH là đường cao đồng thời là trung tuyến trong tam giác SAP
\(\Rightarrow\Delta SAP\) cân tại A
\(\Rightarrow SA=AP=\dfrac{a\sqrt{3}}{2}\)
\(SH=\dfrac{1}{2}\sqrt{SB^2-BP^2}=\dfrac{1}{2}\sqrt{SA^2-\left(\dfrac{a}{2}\right)^2}=\dfrac{a\sqrt{2}}{4}\)
\(MN=\dfrac{1}{2}BC=\dfrac{a}{2}\) ; \(HP=SH=\dfrac{a\sqrt{2}}{4}\)
\(AH=\sqrt{SA^2-SH^2}=\dfrac{a\sqrt{10}}{4}\)
\(V=\dfrac{1}{3}AH.\dfrac{1}{2}\left(MN+BC\right).HP=...\)
Đúng 0
Bình luận (0)
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a. Gọi M,N lần lượt là trung điểm của SB,SC. Tính thể tích khối chóp ABCMN. Biết mặt phẳng (AMN) vuông góc với mặt phẳng (SBC). A.
2
a
3
16
B.
2
a
3
8...
Đọc tiếp
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a. Gọi M,N lần lượt là trung điểm của SB,SC. Tính thể tích khối chóp ABCMN. Biết mặt phẳng (AMN) vuông góc với mặt phẳng (SBC).
A. 2 a 3 16
B. 2 a 3 8
C. 3 2 a 3 16
D. 2 a 3 12
Đáp án A
Gọi H là trọng tâm tam giác ABC
Vì

Đúng 0
Bình luận (0)
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên SA vuông góc với đáy, mặt bên (SBC) tạo với đáy 1 góc bằng
60
∘
. Gọi M, N lần lượt là trung điểm của SB và SC Thể tích V của khối chóp S.AMN? A.
V
a
3
2
B.
V
a
3
4
C.
V...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên SA vuông góc với đáy, mặt bên (SBC) tạo với đáy 1 góc bằng 60 ∘ . Gọi M, N lần lượt là trung điểm của SB và SC Thể tích V của khối chóp S.AMN?
A. V = a 3 2
B. V = a 3 4
C. V = a 3 3 32
D. V = a 3 3 8
Đáp án D
Gọi d là tiếp tuyến của (C) tại điểm A(1:0).
Ta có: y ' = 3 x 2 − 6 x ⇒ y ' 1 = 3.
Suy ra: d : − 3 x − 1 + 0 ⇔ y = − 3 x + 3.
Đúng 0
Bình luận (0)
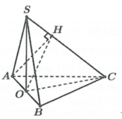
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 1, mặt bên SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với mặt đáy (ABC). Gọi H là hình chiếu vuông góc của A lên SC. Biết . Thể tích của khối chóp S.ABC bằng A.
3
2
B.
3
4
C.
3
6
D.
3
12
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 1, mặt bên SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với mặt đáy (ABC). Gọi H là hình chiếu vuông góc của A lên SC. Biết . Thể tích của khối chóp S.ABC bằng
A. 3 2
B. 3 4
C. 3 6
D. 3 12