\(x-5=\frac{1}{3\left(x+2\right)}\left(đkxđ:x\ne-2\right)\)

\(< =>3\left(x-5\right)\left(x+2\right)=1\)

\(< =>3\left(x^2-3x-10\right)=1\)

\(< =>x^2-3x-10=\frac{1}{3}\)

\(< =>x^2-3x-\frac{31}{3}=0\)

giải pt bậc 2 dễ r

\(\frac{x}{3}+\frac{x}{4}=\frac{x}{5}-\frac{x}{6}\)

\(< =>\frac{4x+3x}{12}=\frac{6x-5x}{30}\)

\(< =>\frac{7x}{12}=\frac{x}{30}< =>12x=210x\)

\(< =>x\left(210-12\right)=0< =>x=0\)

\(3x\left(2x-3\right)-3\left(3+2x^2\right)=0\)

\(< =>6x^2-9x-9-6x^2=0\)

\(< =>-9x-9=0< =>9x+9=0\)

\(< =>x=-\frac{9}{9}=-1\)

Tham khảo:

a) Vẽ đường thẳng \(\Delta : - 2x + y - 1 = 0\) đi qua hai điểm \(A(0;1)\) và \(B\left( { - 1; - 1} \right)\)

Xét gốc tọa độ \(O(0;0).\) Ta thấy \(O \notin \Delta \) và \( - 2.0 + 0 - 1 =  - 1 < 0\)

Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng kể cả bờ \(\Delta \), chứa gốc tọa độ O

(miền không gạch chéo trên hình)

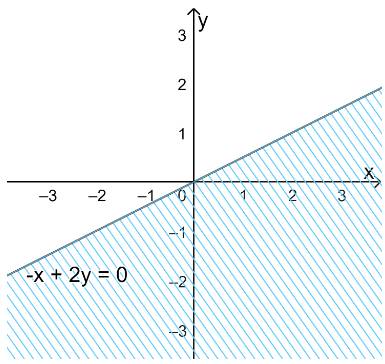
b) Vẽ đường thẳng \(\Delta : - x + 2y = 0\) đi qua hai điểm \(O(0;0)\) và \(B\left( {2;1} \right)\)

Xét điểm \(A(1;0).\) Ta thấy \(A \notin \Delta \) và \( - 1 + 2.0 =  - 1 < 0\)

Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng không kể bờ \(\Delta \), không chứa điểm A (1;0)

(miền không gạch chéo trên hình)

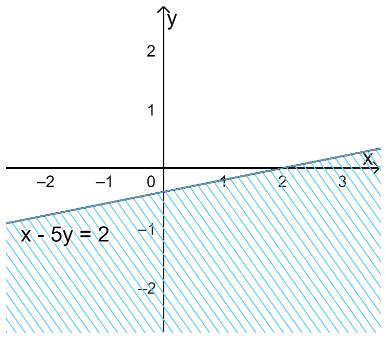
c) Vẽ đường thẳng \(\Delta :x - 5y = 2\) đi qua hai điểm \(A(2;0)\) và \(B\left( { - 3; - 1} \right)\)

Xét gốc tọa độ \(O(0;0).\) Ta thấy \(O \notin \Delta \) và \(0 - 5.0 = 0 < 2\)

Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng không kể bờ \(\Delta \), chứa gốc tọa độ O

(miền không gạch chéo trên hình)

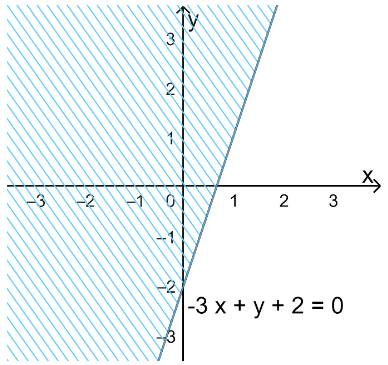
d) Vẽ đường thẳng \(\Delta : - 3x + y + 2 = 0\) đi qua hai điểm \(A(0; - 2)\) và \(B\left( {1;1} \right)\)

Xét điểm \(O(0;0).\) Ta thấy \(O \notin \Delta \) và \( - 3.0 + 0 + 2 = 2 > 0\)

Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng kể cả bờ \(\Delta \), không chứa điểm O (0;0)

(miền không gạch chéo trên hình)

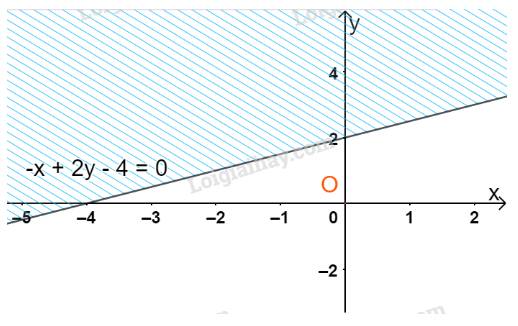
e) Ta có:  \(3(x - 1) + 4(y - 2) < 5x - 3 \Leftrightarrow  - 2x + 4y - 8 < 0 \Leftrightarrow  - x + 2y - 4 < 0\)

Vẽ đường thẳng \(\Delta : - x + 2y -4 = 0\) đi qua hai điểm \(A(0;2)\) và \(B\left( {-4;0} \right)\)

Xét điểm \(O(0;0).\) Ta thấy \(O \notin \Delta \) và \( - 0 + 2.0 -4 = -4 < 0\)

Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng không kể bờ \(\Delta \), chứa điểm O (0;0)

(miền không gạch chéo trên hình)

b: \(\left\{{}\begin{matrix}3x-2y=4\\2x+y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x-2y=4\\4x+2y=10\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}-x=-6\\2x+y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=6\\y=5-2x=5-12=-7\end{matrix}\right.\)

Câu 1: Cặp số là nghiệm phương của 2x + 3y = 7 là:

C. ( 2;1 )

Câu 2: Phương trình x + 2y = 3, Cặp số là nghiệm phương của phương trình đã cho là cặp số : ( 1;1)

1:

a: 2x-3=5

=>2x=8

=>x=4

b: (x+2)(3x-15)=0

=>(x-5)(x+2)=0

=>x=5 hoặc x=-2

2:

b: 3x-4<5x-6

=>-2x<-2

=>x>1

c: =>2x+4>=2x+2-3

=>4>=-1(luôn đúng)

a: 5x+10>3x+3

=>2x>-7

=>x>-7/2

bạn coi lại đề nhé!

a: =>x+2<=0

=>x<=-2

b: =>-x>-1

=>x<1

c: =>2x+4>=2x+2-3

=>4>=-1(luôn đúng)

d: =>2x+2<5x-10-3x

=>2x+2<2x-10

=>2<-10(loại)

Câu 1: 

a) Ta có: \(x^4+3x^2-4=0\)

\(\Leftrightarrow x^4+4x^2-x^2-4=0\)

\(\Leftrightarrow x^2\left(x^2+4\right)-\left(x^2+4\right)=0\)

\(\Leftrightarrow\left(x^2+4\right)\left(x^2-1\right)=0\)

mà \(x^2+4>0\forall x\)

nên \(x^2-1=0\)

\(\Leftrightarrow x^2=1\)

hay \(x\in\left\{1;-1\right\}\)

Vậy: S={1;-1}

Câu 1: 

b) Ta có: \(\left\{{}\begin{matrix}x+2y=5\\x-5y=-9\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}7y=14\\x+2y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=2\\x=5-2y=1\end{matrix}\right.\)

Vậy: (x,y)=(1;2)

Câu 2: 

a) Thay x=-2 vào (d), ta được:

\(y=-2\cdot\left(-2\right)-6=4-6=-2\)

Vậy: T(-2;-2) thuộc (d)

a) Hai mặt phẳng cắt nhau, vì 1: 2: (-1) ≠ 2: 3: (-7)

b) Hai mặt phẳng cắt nhau, vì: 1: (-2): 1 ≠ 2: (-1): 4

c) Hai mặt phẳng song song, vì: 1/2=1/2=1/2 ≠ -1/3

d) Hai mạt phẳng cắt nhau, vì: 3: (-2): 3 ≠ 9: (-6): (-9)

e) Hai mặt phẳng trung nhau, vì: 1/10=-1/(-10)=2/20=-4/(-40).

           #rin

\(a,\Leftrightarrow\left\{{}\begin{matrix}5x+15y=-10\\5x-4y=11\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}19y=-21\\5x-4y=11\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=-\dfrac{21}{19}\\5x-4\left(-\dfrac{21}{19}\right)=11\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{25}{19}\\y=-\dfrac{21}{19}\end{matrix}\right.\)

\(c,\Leftrightarrow\left\{{}\begin{matrix}3x+5y=1\\10x-5y=-40\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x+5y=1\\13x=-39\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-3\\y=2\end{matrix}\right.\\ d,\Leftrightarrow\left\{{}\begin{matrix}5x-10y=-30\\5x-3y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5x-3y=5\\-7y=-35\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=4\\y=5\end{matrix}\right.\\ e,\Leftrightarrow\left\{{}\begin{matrix}2\left(x+y\right)+3\left(x-y\right)=4\\2\left(x+y\right)+4\left(x-y\right)=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-y=6\\2\left(x+y\right)+3\cdot6=4\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x-y=6\\x+y=-7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{2}\\y=-\dfrac{13}{2}\end{matrix}\right.\)