Giải phương trình (đặt ẩn phụ)
(x2 + x )2 + 4(x2 + x )2 - 12 = 0

Những câu hỏi liên quan
Gi ải các phương trình sau (Đặt ẩn phụ)
a)( x2+x)2+4(x2+x)-12=0
b) (x2+2x+3)-9(x2+2x+3)+18=0
c) (x-2)(x+2)(x2-10)=72
a: Đặt \(a=x^2+x\)
Phương trình ban đầu sẽ trở thành \(a^2+4a-12=0\)
=>\(a^2+6a-2a-12=0\)
=>a(a+6)-2(a+6)=0
=>(a+6)(a-2)=0
=>\(\left(x^2+x+6\right)\left(x^2+x-2\right)=0\)
=>\(x^2+x-2=0\)(Vì \(x^2+x+6=\left(x+\dfrac{1}{2}\right)^2+\dfrac{23}{4}>0\forall x\))
=>\(\left(x+2\right)\left(x-1\right)=0\)
=>\(\left[{}\begin{matrix}x+2=0\\x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=1\end{matrix}\right.\)
b:
Sửa đề: \(\left(x^2+2x+3\right)^2-9\left(x^2+2x+3\right)+18=0\)
Đặt \(b=x^2+2x+3\)
Phương trình ban đầu sẽ trở thành \(b^2-9b+18=0\)
=>\(b^2-3b-6b+18=0\)
=>b(b-3)-6(b-3)=0
=>(b-3)(b-6)=0
=>\(\left(x^2+2x+3-3\right)\left(x^2+2x+3-6\right)=0\)
=>\(\left(x^2+2x\right)\left(x^2+2x-3\right)=0\)
=>\(x\left(x+2\right)\left(x+3\right)\left(x-1\right)=0\)
=>\(\left[{}\begin{matrix}x=0\\x+2=0\\x+3=0\\x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-2\\x=-3\\x=1\end{matrix}\right.\)
c: \(\left(x-2\right)\left(x+2\right)\left(x^2-10\right)=72\)
=>\(\left(x^2-4\right)\left(x^2-10\right)=72\)
=>\(x^4-14x^2+40-72=0\)
=>\(x^4-14x^2-32=0\)
=>\(\left(x^2-16\right)\left(x^2+2\right)=0\)
=>\(x^2-16=0\)(do x2+2>=2>0 với mọi x)
=>x2=16
=>x=4 hoặc x=-4
Đúng 1
Bình luận (0)
Giải các phương trình sau bằng cách đặt ẩn số phụ x 2 + 3 x - 1 2 +2( x 2 +3x -1) -8 =0
Đặt m = x 2 +3x -1
Ta có: x 2 + 3 x - 1 2 +2( x 2 +3x -1) -8 =0 ⇔ m 2 +2m -8 =0
∆ ’ = 1 2 -1.(-8) =1 +8 =9 > 0
∆ ' = 9 =3
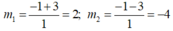
Với m = 2 thì : x 2 +3x - 1 = 2 ⇔ x 2 + 3x - 3 = 0
∆ ’ = 3 2 -4.1.(-3 )=9 +12=21 > 0
∆ ' = 21
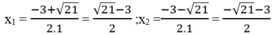
Với m = -4 ta có: x 2 +3x -1 = -4 ⇔ x 2 +3x +3 = 0
∆ = 3 2 -4.1.3=9 -12 = -3 < 0
Phương trình vô nghiệm
Vậy phương trình đã cho có 2 nghiệm :
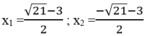
Đúng 0
Bình luận (0)
Giải phương trình bằng cách đặt ẩn phụ: 3 . x 2 + x 2 - 2 x 2 + x - 1 = 0
3.(x2 + x)2 – 2(x2 + x) – 1 = 0 (1)
Đặt t = x2 + x,
Khi đó (1) trở thành : 3t2 – 2t – 1 = 0 (2)
Giải (2) : Có a = 3 ; b = -2 ; c = -1
⇒ a + b + c = 0
⇒ (2) có hai nghiệm t1 = 1; t2 = c/a = -1/3.
+ Với t = 1 ⇒ x2 + x = 1 ⇔ x2 + x – 1 = 0 (*)
Có a = 1; b = 1; c = -1 ⇒ Δ = 12 – 4.1.(-1) = 5 > 0
(*) có hai nghiệm
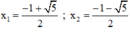
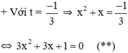
Có a = 3; b = 3; c = 1 ⇒ Δ = 32 – 4.3.1 = -3 < 0
⇒ (**) vô nghiệm.
Vậy phương trình (1) có tập nghiệm 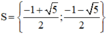
Đúng 0
Bình luận (0)
Giải các phương trình sau bằng phương pháp đặt ẩn phụ: x 2 - 2 x 2 – 2 x 2 + 4x – 3 = 0
Đặt m = x 2 – 2x
Ta có: x 2 - 2 x 2 – 2 x 2 + 4x – 3 = 0
⇔ x 2 - 2 x 2 – 2( x 2 – 2x) – 3 = 0
⇔ m 2 – 2m – 3 = 0
Phương trình m 2 – 2m – 3 = 0 có hệ số a = 1, b = -2, c = -3 nên có dạng a – b + c = 0
Suy ra: m 1 = -1, m 2 = 3
Với m = -1 ta có: x 2 – 2x = -1 ⇔ x 2 – 2x + 1 = 0
Phương trình x 2 – 2x + 1 = 0 có hệ số a = 1, b = -2, c = 1 nên có dạng a + b + c = 0
Suy ra: x 1 = x 2 = 1
Với m = 3 ta có: x 2 – 2x = 3 ⇔ x 2 – 2x – 3 = 0
Phương trình x 2 – 2x – 3 = 0 có hệ số a = 1, b = -2, c = -3 nên có dạng a – b + c = 0
Suy ra: x 1 = -1, x 2 = 3
Vậy phương trình đã cho có 3 nghiệm: x 1 = 1, x 2 = -1, x 3 = 3
Đúng 0
Bình luận (0)
Giải phương trình bằng cách đặt ẩn phụ: x 2 - 4 x + 2 2 + x 2 - 4 x - 4 = 0
(x2 – 4x + 2)2 + x2 – 4x – 4 = 0
⇔ (x2 – 4x + 2)2 + x2 – 4x + 2 – 6 = 0 (1)
Đặt x2 – 4x + 2 = t,
Khi đó (1) trở thành: t2 + t – 6 = 0 (2)
Giải (2): Có a = 1; b = 1; c = -6
⇒ Δ = 12 – 4.1.(-6) = 25 > 0
⇒ (2) có hai nghiệm
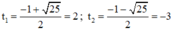
+ Với t = 2 ⇒ x2 – 4x + 2 = 2
⇔ x2 – 4x = 0
⇔ x(x – 4) = 0
⇔ x = 0 hoặc x = 4.
+ Với t = -3 ⇒ x2 – 4x + 2 = -3
⇔ x2 – 4x + 5 = 0 (*)
Có a = 1; b = -4; c = 5 ⇒ Δ’ = (-2)2 – 1.5 = -1 < 0
⇒ (*) vô nghiệm.
Vậy phương trình ban đầu có tập nghiệm S = {0; 4}.
Đúng 0
Bình luận (0)
Giải các phương trình sau bằng phương pháp đặt ẩn phụ: 3 x 2 + x + 1 – x = x 2 + 3
Giải phương trình bằng cách đặt ẩn phụ:
a
)
3.
x
2
+
x
2
−
2
x
2
+
x...
Đọc tiếp
Giải phương trình bằng cách đặt ẩn phụ:
a ) 3. x 2 + x 2 − 2 x 2 + x − 1 = 0 b ) x 2 − 4 x + 2 2 + x 2 − 4 x − 4 = 0 c ) x − x = 5 x + 7 d ) x x + 1 − 10 ⋅ x + 1 x = 3
a)
3 · x 2 + x 2 - 2 x 2 + x - 1 = 0 ( 1 )
Đặt t = x 2 + x ,
Khi đó (1) trở thành : 3 t 2 – 2 t – 1 = 0 ( 2 )
Giải (2) : Có a = 3 ; b = -2 ; c = -1
⇒ a + b + c = 0
⇒ (2) có hai nghiệm t 1 = 1 ; t 2 = c / a = - 1 / 3 .
+ Với t = 1 ⇒ x 2 + x = 1 ⇔ x 2 + x – 1 = 0 ( * )
Có a = 1; b = 1; c = -1 ⇒ Δ = 1 2 – 4 . 1 . ( - 1 ) = 5 > 0
(*) có hai nghiệm
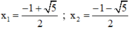
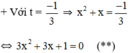
Có a = 3; b = 3; c = 1 ⇒ Δ = 3 2 – 4 . 3 . 1 = - 3 < 0
⇒ (**) vô nghiệm.
Vậy phương trình (1) có tập nghiệm 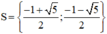
b)
x 2 − 4 x + 2 2 + x 2 − 4 x − 4 = 0 ⇔ x 2 − 4 x + 2 2 + x 2 − 4 x + 2 − 6 = 0 ( 1 )
Đặt x 2 – 4 x + 2 = t ,
Khi đó (1) trở thành: t 2 + t – 6 = 0 ( 2 )
Giải (2): Có a = 1; b = 1; c = -6
⇒ Δ = 1 2 – 4 . 1 . ( - 6 ) = 25 > 0
⇒ (2) có hai nghiệm
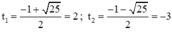
+ Với t = 2 ⇒ x 2 – 4 x + 2 = 2
⇔ x 2 – 4 x = 0
⇔ x(x – 4) = 0
⇔ x = 0 hoặc x = 4.
+ Với t = -3 ⇒ x 2 – 4 x + 2 = - 3
⇔ x2 – 4x + 5 = 0 (*)
Có a = 1; b = -4; c = 5 ⇒ Δ ’ = ( - 2 ) 2 – 1 . 5 = - 1 < 0
⇒ (*) vô nghiệm.
Vậy phương trình ban đầu có tập nghiệm S = {0; 4}.
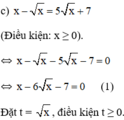
Khi đó (1) trở thành: t 2 – 6 t – 7 = 0 ( 2 )
Giải (2): Có a = 1; b = -6; c = -7
⇒ a – b + c = 0
⇒ (2) có nghiệm t 1 = - 1 ; t 2 = - c / a = 7 .
Đối chiếu điều kiện chỉ có nghiệm t = 7 thỏa mãn.
+ Với t = 7 ⇒ √x = 7 ⇔ x = 49 (thỏa mãn).
Vậy phương trình đã cho có nghiệm x = 49.
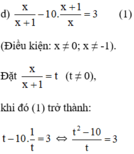
⇔ t 2 – 10 = 3 t ⇔ t 2 – 3 t – 10 = 0 ( 2 )
Giải (2): Có a = 1; b = -3; c = -10
⇒ Δ = ( - 3 ) 2 - 4 . 1 . ( - 10 ) = 49 > 0
⇒ (2) có hai nghiệm:
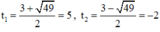
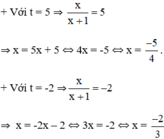
Cả hai nghiệm đều thỏa mãn điều kiện xác định.
Vậy phương trình đã cho có tập nghiệm 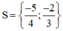
Đúng 0
Bình luận (0)
Giải các phương trình sau bằng cách đặt ẩn số phụ 2 x 2 + x - 2 2 +10 x 2 +5x -16 =0
Đặt m = 2 x 2 +x -2
Ta có: 2 x 2 + x - 2 2 +10 x 2 +5x -16 =0
⇔ 2 x 2 + x - 2 2 +5(2 x 2 +x -2) -6 =0
⇔ m 2 +5m -6 =0
Phương trình m 2 +5m -6 = 0 có hệ số a = 1, b = 5, c = -6 nên có dạng
a + b + c = 0
Suy ra : m 1 =1 , m 2 =-6
m1 =1 ta có: 2 x 2 +x -2 =1 ⇔ 2 x 2 +x -3=0
Phương trình 2 x 2 +x -3 = 0 có hệ số a = 2, b = 1 , c = -3 nên có dạng
a +b+c=0
Suy ra: x 1 =1 , x 2 =-3/2
Với m=-6 ta có: 2 x 2 +x -2 = -6 ⇔ 2 x 2 +x +4 =0
∆ = 1 2 -4.2.4 = 1 -32 = -31 < 0 . Phương trình vô nghiệm
Vậy phương trình đã cho có 2 nghiệm : x 1 =1 , x 2 =-32
Đúng 0
Bình luận (0)
Giải các phương trình sau bằng cách đặt ẩn số phụ ( x 2 -3x +4)( x 2 -3x +2) =3
Đặt m= x 2 -3x +2
Ta có: ( x 2 -3x +4)( x 2 -3x +2) =3
⇔ [( x 2 -3x +2 +2)( x 2 -3x +2) -3 =0
⇔ x 2 - 3 x + 2 2 +2( x 2 -3x +2) -3 =0
⇔ m 2 +2m -3 =0
Phương trình m 2 +2m -3 = 0 có hệ số a = 1, b = 2 , c = -3 nên có dạng
a +b+c=0
suy ra : m 1 =1 , m 2 =-3
Với m 1 =1 ta có: x 2 -3x +2 =1 ⇔ x 2 -3x +1=0
∆ = - 3 2 -4.1.1 = 9 -4 =5 > 0
∆ = 5
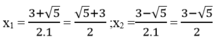
Với m 2 =-3 ta có: x 2 -3x +2 =-3 ⇔ x 2 -3x +5=0
∆ = - 3 2 -4.1.5 = 9 -20 =-11 < 0.Phương trình vô nghiệm
Vậy phương trình đã cho có 2 nghiệm :
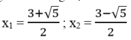
Đúng 0
Bình luận (0)
Giải các phương trình sau (Đặt ẩn phụ)
d) x(x+1)(x2+x+1)=42
e) (x-1)(x-3)(x+5)(x+7)-297=0
f) x4-2x2-144x-1295=0
d: \(x\left(x+1\right)\left(x^2+x+1\right)=42\left(1\right)\)
=>\(\left(x^2+x\right)\left(x^2+x+1\right)=42\)
Đặt \(a=x^2+x\)
Phương trình (1) sẽ trở thành \(a\left(a+1\right)=42\)
=>\(a^2+a-42=0\)
=>(a+7)(a-6)=0
=>\(\left(x^2+x+7\right)\left(x^2+x-6\right)=0\)
mà \(x^2+x+7=\left(x+\dfrac{1}{2}\right)^2+\dfrac{27}{4}>0\forall x\)
nên \(x^2+x-6=0\)
=>(x+3)(x-2)=0
=>\(\left[{}\begin{matrix}x+3=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=2\end{matrix}\right.\)
e: \(\left(x-1\right)\left(x-3\right)\left(x+5\right)\left(x+7\right)-297=0\left(2\right)\)
=>\(\left(x-1\right)\left(x+5\right)\left(x-3\right)\left(x+7\right)-297=0\)
=>\(\left(x^2+4x-5\right)\left(x^2+4x-21\right)-297=0\)
Đặt \(b=x^2+4x\)
Phương trình (2) sẽ trở thành \(\left(b-5\right)\left(b-21\right)-297=0\)
=>\(b^2-26b+105-297=0\)
=>\(b^2-26b-192=0\)
=>(b-32)(b+6)=0
=>\(\left(x^2+4x-32\right)\left(x^2+4x+6\right)=0\)
mà \(x^2+4x+6=\left(x+2\right)^2+2>0\forall x\)
nên \(x^2+4x-32=0\)
=>(x+8)(x-4)=0
=>\(\left[{}\begin{matrix}x+8=0\\x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-8\\x=4\end{matrix}\right.\)
f: \(x^4-2x^2-144x-1295=0\)
=>\(x^4-7x^3+7x^3-49x^2+47x^2-329x+185x-1295=0\)
=>\(\left(x-7\right)\cdot\left(x^3+7x^2+47x+185\right)=0\)
=>\(\left(x-7\right)\left(x+5\right)\left(x^2+2x+37\right)=0\)
mà \(x^2+2x+37=\left(x+1\right)^2+36>0\forall x\)
nên (x-7)(x+5)=0
=>\(\left[{}\begin{matrix}x-7=0\\x+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=7\\x=-5\end{matrix}\right.\)
Đúng 1
Bình luận (0)







