Chứng minh tính đơn điệu của tan luôn đồng biến trên tập xác định

Những câu hỏi liên quan
Dùng định nghĩa xét tính đơn điệu của hàm số y=\(\dfrac{m+1}{x}\) đồng biến trên từng khoảng xác định.
Chứng minh tính đơn điệu của hàm số y=cos x đồng biến trên khoảng \(\left(-\pi+k2\pi;0+k2\pi\right)\)
Cho hàm số y=(m2 -2m+3)x - 4 (d)
chứng minh rằng với mọi m hàm số luôn đồng biến trên tập xác định của nó
Hàm số nào sau đây luôn đồng biến trên tập xác định của nó A.
y
x
−
1
2
−
x
B.
y
1
−
2
x
1
−
x
C.
y...
Đọc tiếp
Hàm số nào sau đây luôn đồng biến trên tập xác định của nó
A. y = x − 1 2 − x
B. y = 1 − 2 x 1 − x
C. y = x + 1 2 x + 1
D. y = 2 x x − 1
Đáp án C
Gọi I là trung điểm của BC. Ta có:
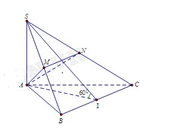

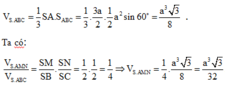
Đúng 0
Bình luận (0)
Chứng minh tính đơn điệu của hàm số y=sin x đồng biến trên khoảng (\(\dfrac{-\pi}{2}+k2\pi;\dfrac{\pi}{2}+k2\pi\)) và nghịch biến trên khoảng (\(\dfrac{\pi}{2}+k2\pi;\dfrac{3\pi}{2}+k2\pi\))
Trên \(\left(-\dfrac{\pi}{2}+k.2\pi;\dfrac{\pi}{2}+k.2\pi\right)\) chọn 2 giá trị của x (x1 và x2) sao cho x1 > x2
Xét f(x1) - f(x2) = sinx1 - sinx2
= 2cos\(\dfrac{x_1+x_2}{2}\) . sin \(\dfrac{x_1-x_2}{2}\)
Do \(\dfrac{x_1+x_2}{2}\in\left(0;\dfrac{\pi}{2}\right)\)
⇒ cos\(\dfrac{x_1+x_2}{2}\) > 0
Mà \(sin\dfrac{x_1-x_2}{2}\) > 0
nên f(x1) - f(x2) > 0
Vậy đồng biến
Nghịch biến tương tự
Đúng 0
Bình luận (4)
Cho hàm số y = m x - 1 2 x + m
Chứng minh rằng với mọi giá trị của tham số m, hàm số luôn đồng biến trên khoảng xác định của nó.
Với mọi tham số m ta có :
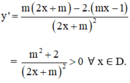
Vậy hàm số luôn đồng biến trên mỗi khoảng xác định của nó.
Đúng 0
Bình luận (0)
Cho hàm số: y = –( m 2 + 5m) x 3 + 6m x 2 + 6x – 5. Xác định m để hàm số đơn điệu trên R. Khi đó, hàm số đồng biến hay nghịch biến? Tại sao?
y = –( m 2 + 5m) x 3 + 6m x 2 + 6x – 5
y′ = –3( m 2 + 5m) x 2 + 12mx + 6
Hàm số đơn điệu trên R khi và chỉ khi y’ không đổi dấu.
Ta xét các trường hợp:
+)
m
2
+ 5m = 0 ⇔ 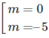
– Với m = 0 thì y’ = 6 nên hàm số luôn đồng biến.
– Với m = -5 thì y’ = -60x + 6 đổi dấu khi x đi qua .
+) Với m 2 + 5m ≠ 0. Khi đó, y’ không đổi dấu nếu
∆ ' = 36 m 2 + 18( m 2 + 5m) ≤ 0 ⇔ 3 m 2 + 5m ≤ 0 ⇔ –5/3 ≤ m ≤ 0
– Với điều kiện đó, ta có –3( m 2 + 5m) > 0 nên y’ > 0 và do đó hàm số đồng biến trên R.
Vậy với điều kiện –5/3 ≤ m ≤ 0 thì hàm số đồng biến trên R.
Đúng 0
Bình luận (0)
Định nghĩa sự đơn điệu ( đồng biến, nghịch biến) của một hàm số trên một khoảng.
Cho hàm số y = f(x) xác định trên khoảng K, hàm số f(x) được gọi là
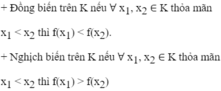
Hàm số chỉ đồng biến hoặc nghịch biến trên K gọi là đơn điệu trên K
Đúng 0
Bình luận (0)
Cho
y
m
x
2
−
m
+
2
x
+
m
2
−
2
m
+
2
x
−
1...
Đọc tiếp
Cho y = m x 2 − m + 2 x + m 2 − 2 m + 2 x − 1 . Tìm m để hàm số luôn đồng biến trên tập xác định của nó
A. 0 < m ≤ 2
B. 1 < m ≤ 2
C. 0 < m ≤ 1
D. m < 0 m > 3
Đáp án A
T X D : D = ℝ \ 1
Ta có: y = m x 2 − m + 2 x + m 2 − 2 m + 2 x − 1 = m x − 2 + m 2 − 2 m x − 1 ⇒ y ' = m − m 2 − 2 m x − 1 2
hàm số luôn đồng biến trên tập xác định của nó khi y ' ≥ 0 ∀ x ∈ D (dấu bằng xảy ra tại hữu hạn điểm)
⇔ m − m 2 − 2 m x − 1 2 ≥ 0 ∀ x ∈ D ⇔ x x − 1 2 ≥ m 2 − 2 m ∀ x ∈ D
Với m = 0 ⇒ y ' = 0 ∀ x ∈ D (không thỏa mãn dấu bằng xảy ra tại hữu hạn điểm)
Khi đó hàm số luôn đồng biến trên tập xác định m > 0 m 2 − 2 m ≤ 0 ⇔ 0 < m ≤ 2
Đúng 0
Bình luận (0)







