Cho tam giác đều ABC, đường cao AH. M là một điểm bất kỳ trên cạnh BC. Vẽ MP vuông góc với AC; MQ vuông góc với AB. Gọi O là trung điểm của AM.
a)Tứ OPHQ là hình gì? Chứng minh.
b) Xác định vị trí của M trên cạnh BC để độ dài PQ nhỏ nhất.

Những câu hỏi liên quan
Cho tam giác ABC đều,đường cao AH, lấy điểm M bất kỳ trong tam giác,vẽ MI vuông góc với AB, MK vuông góc với AC, MN vuông góc với BC Chứng minh rằng AH= MI + MK + MN
bạn tham khảo tại đây nhé:
Câu hỏi của Nguyễn Văn Hòa - Toán lớp 7 - Học toán với OnlineMath
Ta thấy ngay MI + MJ + MK = AH (AH là chiều cao tam giác ABC)
Đúng 0
Bình luận (0)
Cho tam giác ABC đều ,có đường cao AH (H thuộc BC ).Trên cạnh BC lấy điểm M bất kỳ ( M không trùng với B,C,H ) ; gọi P,Q lần lượt là hình chiếu vuông góc của M lên các cạnh AB,AC .
a) CM tứ giác APMQ nội tiếp một đường tròn
b) chứng minh MP +MQ = AH
c) gọi O là tâm đường tròn ngoại tiếp tứ giác APMQ . chứng minh OH vuông góc với PQ ?
A) MP vuông góc AB tại P => góc MPA=90; MQ vuông góc AC tại Q=> MQA=90
=> tg APMQ nội tiếp(tổng 2 góc đối =90)
b) diện tích tam giác AMB=1/2.MP.AB=1/2.MP.BC; diện tích tam giác AMC=1/2.MQ.AC=1/2.MP.BC( AB=BC=CA tam giác đều)
S tam giác ABC=1/2.AH.BC
ta có: S AMB+S AMC=S ABC <=> \(\frac{1}{2}.MP.BC+\frac{1}{2}MQ.BC=\frac{1}{2}AH.BC\Leftrightarrow\frac{1}{2}BC\left(MP+MQ\right)=\frac{1}{2}.BC.AH\)
=> MP+MQ=AH
c) góc AHM=90(AH là đường cao)=> H cũng thuộc đường tròn đường kính AM <=> ngũ giác APMQH nội tiếp
(O): góc HAQ=1/2 góc HOQ(góc nt và góc ở tâm)
tam giác AHC vuông => góc HAC=90-C=90-60=30 độ hay HAQ=30(góc C=60 vì tam giác đều)
=> góc HOQ=2.30=60 .
(O): góc PAQ=1/2 góc POQ(góc nt và góc ở tâm) <=> góc POQ=2.60=120( góc PAQ hay BAC=60- tam giác đều)
góc HOQ=60 => OH là pg của góc POQ.
tam giác POQ có: OP=OQ=R=> tam giác cân => OH đồng thời là đường cao => OH vuông góc PQ
Đúng 1
Bình luận (0)
câu a , tổng hai góc đối là 180 độ nhé bạn
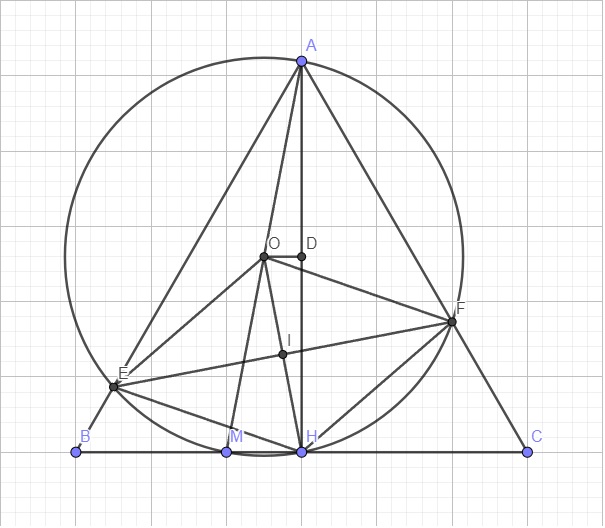
Cho tam giác đều ABC cạnh a với đường cao AH. M là 1 điểm bất kì trên cạnh BC. Vẽ ME vuông góc AB, MF vuông góc AC. Gọi O là trung điểm của AM.
a). CM rằng 5 đ A, E, H, M, F cùng nằm trên cùng một đường tròn.
b). Tứ giác OEHF là hình gì.
c). Tìm GTNN của diện tích tứ giác OEHF theo a khi M di động trên cạnh BC.
(Nếu được thì giải chi tiết câu (c) giúp em em cảm ơn ạ)
a. Em tự giải
b. Do tam giác ABC đều và AH là đường cao \(\Rightarrow AH\) đồng thời là phân giác góc A
\(\Rightarrow\widehat{BAH}=\widehat{CAH}=\dfrac{1}{2}\widehat{A}=\dfrac{1}{2}.60^0=30^0\)
AEMHF nội tiếp đường tròn tâm O \(\Rightarrow\widehat{HOF}=2.\widehat{CAH}=60^0\) (góc nội tiếp và góc ở tâm cùng chắn cung HF)
Mà \(OH=OF\) (cùng là bán kính) \(\Rightarrow\Delta OHF\) đều (tam giác cân có 1 góc 60 độ)
Tương tự ta có \(\widehat{HOE}=60^0\Rightarrow\Delta OHE\) đều
\(\Rightarrow OE=OF=HE=HF\Rightarrow OEHF\) là hình thoi
c.
Gọi D là trung điểm AH \(\Rightarrow OD\perp AH\) \(\Rightarrow OH\ge DH\Rightarrow OH\ge\dfrac{1}{2}AH\Rightarrow OH\ge\dfrac{a\sqrt{3}}{2}\)
Gọi I là giao điểm EF và OH \(\Rightarrow I\) là tâm hình thoi OEHF
\(S_{OEHF}=2S_{OHE}=2EI.OH=2\sqrt{OE^2-OI^2}.OH\)
\(=2OH.\sqrt{OH^2-\left(\dfrac{OH}{2}\right)^2}=OH^2\sqrt{3}\ge\left(\dfrac{a\sqrt{3}}{2}\right)^2.\sqrt{3}=\dfrac{3a^2\sqrt{3}}{2}\)
Dấu "=" xảy ra khi \(OH=DH\Leftrightarrow O\) trùng D
\(\Rightarrow M\) trùng H
Đúng 3
Bình luận (4)
Cho tam giác ABC đều, đường cao AH. M là điểm bất kỳ trên đáy BC. Kẻ MP vuông góc AB và MQ vuông góc AC. Gọi O là trung điểm của AM.
a) CM 5 điểm A, P, M, H, Q cùng nằm trên một đường tròn
b) Tứ giác OPQH là hình gì?
c) Xác định vị trì cuả M trên BC để PQ có độ dài nhỏ nhất
Cho tam giác đều ABC, đường cao AH. M là một điểm bất kì trên cạnh BC. Vẽ MP vuông góc với AB.Gọi O là trung điểm của AM.
a, CM A,P,M,H,Q cùng nằm trên cùng 1 đường tròn
b,Tứ giác OPHQ là hình gì.CM
c,Xác định vị trí của M trên cạnh BC để độ dài PQ nhỏ nhất.Tính giá trị nhỏ nhất đó nếu cạnh tam giác đều là a
Cho tam giác $ABC$ đều, có đường cao $AH$ ($H$ thuộc cạnh $BC$). Trên cạnh $BC$ lấy điểm $M$ bất kỳ ($M$ không trùng với $B$, $C$, $H$). Gọi $P$, $Q$ lần lượt là hình chiếu vuông góc của $M$ lên các cạnh $AB$, $AC$.
Xem chi tiết
a) Chứng minh rằng tứ giác $APMQ$ nội tiếp một đường tròn.
Ta có: MP vuông góc AB (gt)
=) Góc MPA = 90độ (1)
Lại có: MQ vuông góc AC (gt)
=) Góc MQA = 90 độ (2)
Từ (1) và (2) =) góc MPA + góc MQA = 180độ
Mà 2 góc ở vị trí đối nhau
=) Tứ giác APMQ nội tiếp
cho tam giác abc vuông tại a đường cao ah từ m là một điểm bất kì trên cạnh bc kẻ md vuông góc với ab, me vuông góc với ac chứng minh 5 điểm a,d,m,h,e cùng nằm trên một đường tròn
cho tam giác abc vuông tại a đường cao ah từ m là một điểm bất kì trên cạnh bc kẻ md vuông góc với ab, me vuông góc với ac chứng minh 5 điểm a,d,m,h,e cùng nằm trên một đường tròn
Cho tam giác ABC đều có đường cao AH. Trên cạnh BC lấy điểm D bất kì. Gọi E là điểm đối xứng D qua AB, F là điểm đối xứng của D qua AC. Kẻ EM vuông góc với BC, FN vuông góc với BC. Cm EM+FN=AH
Cho tam giác ABC có đường cao AH .Trên cạnh BC lấy điểm M bất kì ( M không trùng với B ,C ,H ) từ M kẻ MP và MQ vuông góc với các cạnh AB ,AC
1.Chứng minh APMQ là tứ giác nội tiếp và hãy xác định tâm O của đường tròn ngoại tiếp tứ giác đó .
2.Chứng minh rằng MP+MQ=AH .
3.Chứng minh OH vuông góc với PQ.