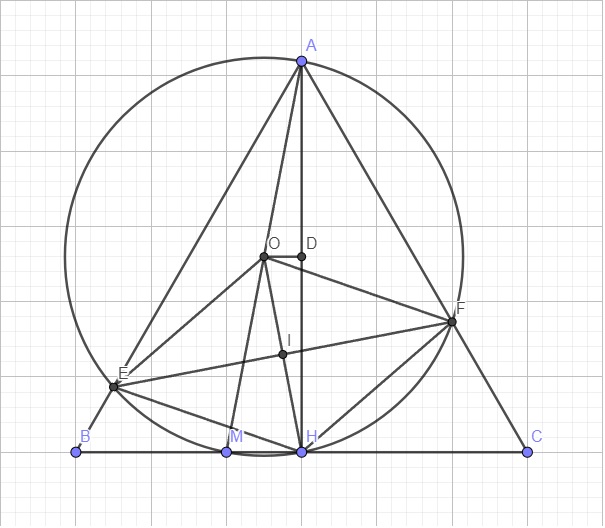
Cho tam giác đều ABC cạnh a với đường cao AH. M là 1 điểm bất kì trên cạnh BC. Vẽ ME vuông góc AB, MF vuông góc AC. Gọi O là trung điểm của AM.
a). CM rằng 5 đ A, E, H, M, F cùng nằm trên cùng một đường tròn.
b). Tứ giác OEHF là hình gì.
c). Tìm GTNN của diện tích tứ giác OEHF theo a khi M di động trên cạnh BC.
(Nếu được thì giải chi tiết câu (c) giúp em em cảm ơn ạ)
a. Em tự giải
b. Do tam giác ABC đều và AH là đường cao \(\Rightarrow AH\) đồng thời là phân giác góc A
\(\Rightarrow\widehat{BAH}=\widehat{CAH}=\dfrac{1}{2}\widehat{A}=\dfrac{1}{2}.60^0=30^0\)
AEMHF nội tiếp đường tròn tâm O \(\Rightarrow\widehat{HOF}=2.\widehat{CAH}=60^0\) (góc nội tiếp và góc ở tâm cùng chắn cung HF)
Mà \(OH=OF\) (cùng là bán kính) \(\Rightarrow\Delta OHF\) đều (tam giác cân có 1 góc 60 độ)
Tương tự ta có \(\widehat{HOE}=60^0\Rightarrow\Delta OHE\) đều
\(\Rightarrow OE=OF=HE=HF\Rightarrow OEHF\) là hình thoi
c.
Gọi D là trung điểm AH \(\Rightarrow OD\perp AH\) \(\Rightarrow OH\ge DH\Rightarrow OH\ge\dfrac{1}{2}AH\Rightarrow OH\ge\dfrac{a\sqrt{3}}{2}\)
Gọi I là giao điểm EF và OH \(\Rightarrow I\) là tâm hình thoi OEHF
\(S_{OEHF}=2S_{OHE}=2EI.OH=2\sqrt{OE^2-OI^2}.OH\)
\(=2OH.\sqrt{OH^2-\left(\dfrac{OH}{2}\right)^2}=OH^2\sqrt{3}\ge\left(\dfrac{a\sqrt{3}}{2}\right)^2.\sqrt{3}=\dfrac{3a^2\sqrt{3}}{2}\)
Dấu "=" xảy ra khi \(OH=DH\Leftrightarrow O\) trùng D
\(\Rightarrow M\) trùng H