Cho △ABC, M là trung điểm của BC , AM= 1/2 BC .
Chứng minh : \(\widehat{BAC}=90^o\)

Những câu hỏi liên quan
Cho tam giác ABC có ABAC, M là trung điểm BC
a)Chứng minh AM là tia phân giác của widehat{BAC} (khỏi cần làm nha)
b)Chứng minh AMperp BC(khỏi cần luôn)
c)Trên tia đối của BC lấy điểm P, trên tia đối của CB lấy điểm N sao cho BPCN. Chứng minh APAN
D)Gọi E là trung điểm của AB, F là trung điểm của AC, CE và BF cắt nhau tại I. Chứng minh A, I, M thẳng hàng.
(mọi người giúp mình câu c,d với ạ ko cần vẽ hình nha! cảm ơn mọi người nhiềuu)
Đọc tiếp
Cho tam giác ABC có AB=AC, M là trung điểm BC
a)Chứng minh AM là tia phân giác của \(\widehat{BAC}\) (khỏi cần làm nha)
b)Chứng minh \(AM\perp BC\)(khỏi cần luôn)
c)Trên tia đối của BC lấy điểm P, trên tia đối của CB lấy điểm N sao cho BP=CN. Chứng minh AP=AN
D)Gọi E là trung điểm của AB, F là trung điểm của AC, CE và BF cắt nhau tại I. Chứng minh A, I, M thẳng hàng.
(mọi người giúp mình câu c,d với ạ ko cần vẽ hình nha! cảm ơn mọi người nhiềuu)
cho tam giác ABC có M là trung điểm của BC .chứng minh rằng :
a) AM >1/2 BC thì góc BAC <90
b) AM <1/2BC thì góc BAC >90
c) AM=1/2BC thì góc BAC =90
cho tam giác ABC có ABAC M là trung điểm của BC Chứng minh AM là phân giác của góc BAC chứng minh AM vuông góc với BC chứng minh M là trung điểm của AN
Đọc tiếp
cho tam giác ABC có AB=AC M là trung điểm của BC Chứng minh AM là phân giác của góc BAC chứng minh AM vuông góc với BC chứng minh M là trung điểm của AN
Bài 1 : Cho tam giác ABC, điểm D thuộc cạnh AC sao cho AD1/2 DC. Gọi M là trung điểm của BC , I là giao điểm của BD và AM . Chứng minh AIAMbài 2: Cho hình thang vuông ABCD ( widehat{A}widehat{D}90^o) có I là trung điểm của BC . Chứng minh rằng tam giác IAD cânxin hãy giúp mình thật nhanh mình đang cần raất gấp
Đọc tiếp
Bài 1 : Cho tam giác ABC, điểm D thuộc cạnh AC sao cho AD=1/2 DC. Gọi M là trung điểm của BC , I là giao điểm của BD và AM . Chứng minh AI=AM
bài 2: Cho hình thang vuông ABCD ( \(\widehat{A}\)\(=\widehat{D}\)\(=90^o\)) có I là trung điểm của BC . Chứng minh rằng tam giác IAD cân
xin hãy giúp mình thật nhanh
mình đang cần raất gấp
Cho tam giác ABC, gọi M là trung điểm của cạnh BC. Qua điểm A kẻ đường thẳng song song với BC và trên đường thẳng đó lấy D sao cho ADAM(M và D nằm khác phía đối với AB)a) Chứng minh Delta ABD DeltaBAMb)Chứng minh AM // BD và AMBDc)Gọi I là trung điểm của đoạn thẳng AM.Chứng minh D,I,C thẳng hàngd)Giả sử BDBM.Chứng minh rằng widehat{BAC} ^{90^o}
Đọc tiếp
Cho tam giác ABC, gọi M là trung điểm của cạnh BC. Qua điểm A kẻ đường thẳng song song với BC và trên đường thẳng đó lấy D sao cho AD=AM(M và D nằm khác phía đối với AB)
a) Chứng minh \(\Delta\) ABD = \(\Delta\)BAM
b)Chứng minh AM // BD và AM=BD
c)Gọi I là trung điểm của đoạn thẳng AM.Chứng minh D,I,C thẳng hàng
d)Giả sử BD=BM.Chứng minh rằng \(\widehat{BAC}\) =\(^{90^o}\)
Bạn tự vẽ hình nha!!!
a.)Xét\(\Delta ABD\)và\(\Delta ABM\)có:
\(AD=BM\)
\(AB:\)Chung
\(\widehat{DAB}=\widehat{ABM}\left(slt\right)\)
\(\Rightarrow\Delta ABD=\Delta BAM\)
b.)Ta có:\(\Delta ABD=\Delta BAM\)(Theo a)
\(\Rightarrow\widehat{DBA}=\widehat{BAM}\)(mà 2 góc SLT)
\(\Rightarrow AM//BD\)
c.)Xét\(\Delta ADI\)và\(\Delta IMC\)có:
\(AD=CM\)
\(\widehat{DAI}=\widehat{IMC}\)
\(AI=IM\)
\(\Rightarrow\Delta AID=\Delta IMC\)
\(\Rightarrow IA=IC\)
\(\Rightarrow I\)là trung điểm của\(AC\)
\(\Rightarrow I,A,C\)thẳng hàng(đpcm)
P/s:#Study well#
Cho tam giác ABC , M là trung điểm của cạnh BC
a) góc A = 90 độ , Chứng minh : AM=1/2 BC
b)góc A > 90 độ . Chứng minh AM < 1/2 BC
c) góc A < 90 độ . Chứng minh AM > 1/2 BC
Tam giác ABC có trung tuyến AM. Chứng minh rằng \(AM>\frac{1}{2}BC\)khi và chỉ khi \(\widehat{BAC}< 90^o\)
Ta có: AM là trung tuyến của \(\Delta ABC\).
- Nếu \(AM>\frac{1}{2}.BC\) \(\Rightarrow AM>BM=CM\).
+) \(AM>BM\Rightarrow\widehat{B}>\widehat{BAM}\Rightarrow\widehat{B}=\widehat{BAM}+x^o\)(1). Tương tự, ta có : \(\widehat{C}=\widehat{MAC}+y^o\)(2)
Lại có: \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)(tổng 3 góc trong 1 tam giác)
Từ (1) và (2) \(\Rightarrow\widehat{A}+\left(\widehat{BAM}+\widehat{MAC}\right)+x^o+y^o=180^o\)
\(\Rightarrow2.\widehat{A}+x^o+y^o=180^o\)
\(\Rightarrow\widehat{A}=\frac{180^o-x^o-y^o}{2}=90^o-\frac{x^o+y^o}{2}< 90^o\)
\(\Rightarrow AM>\frac{1}{2}BC\Leftrightarrow\widehat{BAC}< 90^o\)(đpcm).
P/S: Bạn tự vẽ hình nha ^_^!
Đúng 0
Bình luận (0)
Cho tam giác ABC và M là trung điểm của BC. Biết \(\widehat {AMB} = \widehat {AMC}\). Chứng minh AM là đường trung trực của đoạn thẳng BC.
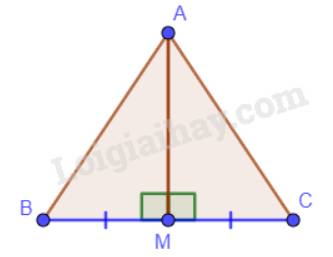
M là trung điểm của BC nên B, M, C thằng hàng → \(\widehat {BMC} = 180^\circ \). Mà \(\widehat {AMB} = \widehat {AMC}\)nên \(\widehat {AMB} = \widehat {AMC} = 180^\circ :2 = 90^\circ \)→ \(AM \bot BC\).
Vậy AM đi qua trung điểm M của đoạn thẳng BC và AM vuông góc với BC. Hay AM là đường trung trực của đoạn thẳng BC.
Đúng 0
Bình luận (0)
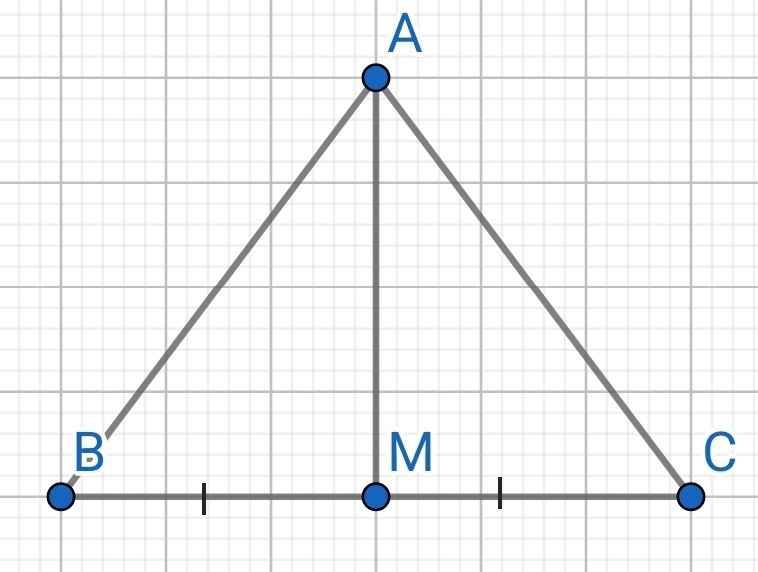 Ta có:
Ta có:
∠AMB + ∠AMC = 180⁰ (kề bù)
Mà ∠AMB = ∠AMC (gt)
⇒ ∠AMB = ∠AMC = 180⁰ : 2 = 90⁰
⇒ AM ⊥ BC
Mà M là trung điểm của BC
⇒ AM là đường trung trực của BC
Đúng 0
Bình luận (0)
cho tam giác abc m là trung điểm của bc chứng minh a) Nếu A = 90 thì AM=1/2 BC b) Nếu AM =1/2BC thì A =90
a) Ke AD sao cho goc DAB =goc ACD => goc DAB =goc BAD ( cung phu voi DAC)
=> tam giac ABD can tai D => AD=BD
=>Tam giac ADC can tai D => AD=DC
=>DB=DC=DA => D trung voi M
=> AM =BC/2
b) Nguoc lai :
Neu AM =BC/2 => AM =MB =MC
=> ABM can tai M ; ACM can tai M
=> BAM + CAM = (180- AMB)/2 +(180-AMC)/2 = (360 -(AMB+AMC))/2 =(360-180)/2=180/2=90
=>BAC=90
=> A=90
Đúng 0
Bình luận (0)



















