Tìm trọng tâm một hình chữ nhật đã bị cắt chéo một nử

Những câu hỏi liên quan
Tìm trọng tâm của hình chữ nhật đã bị cắt một nử ? Vật lí 10
Hãy xác định trọng tâm của một bản phẳng mỏng, đồng chất, hình chữ nhật, dài 12 cm, rộng 6 cm, bị cắt mất một phần hình vuông có cạnh 3 cm ở một góc (Hình 19.7).
Bản phẳng coi như gồm hai bản AHEF và HBCD ghép lại.
Biểu diễn trọng tâm các bản như hình vẽ sau:
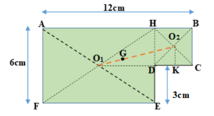
Vì các bản đồng chất, phẳng mỏng đều nên tỉ lệ diện tích bằng tỉ lệ về trọng lượng:
![]()
Gọi G là trọng tâm của cả bản phẳng ⇒ G phải nằm trền đoạn thẳng O1O2, trong đó O1 là trọng tâm của bản AHEF, O2 là trọng tâm của bản HBCD.
Ta có:
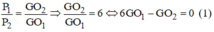
Xét tam giác vuông O1O2K ta có:
![]()
Giải hệ (1) và (2) ta được: GG1 ≈ 0,88 cm
Vậy trọng tâm G của bản phẳng nằm trên đoạn O1O2 cách O1 một đoạn 0,88 cm.
Đúng 0
Bình luận (0)
Hãy xác định trọng tâm của một bản phẳng mỏng, đồng chất, hình chữ nhật, dài 12 cm, rộng 6 cm, bị cắt mất một phần hình vuông có cạnh 3 cm ở một góc (Hình vẽ). Chọn đáp án đúng A. Trọng tâm G của bản phẳng nằm trên đoạn
O
1
O
2
cách
O
1
một đoạn 0,88 cm. B. Trọng tâm G của bản phẳng nằm trên đoạn AE cách
O...
Đọc tiếp
Hãy xác định trọng tâm của một bản phẳng mỏng, đồng chất, hình chữ nhật, dài 12 cm, rộng 6 cm, bị cắt mất một phần hình vuông có cạnh 3 cm ở một góc (Hình vẽ).
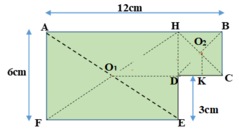
Chọn đáp án đúng
A. Trọng tâm G của bản phẳng nằm trên đoạn O 1 O 2 cách O 1 một đoạn 0,88 cm.
B. Trọng tâm G của bản phẳng nằm trên đoạn AE cách O 1 một đoạn 0,88 cm
C. Trọng tâm G của bản phẳng nằm trên đoạn BD cách O 1 một đoạn 0,55 cm
D. Trọng tâm G của bản phẳng nằm trên đoạn O 1 D cách O 1 một đoạn 0,55 cm.
Chọn A.
Bản phẳng coi như gồm hai bản AHEF và HBCD ghép lại.
Biểu diễn trọng tâm các bản như hình vẽ sau:
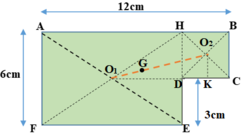
Vì các bản đồng chất, phẳng mỏng đều nên tỉ lệ diện tích bằng tỉ lệ về trọng lượng:
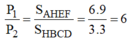
Gọi G là trọng tâm của cả bản phẳng => G phải nằm trền đoạn thẳng O 1 O 2 , trong đó O 1 là trọng tâm của bản AHEF, O 2 là trọng tâm của bản HBCD.
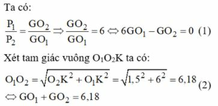
Giải hệ (1) và (2) ta được: O G 1 = 0,88 c m
Vậy trọng tâm G của bản phẳng nằm trên đoạn O 1 O 2 cách O 1 một đoạn 0,88 cm.
Đúng 0
Bình luận (0)
Hãy xác định trọng tâm của một bản phẳng mỏng, đồng chất, hình chữ nhật, dài 12 cm, rộng 6 cm, bị cắt mất một phần hình vuông có cạnh 3 cm ở một góc (Hình vẽ).Chọn đáp án đúng. A. Trọng tâm G của bản phẳng nằm trên đoạn
O
1
O
2
cách
O
1
một đoạn 0,88 cm. B. Trọng tâm G của bản phẳng nằm trên đoạn AE cách
O
1
một...
Đọc tiếp
Hãy xác định trọng tâm của một bản phẳng mỏng, đồng chất, hình chữ nhật, dài 12 cm, rộng 6 cm, bị cắt mất một phần hình vuông có cạnh 3 cm ở một góc (Hình vẽ).
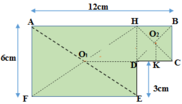
Chọn đáp án đúng.
A. Trọng tâm G của bản phẳng nằm trên đoạn O 1 O 2 cách O 1 một đoạn 0,88 cm.
B. Trọng tâm G của bản phẳng nằm trên đoạn AE cách O 1 một đoạn 0,88 cm.
C. Trọng tâm G của bản phẳng nằm trên đoạn BD cách O 1 một đoạn 0,55 cm.
D. Trọng tâm G của bản phẳng nằm trên đoạn O 1 D cách O 1 một đoạn 0,55 cm.
Chọn A.
Bản phẳng coi như gồm hai bản AHEF và HBCD ghép lại.
Biểu diễn trọng tâm các bản như hình vẽ sau:
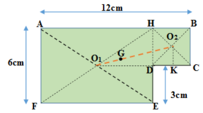
Vì các bản đồng chất, phẳng mỏng đều nên tỉ lệ diện tích bằng tỉ lệ về trọng lượng:
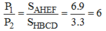
Gọi G là trọng tâm của cả bản phẳng => G phải nằm trền đoạn thẳng O1O2, trong đó O1 là trọng tâm của bản AHEF, O2 là trọng tâm của bản HBCD.
Ta có:
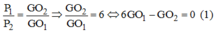
Xét tam giác vuông O1O2K ta có:
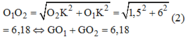
Giải hệ (1) và (2) ta được: GG1 0,88 cm
Vậy trọng tâm G của bản phẳng nằm trên đoạn O1O2 cách O1 một đoạn 0,88 cm.
Đúng 0
Bình luận (0)
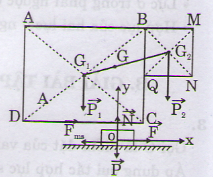
Hãy xác định trọng tâm của một bản phẳng mỏng, đồng chất, hình chữ nhật dài 12cm, rộng 6cm, bị cắt mất một phần hình vuông có cạnh 3cm ở một góc (Hình 19.7)
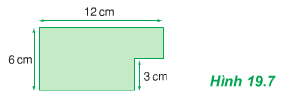
Chia bản mỏng thành hai phần.
ABCD và BMNQ. Trọng tâm của 2 phần này là G1 và G2. Nếu gọi trọng tâm của bản lề G thì G sẽ là điểm đặt của hợp lực của các trọng lực P1 và P2 của hai bản nói trên.
Do trọng lượng của mỗi tấm tỉ lệ với diện tích.
Ta có: =
=
= 6
Khi đó G được xác định như sau:
=
= 6 (1)
Mặt khác ta có: G1G2 = = 6,18 cm
=> GG1 + GG2 = 6,18 (2)
(1)và(2) => GG1 = 0,882 cm
Vậy trọng tâm G nằm trên đường nối G1 và G2; cách G1 một đoạn 0,882cm
Đúng 0
Bình luận (0)
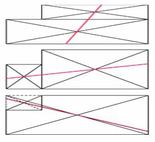
Một hình chữ nhật đã bị cắt đi một hình vuông ở một góc. Chỉ cần một nhát cắt thẳng, bạn hãy chia phần còn lại thành 2 phần có diện tích bằng nhau.

Chỉ cần các bạn biết được tính chất: Mọi đường thẳng đi qua tâm của hình chữ nhật để chia hình chữ nhật thành hai hình có diện tích bằng nhau.
Có thể chia được bằng nhiều cách:
Đúng 0
Bình luận (0)
Một hình chữ nhật đã bị cắt đi một hình vuông ở một góc. Chỉ cần một nhát cắt phẳng, hãy chia phần còn lại thành hai phần có diện tích bằng nhau.
Cho hình chữ nhật ABCD , E là một điểm bất kỳ trên đoạn thẳng OB, trong đó O là tâm hình chữ nhật . Trên tia đối của tia EA lấy điểm F sao cho EF=AE.Qua E kẻ đường thẳng song song với đường chéo AC , đường này cắt cạnh BC tại điểm I và cắt tia DC tại điểm K . Chứng minh
a) CF//DB
b) tứ giác CKFI là hình chữ nhật
Câu 1: Từ một mảnh bìa hình tròn tâm , bán kính , người ta cắt ra một hình gồm 1 hình vuông và 4 hình chữ nhật bằng nhau. Các hình chữ nhật có kích thước là (cm) và (cm). Tìm , để diện tích hình được cắt ra là lớn nhất.











