§3. Phương trình elip
Các câu hỏi tương tự
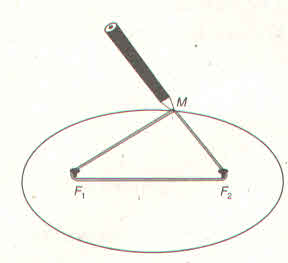
Để cắt một bảng hiệu quảng cáo hình elip có các trục lớn là 80cm và trục nhỏ là 40 cm từ một tấm ván ép hình chữ nhật có kích thước 80cm x 40cm, người ta vẽ một hình elip lên tấm ván như hình 3.19. Hỏi phải ghim hai cái đinh cách các mép tấm ván ép bao nhiêu và lấy vòng dây có độ dài là bao nhiêu? (Bài 4 trang 88 Sách giáo khoa hình học lớp 10)
Để cắt một bảng hiệu quảng cáo hình elip có trục lớn là 80cm và trục nhỏ là 40cm từ một tấm ván ép hình chữ nhật có kích thước 80cm x 40 cm, người ta vẽ hình elip đó lên tấm ván ép như hình 3.19. Hỏi phải ghim hai cái đinh các mép tấm ván ép bao nhiêu và lấy vòng dây có độ dài bao nhiêu ?
Các hành tinh và các sao chổi khi chuyển động xung quanh Mặt Trời có quỹ đạo là một đường Elip trong đó tâm Mặt Trời là một tiêu điểm. Điểm gần Mặt Trời nhất gọi là điểm cận nhật, điểm xa mặt trời nhất gọi là điểm viễn nhật. Trái Đất chuyển động xung quanh Mặt Trời Có quỹ đạo là một Elip có độ dài nữa trục lớn bằng 93.000.000 dặm. Tỉ số khoảng cách giữa điểm cận nhật và điểm viễn nhật đến mặt trời là 59/61. Tính khoảng cách từ Trái Đất đến Mặt Trời khi Trái Đất ở điểm cận nhật.
Đọc tiếp
Các hành tinh và các sao chổi khi chuyển động xung quanh Mặt Trời có quỹ đạo là một đường Elip trong đó tâm Mặt Trời là một tiêu điểm. Điểm gần Mặt Trời nhất gọi là điểm cận nhật, điểm xa mặt trời nhất gọi là điểm viễn nhật. Trái Đất chuyển động xung quanh Mặt Trời Có quỹ đạo là một Elip có độ dài nữa trục lớn bằng 93.000.000 dặm. Tỉ số khoảng cách giữa điểm cận nhật và điểm viễn nhật đến mặt trời là 59/61. Tính khoảng cách từ Trái Đất đến Mặt Trời khi Trái Đất ở điểm cận nhật.
cho elip (e) có pt chính tắc: x^2/9 + y^2/4=1
a) tìm tọa độ đỉnh, tiêu điểm f1, f2, và tâm sai của (e)
b) tìm tọa độ điểm m thuộc (e) thõa mãn mf1 -mf2=2
(f1 là tiêu điểm bên trái của elip)
Cho hai đường tròn C1(F1; R1) và C2(F2; R2). C1 nằm trong C2 và F1 ≠ F2 . Đường tròn (C) thay đổi luôn tiếp xúc ngoài với C1 và tiếp xúc trong với C2.Hãy chứng tỏ rằng tâm M của đường tròn (C) di động trên một elip.
Đọc tiếp
Cho hai đường tròn C1(F1; R1) và C2(F2; R2). C1 nằm trong C2 và F1 ≠ F2 . Đường tròn (C) thay đổi luôn tiếp xúc ngoài với C1 và tiếp xúc trong với C2.Hãy chứng tỏ rằng tâm M của đường tròn (C) di động trên một elip.
Cho elip (E) : \(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\left(0< b< a\right)\). Tính tỉ số \(\dfrac{c}{a}\) trong các trường hợp sau :
a) Trục lớn bằng ba lần trục nhỏ
b) Đỉnh trên trục nhỏ nhìn hai tiêu điểm dưới một góc vuông
c) Khoảng cách giữa đỉnh trên trục nhỏ và đỉnh trên trục lớn bằng tiêu cự
Cho (E): x^2/4 + y^2/1 = 1 và điểm C (2; 0). Tìm tọa độ các điểm A và B thuộc (E) sao cho tam giác ABC là tam giác đều
Cho đường tròn C_1left(F_1;2aright) cố định và một điểm F_2 cố định nằm trong left(C_1right).
Xét đường tròn di động (C) có tâm M. Cho biết (C) luôn đi qua điểm F_2 và (C) luôn tiếp xúc với left(C_1right)
Hãy chứng tỏ M di động trên một elip ?
Đọc tiếp
Cho đường tròn \(C_1\left(F_1;2a\right)\) cố định và một điểm \(F_2\) cố định nằm trong \(\left(C_1\right)\).
Xét đường tròn di động (C) có tâm M. Cho biết (C) luôn đi qua điểm \(F_2\) và (C) luôn tiếp xúc với \(\left(C_1\right)\)
Hãy chứng tỏ M di động trên một elip ?
Một điểm trên trục lớn là điểm ( 3 ; 0 ) và một tiêu điểm là điểm ( -2 ; 0 )