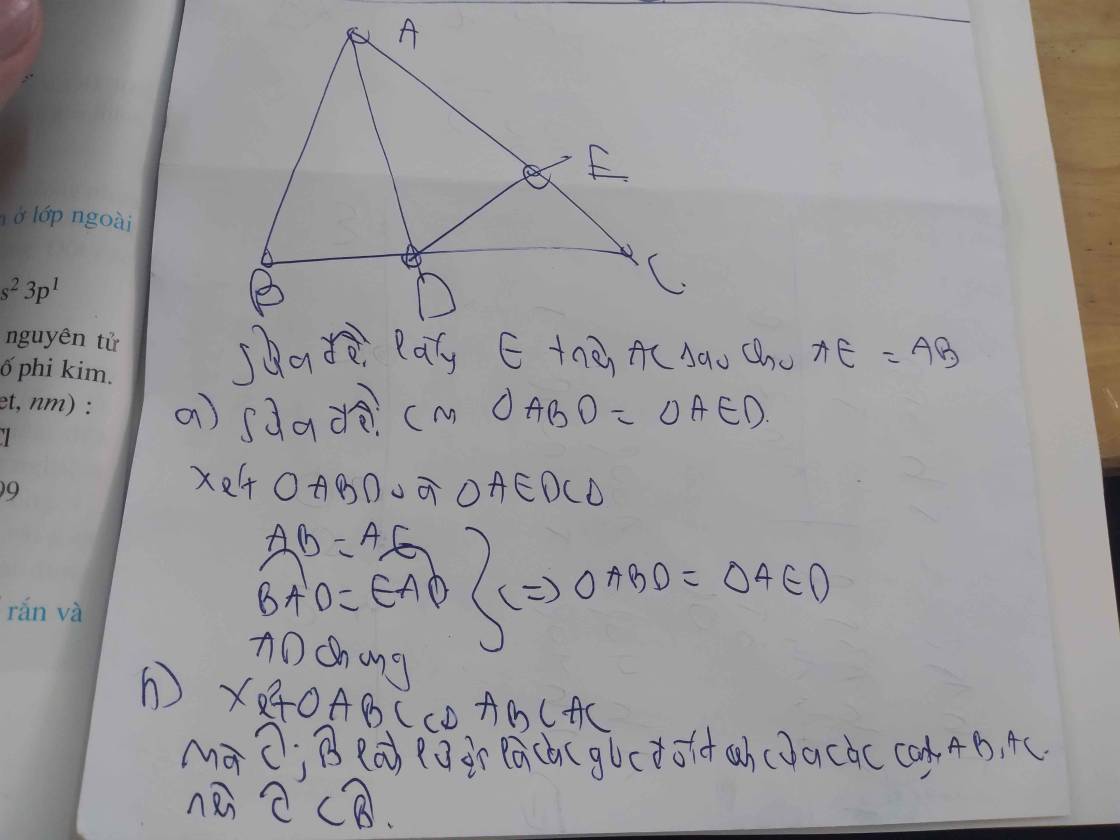
Cho tam giác ABC, D là điểm trên cạnh BC,E là điểm trên đoạn AD. So sánh góc ADC và góc BED; góc ADB và góc AEB

Những câu hỏi liên quan
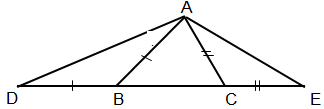
Cho ABC có ( AB < AC) và AD là phân giác của A (DE BC). Gọi E là một điểm bất kỳ thuộc cạnh AD(E khác A;D). Trên cạnh AC lấy điểm F sao cho AF = AB . a) Chứng minh: tam giác ABE = tam giác AFE.
b) So sánh các góc B.và C. So sánh AD và AC biết ADC = 105°
cho \(\Delta\)ABC, D là điểm trên cạnh BC, E là điểm trên đoạn thẳng AD
so sánh góc ADC,BED
'' '' '' ADB , ACB
Cho tam giác ABC có AB < AC, AD là phân giác góc A (D thuộc BC ). Trên cạnh AC lấy điểm E sao cho AE = AB.
a.Cm: CD >BD
b.Cm: so sánh góc ADB và góc ADC
Bài 1 Cho tam giác ABC có AB<AC . AD là phân giác của góc A(d thuộc BC). Trên AC lấy E sao cho AE=AB
a) chứng minh rằng CD>BD
b) so sánh góc ADB và góc ADC
Bài 2 Cho tâm giác ABC có góc A là góc tù. Trên AB lấy điểm D
a) so sánh các đợn thẳng CA, CD, CB
b) trên AC lấy E. so sánh DE và BC
cho tam giác ABC có góc = 90 độ Tia phân giác BD của góc D Trên cạnh BC lấy điểm E sao BE=BA
a)so sánh độ dài các đoạn AD và DE so sánh góc EDC và ABC
b)chứng minh AE vuông góc AD
a: Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔABD=ΔEBD
Suy ra: DA=DE
Đúng 1
Bình luận (0)
a) Vì BD là phân giác của ABC nên ABD = CBD
Xét Δ ABD và Δ EBD có:
BA = BE (gt)
ABD = EBD (cmt)
BD là cạnh chung
Do đó, Δ ABD = Δ EBD (c.g.c)
=> AD = DE (2 cạnh tương ứng) (đpcm)
b) Δ ABD = Δ EBD (câu a) => BAD = BED = 90o (2 góc tương ứng)
=> Δ DEC vuông tại E
Δ ABC vuông tại A có: ABC + C = 90o (1)
Δ CED vuông tại E có: EDC + C = 90o (2)
Từ (1) và (2) => ABC = EDC (đpcm)
c) Gọi giao điểm của AE và BD là H
Xét Δ ABH và Δ EBH có:
AB = BE (gt)
ABH = EBH (câu a)
BH là cạnh chung
Do đó, Δ ABH = Δ EBH (c.g.c)
=> BHA = BHE (2 góc tương ứng)
Mà BHA + BHE = 180o (kề bù) nên BHA = BHE = 90o
=> BH⊥AEBH⊥AE hay BD⊥AE(đpcm)
Đúng 1
Bình luận (0)
Cho góc xAy có tia phân giác là Ad. Trên Ax, Ay lấy lần lượt hai điểm B và D sao cho AB AD. C là một điểm trên Ad sao cho góc ABC tù.a) CMR: tam giác ACB tam giác ACDb) So sánh: ACB và ACD; BC và DCc) Vẽ đường tròn tâm C, bán kính CB, cắt Ax tại điểm E. Hãy chứng tỏ hai tam giác AEC, ADC có hai cặp cạnh và một cặp góc bằng nhau. Với kết quả đó có kết luận ngay hai tam giác AEC, ADC có bằng nhau không? Vì sao?
Đọc tiếp
Cho góc xAy có tia phân giác là Ad. Trên Ax, Ay lấy lần lượt hai điểm B và D sao cho AB= AD. C là một điểm trên Ad sao cho góc ABC tù.
a) CMR: tam giác ACB = tam giác ACD
b) So sánh: ACB và ACD; BC và DC
c) Vẽ đường tròn tâm C, bán kính CB, cắt Ax tại điểm E. Hãy chứng tỏ hai tam giác AEC, ADC có hai cặp cạnh và một cặp góc bằng nhau. Với kết quả đó có kết luận ngay hai tam giác AEC, ADC có bằng nhau không? Vì sao?
1) Cho tam giác ABC có ABAC. Tia phân giác của góc A cắt BC ở D. Trên cạnh AC lấy một điểm E sao cho AE ABa) C/m tam giác ABD tam giác AEDb) C/m AD vuông góc với BEc) Chứng minh góc ADB góc ADC2) Cho tam giác ABC có ABAC, AD là tia phân giác của góc BAC ( D thuộc BC ). Trên cạnh AC lấy một điểm E sao cho AE ABa) C/m tam giác ADB tam giác ADEb) Gọi F là giao điểm của tia AB và tia ED. Chứng minh tam giác BFD tam giác ECDc) So sánh DB và DC
Đọc tiếp
1) Cho tam giác ABC có AB<AC. Tia phân giác của góc A cắt BC ở D. Trên cạnh AC lấy một điểm E sao cho AE = AB
a) C/m tam giác ABD = tam giác AED
b) C/m AD vuông góc với BE
c) Chứng minh góc ADB < góc ADC
2) Cho tam giác ABC có AB<AC, AD là tia phân giác của góc BAC ( D thuộc BC ). Trên cạnh AC lấy một điểm E sao cho AE = AB
a) C/m tam giác ADB = tam giác ADE
b) Gọi F là giao điểm của tia AB và tia ED. Chứng minh tam giác BFD = tam giác ECD
c) So sánh DB và DC
Cho tam giác ABC với AC < AB. Trên tia đối của BC lấy điểm D saoc ho BD = AB. Trên tia đối của tia CB lấy điểm E sao cho CE = AC. Vẽ các đoạn thẳng AD, AE
a) Hãy so sánh góc ADC và góc AEB
b) Hãy so sánh các đoạn AD và AE
a.
b. Xét ΔADE có góc ADE < góc AED (chứng minh ở phần a)
=> AE < AD (Quan hệ giữa góc - cạnh đối diện trong tam giác)
Đúng 0
Bình luận (0)
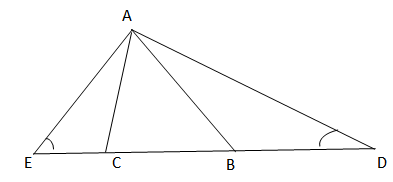
a) So sánh ˆADCADC^ và ˆAECAEC^
Ta có: AC < AB
=> ˆABC<ˆACBABC^<ACB^ (1)
Vì AC = EC => ∆AEC cân tại C
=> ˆAEC<ˆCAEAEC^<CAE^
Mà ˆACB=ˆAEC+ˆEACACB^=AEC^+EAC^ (góc ngoài tại C của ∆AEC)
=> ˆACB=2.ˆAECACB^=2.AEC^ (2)
Chứng minh tương tự : ˆABC=2ˆADCABC^=2ADC^ (3)
Từ (1), (2), (3) => 2ˆAEC=2ˆADC2AEC^=2ADC^ hay ˆAEC=ˆADCAEC^=ADC^
b) ∆AED có:
ˆAED=ˆADEAED^=ADE^ (chứng minh trên) => AD = AE
Đúng 0
Bình luận (0)
a)
b) Xét ΔADE có góc ADE < góc AED (chứng minh ở phần a))
=> AE < AD (Quan hệ giữa góc - cạnh đối diện trong tam giác)
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A có góc A bằng 110 độ. Trên cạnh BC lấy điểm D sao cho góc ADC = 105 độ. Từ C kẻ đt // AD, cắt AB ở E. So sánh các cạnh của tam giác ACE
\(\widehat{EAC}=180^o-\widehat{BAC}=180^o-110^o=70^o\)
Tam giác ABC cân ở A nên \(\widehat{ACB}=\frac{180^o-\widehat{A}}{2}=\frac{180^o-110^o}{2}=35^o\) (1)
CE // AD => \(\widehat{ECD}+\widehat{ADC}=180^o\) (\trong cùng phía)
=> \(\widehat{ECD}=180^o-\widehat{ADC}=180^o-105^o=75^o\) (2)
Ta lại có: \(\widehat{ACE}=\widehat{ECD}-\widehat{ACB}=75^o-35^o=40^o\)
Trong tam giác ACE có \(\widehat{EAC}=70^o;\widehat{ACE}=40^o\)
nên góc còn lại \(\widehat{AEC}=180^o-70^o-40^o=70^o\)
Vậy tam giác ACE cân ở C và ta có:
\(70^o=\widehat{A}=\widehat{E}>\widehat{C}=40^o\)
CA = CE > AE
Đúng 0
Bình luận (0)