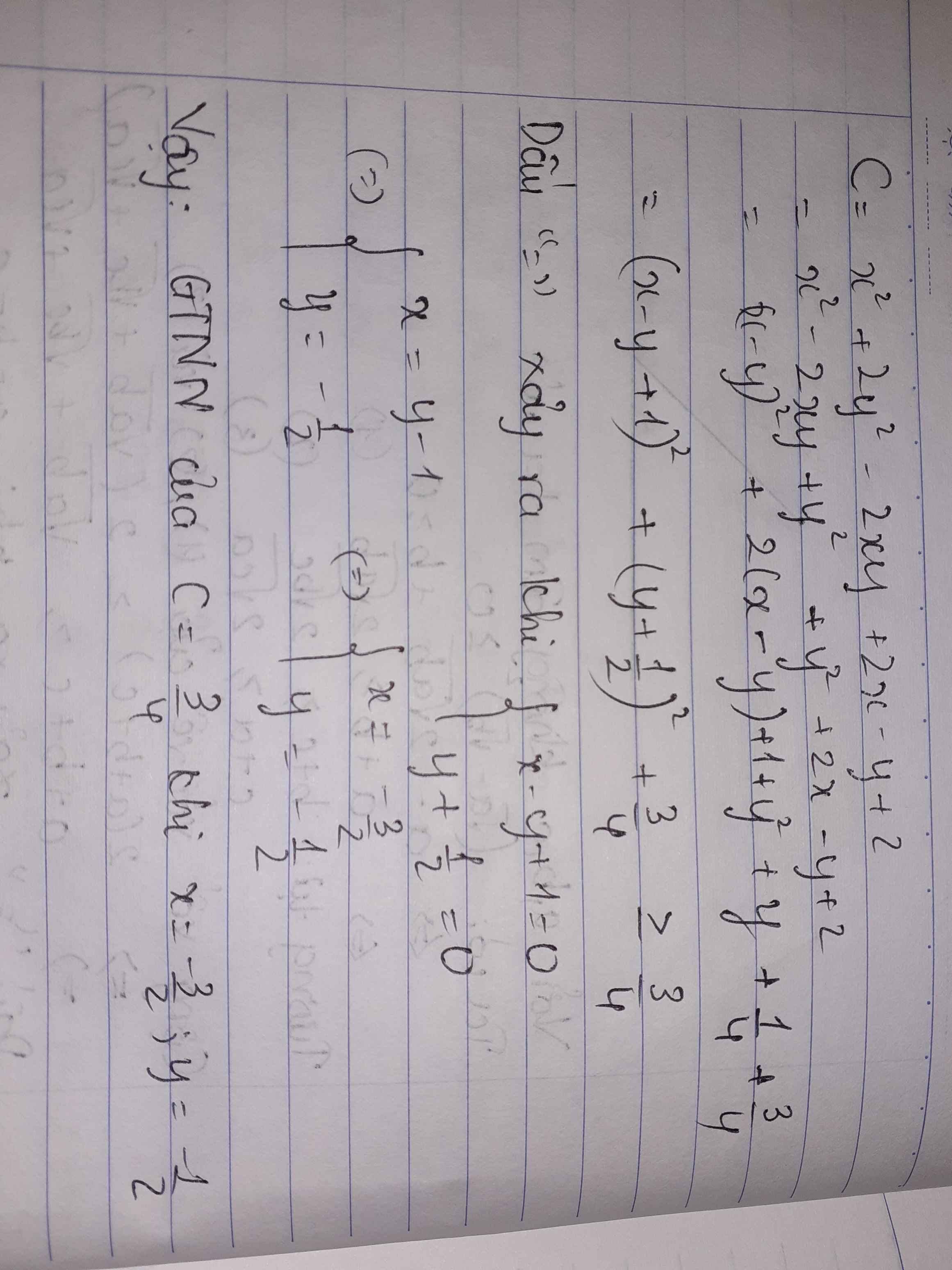1/B=\(-\left(x^2+2y^2+2xy-2y\right)\)

     =\(-\left(x^2+2xy+y^2+y^2-2y+1-1\right)\)

     =\(-\left[\left(x+y\right)^2+\left(y-1\right)^2\right]+1\)<=1

Bmax=1 khi x+y=0 và y-1=0=>x=-1;y=1

2/C=\(x^2+x+\frac{1}{4}+y^2+y+\frac{1}{4}+\frac{1}{2}\)

      =\(\left(x+\frac{1}{2}\right)^2+\left(y+\frac{1}{2}\right)^2+\frac{1}{2}\)>=\(\frac{1}{2}\)

Cmin=\(\frac{1}{2}\)khi \(x+\frac{1}{2}=0\)và \(y+\frac{1}{2}=0\)=>\(x=y=\frac{-1}{2}\)

\(S=\left(x^2+y^2+1+2xy+2x+2y\right)+\left(y^2-4y+4\right)+2021\)

\(S=\left(x+y+1\right)^2+\left(y-2\right)^2+2021\ge2021\)

Dấu "=" xảy ra khi \(\left(x;y\right)=\left(-3;2\right)\)

Ai giúp mik với ạ 😢😭😭😭😭😢😷

\(A=\left(x^2+y^2+36-2xy-12x+12y\right)+5y^2-10y+5+109\)

\(A=\left(x-y-6\right)^2+5\left(y-1\right)^2+109\ge109\)

\(A_{min}=109\) khi \(\left\{{}\begin{matrix}x=7\\y=1\end{matrix}\right.\)

x^2+y^2+2x+2y+2xy+5

bài này rễ quá

giá trị nhỏ nhất của A là 5 nhé

a: A=(x-1)(x-3)(x²-4x+5)

\(=\left(x^2-4x+3\right)\left(x^2-4x+5\right)\)

\(=\left(x^2-4x\right)^2+8\left(x^2-4x\right)+15\)

\(=\left(x^2-4x+4\right)^2-1\)

\(=\left(x-2\right)^4-1>=-1\)

Dấu = xảy ra khi x-2=0

=>x=2

b: \(B=x^2-2xy+2y^2-2y+1\)

\(=x^2-2xy+y^2+y^2-2y+1\)

\(=\left(x-y\right)^2+\left(y-1\right)^2>=0\)

Dấu = xảy ra khi x-y=0 và y-1=0

=>x=y=1

c: \(C=5+\left(1-x\right)\left(x+2\right)\left(x+3\right)\left(x+6\right)\)

\(=-\left(x-1\right)\left(x+6\right)\left(x+2\right)\left(x+3\right)+5\)

\(=-\left(x^2+5x-6\right)\left(x^2+5x+6\right)+5\)

\(=-\left[\left(x^2+5x\right)^2-36\right]+5\)

\(=-\left(x^2+5x\right)^2+36+5\)

\(=-\left(x^2+5x\right)^2+41< =41\)

Dấu = xảy ra khi \(x^2+5x=0\)

=>x(x+5)=0

=>\(\left[{}\begin{matrix}x=0\\x=-5\end{matrix}\right.\)

ta có D=x^2 +2.y^2 -2xy+4x-5y-12

<=>D=(x^2 +y^2 +4 -2xy-4y+4x) +[y^2 -2.y.(1/2) +1/4] -1/4+8

<=>D=(x-y+2)^2 +(y-1/2)^2  +31/4

mà (x-y+2)^2 >= 0 và (y-1/2)^2>=0 nên (x-y+2)^2 +(y-1/2)^2 +31/4 >= 31/4

dấu '=' xảy ra khi :y-1/2=0 và x-y+2=0 <=> y=1/2 và x=-3/2

vậy GTNN của D là 31/4 khi x=-3/2, y=1/2

Bài 1:

a)\(F=x^2+26y^2-10xy+14x-76y+59\)

         \(=\left(x^2-2\cdot x\cdot5y+25y^2\right)+\left(14x-70y\right)+\left(y^2-6x+9\right)+50\)

        \(=[\left(x-5y\right)^2+14\left(x-5y\right)+49]+\left(y-3\right)^2+1\)

          \(=\left(x-5y+7\right)^2+\left(y-3\right)^2+1\ge1\)

 Để Fmin=1 thì y=3;x=8

b)\(H=m^2-4mp+5p^2+10m-22p+28\)

         \(=\left(m^2-2\cdot m\cdot2p+4p^2\right)+\left(10m-20p\right)+\left(p^2-2p+1\right)+27\)

         \(=[\left(m-2p\right)^2+2\cdot\left(m-2p\right)\cdot5+25]+\left(p-1\right)^2+2\)

           \(=\left(m-2p+5\right)^2+\left(p-1\right)^2+2\ge2\)

Để Hmin=2 thì p=1;m=-3

Do A nhỏ nhất 

Suy ra : x^2 = 0, 2y^2 = 0 , 4y = 0 .......( tất cả số hạng bằng 0) 

Suy ra A= 2019

\(A=x^2+2y^2+4y+2xy-4x+2019\)

\(A=\left(x^2+y^2-2^2+2xy-4y-4x\right)+\left(y^2+8y+4^2\right)+2007\)

\(A=\left(x+y-2\right)^2+\left(y+4\right)^2+2007\ge2007\)

Vậy \(Min_A=2007\) khi \(\hept{\begin{cases}x+y-2=0\\y+4=0\end{cases}}\hept{\begin{cases}x+y=2\\y=-4\end{cases}}\hept{\begin{cases}x=6\\y=4\end{cases}}\)