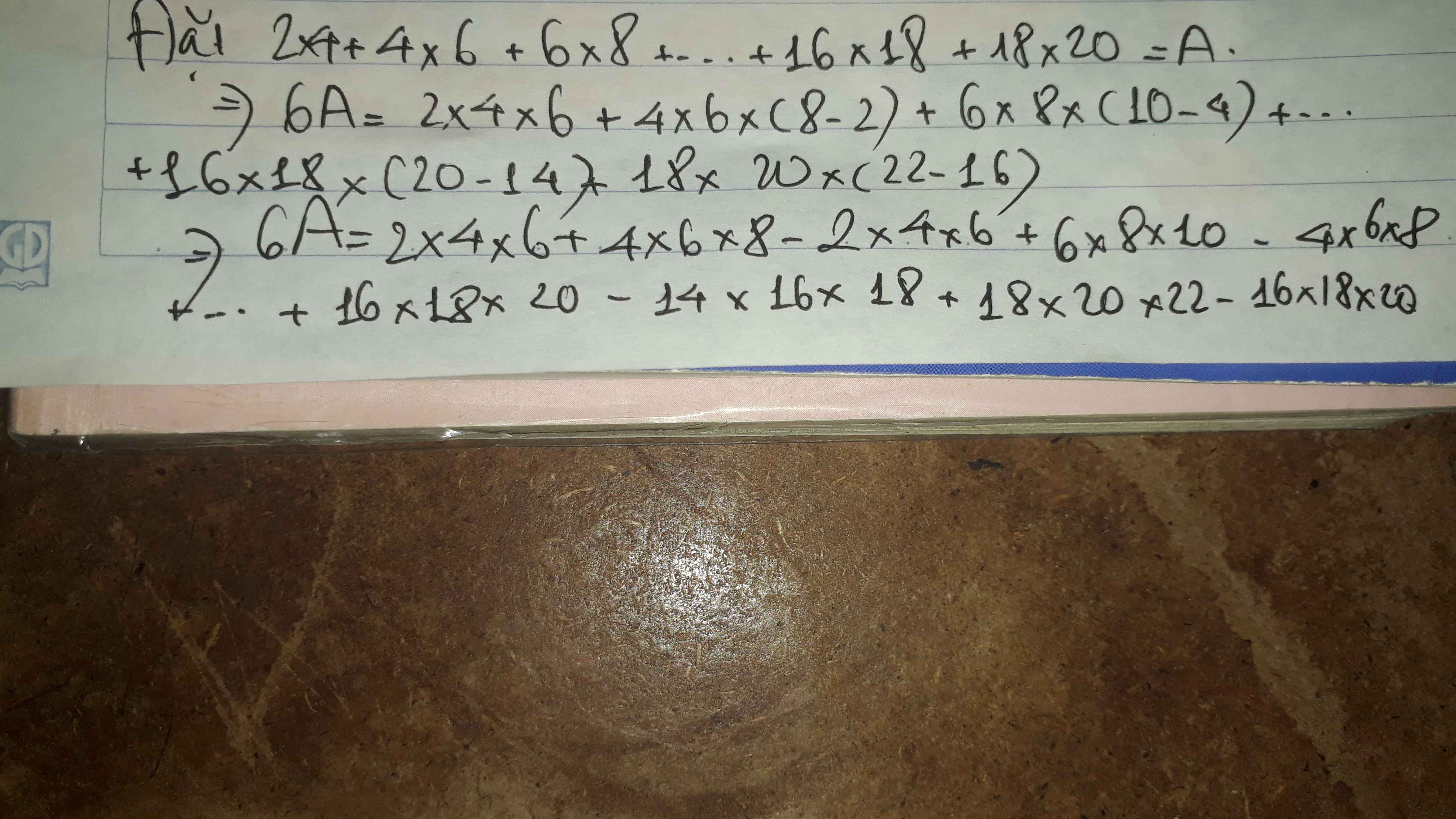S=(2+98)*(4+6)+...+100+100+102

100*10+....+100+100*102
=224400

=1(2+1)+2(3+1)+3(4+1)+...+100(101+1)

=1.2+1+2.3+2+3.4+3+...+100.101+100

=(1.2+2.3+3.4+..+100.101)+(1+2+3+...+100)

=333300+5000

=338300

\(\dfrac{1}{2.4}+\dfrac{1}{4.6}+\dfrac{1}{6.8}+...+\dfrac{1}{40.42}\)

\(=\dfrac{1}{2}\left(\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{8}+...+\dfrac{1}{40}-\dfrac{1}{42}\right)\)

\(=\dfrac{1}{2}.\left(\dfrac{1}{2}-\dfrac{1}{42}\right)\)

\(=\dfrac{1}{2}.\dfrac{10}{21}\)

\(=\dfrac{5}{21}\)

\(#Wendy.Dang\)

\(\dfrac{1}{2\cdot4}+\dfrac{1}{4\cdot6}+\dfrac{1}{6\cdot8}+...+\dfrac{1}{40\cdot42}\)

\(=\dfrac{1}{2}\cdot\left(2\cdot\dfrac{1}{2\cdot4}+\dfrac{1}{4\cdot6}+\dfrac{1}{6\cdot8}+...+\dfrac{1}{40\cdot42}\right)\)

\(=\dfrac{1}{2}\cdot\left(\dfrac{2}{2\cdot4}+\dfrac{2}{4\cdot6}+...+\dfrac{2}{40\cdot42}\right)\)

\(=\dfrac{1}{2}\cdot\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{4}-...+\dfrac{1}{40}-\dfrac{1}{42}\right)\)

\(=\dfrac{1}{2}\cdot\left(1-\dfrac{1}{42}\right)\)

\(=\dfrac{1}{2}\cdot\dfrac{41}{42}\)

\(=\dfrac{41}{84}\)

K = đề bài

   = 2 . ( 2/2.4 + 2/4.6 + 2/6.8 + . . . + 2/2008.2010 )

   = 2 . ( 1 - 1/4 + 1/4 - 1/6 + 1/8 - 1/8 + . . . + 2/2008 - 2/2010 )

   = 2 . ( 1 - 2/2010 )

   = ( phần còn lại bạn tự tính nha )

k cho mình đó, bài này mình làm rồi nên đúng 100% lun, sorry nha mình ngại viết nhiều

a) \(K=\frac{4}{2.4}+\frac{4}{4.6}+\frac{4}{6.8}+...+\frac{4}{2008.2010}\)

\(\Leftrightarrow K=2.\left(\frac{2}{2.4}+\frac{2}{4.6}+...+\frac{2}{2008.2010}\right)\)

\(\Leftrightarrow K=2.\left(1-\frac{1}{2}+\frac{1}{2}-\frac{1}{4}+...+\frac{1}{2008}-\frac{1}{2010}\right)\)

\(\Leftrightarrow K=2.\left(1-\frac{1}{2010}\right)\)

\(\Leftrightarrow K=2.\frac{2009}{2010}=\frac{2009}{1005}\)

b)  F=1/18 + 1/54 + 1/108 +...+ 1/990

=> \(F=\frac{1}{3.6}+\frac{1}{6.9}+\frac{1}{9.12}+...+\frac{1}{30.33}\)

\(\Leftrightarrow F=3.\left(\frac{1}{3.6}+\frac{1}{6.9}+\frac{1}{9.12}+...+\frac{1}{30.33}\right)\)

\(\Leftrightarrow F=\frac{3}{3.6}+\frac{3}{6.9}+\frac{3}{9.12}+...+\frac{3}{30.33}\)

\(\Leftrightarrow F=1-\frac{1}{6}+\frac{1}{6}-\frac{1}{9}+...+\frac{1}{30}-\frac{1}{33}\)

\(\Leftrightarrow F=1-\frac{1}{33}=\frac{32}{33}\)

\(\frac{1}{2.4}+\frac{1}{4.6}+\frac{1}{6.8}+...+\frac{1}{98.100}\)

\(=\frac{1}{2}-\frac{1}{4}+\frac{1}{4}-\frac{1}{6}+\frac{1}{6}-\frac{1}{8}+...+\frac{1}{98}-\frac{1}{100}\)

\(=\frac{1}{2}-\frac{1}{100}\)

\(=\frac{49}{100}\)

Ta có:

\(A=\frac{1}{2.4}+\frac{1}{4.6}+\frac{1}{6.8}+....+\frac{1}{98.100}\)

\(\Rightarrow2A=\frac{2}{2.4}+\frac{2}{4.6}+....+\frac{2}{98.100}\)

\(\Rightarrow2A=\frac{1}{2}-\frac{1}{4}+\frac{1}{4}-\frac{1}{6}+....+\frac{1}{98}-\frac{1}{100}\)

\(\Rightarrow2A=\frac{1}{2}-\frac{1}{100}=\frac{49}{100}\)

\(\Rightarrow A=\frac{49}{100}\div2=\frac{49}{200}\)

Vậy giá trị của biểu thức là \(\frac{49}{200}\)

\(\frac{1}{2.4}+\frac{1}{4.6}+\frac{1}{6.8}+...+\frac{1}{98.100}\)

= \(\frac{1}{2}-\frac{1}{4}+\frac{1}{4}-\frac{1}{6}+\frac{1}{6}-\frac{1}{8}+...+\frac{1}{98}-\frac{1}{100}\)

= \(\frac{1}{2}-\frac{1}{100}\)

= \(\frac{49}{100}\)

Ps: Tham khảo: [Toán nâng cao 5] - Tính nhanh phân số - tth - YouTube

1007/2016

TA có 

4-2/2*4+6-4/4*6+8-6/6*8+...+2016-2014/2014*2016

=1/2-1/4+1/4-1/6+...+1/2014-1/2016

=1/2+1/4-1/4+1/6-1/6+...+1/2014-1/2014-1/2016

=1/2-1/2016

=1007/2016

2/2x4+2/4x6+2/6x8+......................+2/2014x2016

=1/2-`1/4+1/4-1/6+1/6-1/8 +..............................+1/2014-1/2016

=1/2-1/2016

=1007/2016