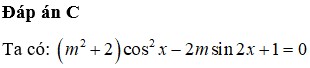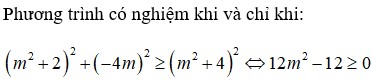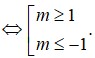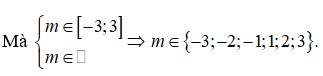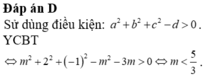Cho phương trình ln2(e.x2)+2m.lnx/e+m2=0. tìm tất cả các giá trị nguyên của tham số m thuộc đoạn [1;6] để phương trình đã cho có hai nghiệm.

Những câu hỏi liên quan
Có tất cả bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-3; 3] để phương trình
(
m
2
+
2
)
c
o
s
2
x
-
2
m
sin
2
x
+
1
0
có nghiệm A. 3 B. 7 C. 6 D. 4
Đọc tiếp
Có tất cả bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-3; 3] để phương trình ( m 2 + 2 ) c o s 2 x - 2 m sin 2 x + 1 = 0 có nghiệm
A. 3
B. 7
C. 6
D. 4
Cho phương trình
m
2
-
3
m
+
2
x
+
m
2
+
4
m
+
5
0
. Tìm tất cả các giá trị thực của tham số m để phương trình đã cho có nghiệm đúng với mọi x thuộc R. A. m −2. B. m −5. C. m 1. D. Không tồn tại.
Đọc tiếp
Cho phương trình m 2 - 3 m + 2 x + m 2 + 4 m + 5 = 0 . Tìm tất cả các giá trị thực của tham số m để phương trình đã cho có nghiệm đúng với mọi x thuộc R.
A. m = −2.
B. m = −5.
C. m = 1.
D. Không tồn tại.
Phương trình đã cho nghiệm đúng với hay phương trình có vô số nghiệm khi
m 2 − 3 m + 2 = 0 − ( m 2 + 4 m + 5 ) = 0 ⇔ m = 1 m = 2 m ∈ ∅ ⇔ m ∈ ∅
Đáp án cần chọn là: D
Đúng 0
Bình luận (0)
Cho phương trình
x
2
– (2m + 1)x +
m
2
+ 1 0, với m là tham số. Tìm tất cả các giá trị của m
∈
ℤ
để phương trình có hai nghiệm phân biệt
x
1
;
x
2
sao cho biểu thức
P
x
1
x...
Đọc tiếp
Cho phương trình x 2 – (2m + 1)x + m 2 + 1 = 0, với m là tham số. Tìm tất cả các giá trị của m ∈ ℤ để phương trình có hai nghiệm phân biệt x 1 ; x 2 sao cho biểu thức P = x 1 x 2 x 1 + x 2 có giá trị là số nguyên
A. m = 1
B. m = 2
C. m = −2
D. m = 0
Cho phương trình x2 - (2m+1)x + m2 +1 = 0 , với m là tham số . Tìm tất cả các giá trị m ∈ Z để phương trình có hai nghiệm phân biệt x1 , x2 sao cho biểu thức \(P=\dfrac{x_1x_2}{x_1+x_2}\)
có giá trị là số nguyên
Đk để pt trên có 2 nghiệm phân biệt x1,x2 : a>0 và denta>0
suy ra denta= (2m+1)^2-4.(m^2+1)>0
suy ra : m>3/4
Ta có P=x1x2/x1+x2=(m^2+1)/(2m+1)
Ta có: P∈Z
⇒4P∈Z
⇒(4m^2+4)/2m+1=(2m-1)+5/2m+1∈Z
⇒2m+1=Ư(5)={−5;−1;1;5}
⇒m={−3;−1;0;2}
Kết hợp đk m>3/4 ta được m=2
Đúng 1
Bình luận (0)
Cho phương trình
m
x
2
+
(
m
2
-
3
)
x
+
m
0
. Tìm tất cả các giá trị của tham số m để phương trình có hai nghiệm
x
1
;
x
2
thỏa mãn
x
1
+
x
2...
Đọc tiếp
Cho phương trình m x 2 + ( m 2 - 3 ) x + m = 0 . Tìm tất cả các giá trị của tham số m để phương trình có hai nghiệm x 1 ; x 2 thỏa mãn x 1 + x 2 = 13 4 . Khi đó tổng bình phương các giá trị tìm được của tham số m bằng:
A. 265 16
B. 16
C. 9 16
D. 73 16
Phương trình có 2 nghiệm x 1 , x 2 thỏa mãn x 1 + x 2 = 13 4
⇔ a ≠ 0 Δ ≥ 0 − b a = 13 4 ⇔ m ≠ 0 m 2 − 3 3 − 4 m 2 ≥ 0 − m 2 − 3 m = 13 4
⇔ m ≠ 0 m 2 − 3 − 2 m m 2 − 3 + 2 m ≥ 0 4 m 2 + 13 m − 12 = 0
⇔ m ≠ 0 m + 1 m − 3 m − 1 m + 3 ≥ 0 m = 3 4 ; m = − 4
⇔ m ≠ 0 m ∈ − ∞ ; − 3 ∪ − 1 ; 1 ∪ 3 ; + ∞ m = 3 4 ; m = − 4 ⇔ m = 3 4 m = − 4
Vậy tổng bình phương các giá trị của m là: 265 16
Đáp án cần chọn là: A
Đúng 0
Bình luận (0)
hehe 1000000% dễễễễ
Tìm tất cả các giá trị thực của tham số m để phương trình 22x-1 + m2 – m = 0 có nghiệm.
A. m < 0
B. 0 < m < 1
C. m < 0; m > 1
D. m > 1
Chọn B.
Phương trình đã cho tương đương : 22x-1 = - m2 + m
Vì 2x - 1 có miền giá trị là R nên 22x-1 có miền giá trị là ![]()
do đó phương trình có nghiệm khi và chỉ khi –m2 + m > 0 hay 0 < m < 1.
Đúng 0
Bình luận (0)
Cho phương trình chứa tham số m:
x
2
+
y
2
+
z
2
-
2
m
x
-
4
y
+
2
z
+
m
2
+
3
m
0
. Tìm tất cả các giá trị thực của tham số m để phương trình đó là phương trình mặt cầu A.
M
ọ
i
m
∈
ℝ
B. ...
Đọc tiếp
Cho phương trình chứa tham số m: x 2 + y 2 + z 2 - 2 m x - 4 y + 2 z + m 2 + 3 m = 0 . Tìm tất cả các giá trị thực của tham số m để phương trình đó là phương trình mặt cầu
A. M ọ i m ∈ ℝ
B. m > 5 3
C. m ≤ 5 3
D. m < 5 3
Cho phương trình
log
3
2
x
+
log
3
2
x
+
1
-
2
m
-
1
0
. Tập tất cả các giá trị của tham số m để phương trình có nghiệm thuộc đoạn
1
;
3
3
là A.
0
≤
m
≤...
Đọc tiếp
Cho phương trình log 3 2 x + log 3 2 x + 1 - 2 m - 1 = 0 . Tập tất cả các giá trị của tham số m để phương trình có nghiệm thuộc đoạn 1 ; 3 3 là
A. 0 ≤ m ≤ 1
B. 0 ≤ m ≤ 2
C. 0 ≤ m ≤ 13 6
D. 1 ≤ m ≤ 2
Điều kiện: x > 0
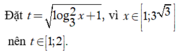
Phương trình trở thành
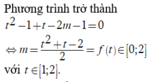
Do đó yêu cầu bài toán ![]()
Chọn B.
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m để phương trình m 2 - 1 x = m - 1 có nghiệm đúng với mọi x thuộc R.
A. m =1.
B. m = ±1.
C. m = −1.
D. m = 0.
Phương trình đã cho nghiệm đúng với ∀ x ∈ R hay phương trình có vô số nghiệm khi m 2 − 1 = 0 m − 1 = 0 ⇔ m = 1
Đáp án cần chọn là: A
Đúng 0
Bình luận (0)