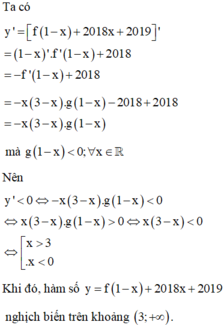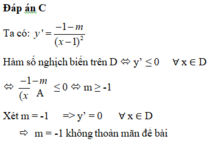Chứng tỏ rằng hàm số y=f(x)=\(\dfrac{x+1}{x-2}\) nghịch biến trong khoảng xác định của nó

Những câu hỏi liên quan
Cho hàm số yf(x) xác định trên
ℝ
và có đồ thị của hàm số f’(x) và các khẳng định sau:(1). Hàm số yf(x) đồng biến trên khoảng
1
;
+
∞
(2). Hàm số yf(x) nghịch biến trên khoảng
-
∞
;
-
2
(3). Hàm số yf(x) nghịch biến trên khoảng
-...
Đọc tiếp
Cho hàm số y=f(x) xác định trên ℝ và có đồ thị của hàm số f’(x) và các khẳng định sau:
(1). Hàm số y=f(x) đồng biến trên khoảng 1 ; + ∞
(2). Hàm số y=f(x) nghịch biến trên khoảng - ∞ ; - 2
(3). Hàm số y=f(x) nghịch biến trên khoảng - 2 ; 1 .
(4). Hàm số y = f x 2 đồng biến trên khoảng - 1 ; 0
(5). Hàm số y = f x 2 nghịch biến trên khoảng (1;2)

Số khẳng định đúng là
A. 4
B. 3
C. 2
D. 5
Chứng tỏ rằng hàm số y= f(x) = x^2 - 4x +3 nghịch biến trong khoảng (- vô cực ; 2) và đồng biến trong khoảng (2: vô cực)
tìm các giá trị của m để hàm số
a) \(y=\dfrac{x+m}{x+1}\) nghịch biến trên từng khoảng xác định
b) \(y=\dfrac{2x-3m}{x-m}\) đồng biến trên từng khoảng xác định
a: TXĐ: D=R\{-1}
\(y'=\dfrac{\left(x+m\right)'\left(x+1\right)-\left(x+1\right)'\left(x+m\right)}{\left(x+1\right)^2}\)
\(=\dfrac{x+1-x-m}{\left(x+1\right)^2}=\dfrac{1-m}{\left(x+1\right)^2}\)
Để hàm số nghịch biến trên từng khoảng xác định thì \(y'< 0\forall x\)
=>\(\dfrac{1-m}{\left(x+1\right)^2}< 0\)
=>1-m<0
=>m>1
b: TXĐ: D=R\{m}
\(y=\dfrac{2x-3m}{x-m}\)
=>\(y'=\dfrac{\left(2x-3m\right)'\left(x-m\right)-\left(2x-3m\right)\left(x-m\right)'}{\left(x-m\right)^2}\)
\(=\dfrac{2\left(x-m\right)-\left(2x-3m\right)}{\left(x-m\right)^2}=\dfrac{2x-2m-2x+3m}{\left(x-m\right)^2}\)
\(=\dfrac{m}{\left(x-m\right)^2}\)
Để hàm số đồng biến trên từng khoảng xác định thì \(y'>0\forall x\)
=>\(\dfrac{m}{\left(x-m\right)^2}>0\)
=>m>0
Đúng 0
Bình luận (0)
Cho hàm số yf(x) xác định trên R và có đạo hàm f‘(x) thỏa mãn f’(x)(1-x)(x+2).g(x) + 2018 trong đó g(x)0, mọi x thuộc R. Hàm số yf(1-x)+2018x+2019 nghịch biến trên khoảng nào?
Đọc tiếp
Cho hàm số y=f(x) xác định trên R và có đạo hàm f‘(x) thỏa mãn f’(x)=(1-x)(x+2).g(x) + 2018 trong đó g(x)<0, mọi x thuộc R. Hàm số y=f(1-x)+2018x+2019 nghịch biến trên khoảng nào?
![]()
![]()
![]()
![]()
Cho hàm số y f(x) xác định trên R và có đạo hàm y f (x) thỏa mãn
f
x
1
−
x
x
+
2
.
g
x
+
2018
trong đó
g
x
0
,
∀
x
∈
ℝ
.
Hàm số
y
f
1
−
x...
Đọc tiếp
Cho hàm số y = f(x) xác định trên R và có đạo hàm y = f '(x) thỏa mãn f ' x = 1 − x x + 2 . g x + 2018 trong đó g x < 0 , ∀ x ∈ ℝ . Hàm số y = f 1 − x + 2018 x + 2019 nghịch biến trên khoảng nào?
A. 1 ; + ∞ .
B. (0;3)
C. − ∞ ; 3 .
D. 3 ; + ∞ .
Cho hàm số y f(x) xác định trên
ℝ
và có đạo hàm f (x) thỏa mãn
f
x
1
-
x
x
+
2
.
g
x
+
2018
trong đó
g
x
0
,
∀
x
∈
ℝ
. Hàm số
y...
Đọc tiếp
Cho hàm số y = f(x) xác định trên ℝ và có đạo hàm f '(x) thỏa mãn f ' x = 1 - x x + 2 . g x + 2018 trong đó g x < 0 , ∀ x ∈ ℝ . Hàm số y = f 1 - x + 2018 x + 2019 nghịch biến trên khoảng nào?
A. 1 ; + ∞
B. 0 ; 3
C. - ∞ ; 3
D. 3 ; + ∞
Đáp án D
Ta có y ' = f 1 - x + 2018 x + 2019 ' = 1 - x ' . f ' 1 - x + 2018 = - f ' 1 - x + 2018
= - x 3 - x . g 1 - x - 2018 + 2018 = - x 3 - x . g 1 - x mà g 1 - x < 0 ; ∀ x ∈ ℝ
Nên y ' < 0 ⇔ - x 3 - x . g 1 - x < 0 ⇔ x 3 - x . g 1 - x > 0 ⇔ x 3 - x < 0 ⇔ [ x > 3 x < 0
Khi đó, hàm số y = f 1 - x + 2018 x + 2019 nghịch biến trên khoảng 3 ; + ∞
Đúng 0
Bình luận (0)
tìm các giá trị của m để hàm số
a) \(y=\dfrac{2m-x}{x-3}\) đồng biến trên từng khoảng xác định
b) \(y=\dfrac{x+3}{x+m}\) nghịch biến trên từng khoảng xác định
a: TXĐ: D=R\{3}
\(y=\dfrac{2m-x}{x-3}\)
=>\(y'=\dfrac{\left(2m-x\right)'\left(x-3\right)-\left(2m-x\right)\left(x-3\right)'}{\left(x-3\right)^2}\)
\(=\dfrac{-\left(x-3\right)-2m+x}{\left(x-3\right)^2}\)
\(=\dfrac{3-2m}{\left(x-3\right)^2}\)
Để hàm số đồng biến trên từng khoảng xác định thì y'>0 với mọi x thỏa mãn ĐKXĐ
=>\(\dfrac{3-2m}{\left(x-3\right)^2}>0\)
=>3-2m>0
=>2m<3
=>\(m< \dfrac{3}{2}\)
b: TXĐ: D=R\{-m}
\(y=\dfrac{x+3}{x+m}\)
=>\(y'=\dfrac{\left(x+3\right)'\left(x+m\right)-\left(x+3\right)\left(x+m\right)'}{\left(x+m\right)^2}\)
\(=\dfrac{x+m-x-3}{\left(x+m\right)^2}=\dfrac{m-3}{\left(x+m\right)^2}\)
Để hàm số nghịch biến trên từng khoảng xác định thì \(y'< 0\forall x\in TXĐ\)
=>\(\dfrac{m-3}{\left(x+m\right)^2}< 0\)
=>m-3<0
=>m<3
Đúng 0
Bình luận (0)
Cho hàm số y f (x) xác định trên R và có đạo hàm f’(x) thỏa f’(x) (1–x)(x+2)g(x)+2018 với g(x) 0,
∀
x
∈
R
. Hàm số y f(1 – x) + 2018x + 2019 nghịch biến trên khoảng nào? A.
1
;
+
∞
B.
0
;...
Đọc tiếp
Cho hàm số y = f (x) xác định trên R và có đạo hàm f’(x) thỏa f’(x) = (1–x)(x+2)g(x)+2018 với g(x) < 0, ∀ x ∈ R . Hàm số y = f(1 – x) + 2018x + 2019 nghịch biến trên khoảng nào?
A. 1 ; + ∞
B. 0 ; 3
C. - ∞ ; 3
D. 3 ; + ∞
Đáp án D
Ta có Đáp án D
Ta có y’ = –f’(1 – x) + 2018 = –[1–(1–x)][(1–x)+2]g(1–x) – 2018 + 2018
= –x(3–x)g(1–x)
Suy ra 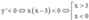 (vì g(1–x) < 0,
∀
x
∈
R
)
(vì g(1–x) < 0,
∀
x
∈
R
)
Vậy hàm số đã cho nghịch biến trên khoảng 3 ; + ∞
Đúng 0
Bình luận (0)
Với giá trị nào của m thì hàm số
y
x
+
m
x
-
1
nghịch biến trên từng khoảng xác định của nó A.
m
-
1
B.
m
≤
-
1
C.
m
-
1
D.
m
≥
-
1
Đọc tiếp
Với giá trị nào của m thì hàm số y = x + m x - 1 nghịch biến trên từng khoảng xác định của nó
A. m < - 1
B. m ≤ - 1
C. m > - 1
D. m ≥ - 1