Bài 24/SGK-Tr.63
Cho các giá trị tương ứng của hai đại lượng x và y
Cho hai đại lượng tỉ lệ nghịch x và y; x 1 , x 2 là hai giá trị của x; y 1 , y 2 là hai giá trị tương ứng của y. Biết x 2 = − 3 ; y 1 = 8 và 4 x 1 + 3 y 2 = 24 . Khi đó x 1 , y 2 =?
A. x 1 = - 6 ; y 2 = 16
B. x 1 = - 6 ; y 2 = - 16
C. x 1 = 16 ; y 2 = - 6
D. x 1 = 6 ; y 2 = 16
Với x và y là hai đại lượng tỉ lệ nghịch nên x 1 y 1 = x 2 y 2 mà x 2 = − 3 ; y 1 = 8 và 4 x 1 + 3 y 2 = 24

Cho hai đại lượng tỉ lệ nghịch x và y; x 1 , x 2 là hai giá trị của x; y 1 , y 2 là hai giá trị tương ứng của y. Biết x 2 = − 3 ; y 1 = 8 và 4 x 1 + 3 y 2 = 24 . Khi đó x 1 , y 2 =?
A. x 1 = - 6 ; y 2 = 16
B. x 1 = - 6 ; y 2 = - 16
C. x 1 = 16 ; y 2 = - 6
D. x 1 = 6 ; y 2 = 16
Với x và y là hai đại lượng tỉ lệ nghịch nên x 1 y 1 = x 2 y 2 mà x 2 = − 3 ; y 1 = 8 và 4 x 1 + 3 y 2 = 24

Bài 1. Cho x và y là hai đại lượng tỉ lệ thuận với nhau. Biết hiệu hai giá trị nào đó của x là 2 và hiệu hai giá trị tương ứng của y là 12. Hỏi đại lượng y và x liên hệ với nhau bởi công thức nào?
x,y tỉ lệ thuận
nên x1/y1=x2/y2
Áp dụng tính chất của DTSBN, ta được:
\(\dfrac{x1}{y1}=\dfrac{x2}{y2}=\dfrac{x1-x2}{y1-y2}=\dfrac{2}{12}=\dfrac{1}{6}\)
=>y=6x
Cho x và y là hai đại lượng tỉ lệ thuận; x1,x2 là hai giá trị khác nhau của x và y1,y2 là các giá trị tương ứng của y. Biết x1-x2=-2 và y1-y2=6. Hãy tìm giá trị của x tương ứng với y=-15?
Lời giải:
Đặt $y=kx$ thì:
$y_1=kx_1$
$y_2=kx_2$
$\Rightarrow y_1-y_2=k(x_1-x_2)$
$\Leftrightarrow 6=k(-2)\Rightarrow k=-3$
Vậy $y=-3x$
Với $y=-15$ thì $-15=-3x$
$\Rightarrow x=5$
Bài 16: Cho x và y là hai đại lượng tỉ lệ nghịch với nhau khi x nhận các giá trị x1 = 3; x2= 2 thì tổng các giá trị tương ứng của y là 15 .
a) Hãy biểu diễn y theo x.
b) Tìm giá trị của x khi y = - 6
a,Vì x và y là 2 đại lượng tỉ lệ nghịch
=> x1/y1 = x2/y2 = x1+x2/y1+y2 = 3+2/15 = 1/3
=>x/y = x1/y1 = 1/3
=>y=3x
b, y=-6
<=> -6=3x
<=> x= -2
Vậy khi y=-6 thì x=-2
Chúc bạn học tốt nha!
cho x và y là hai đại lượng tỉ lệ thuận; x1, x2 là hai giá trị khác nhau của x và y1, y2 là các giá trị tương ứng của y. biết x1 + x2 = 2 và y1 + y2 = 10. Hãy tìm giá trị của y tương ứng với x = -6?
Hai đại lượng x và y tỉ lệ nghịch với nhau. Khi x nhận các giá trị x 1 = 2 , x 2 = 3 thì các giá trị tương ứng y 1 = 36 , y 2 = 24 . Hãy biểu diễn x theo y?
A. x = 72y
B. y = 72x
C. x = 72/y
D. y = 72/x
Hai đại lượng x và y tỉ lệ nghịch với nhau theo hệ số tỉ lệ
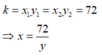
Chọn đáp án C
Các giá trị tương ứng của hai đại lượng \(x\) và \(y\) được cho trong bảng sau. Trong mỗi trường hợp, hãy cho biết đại lượng \(y\) có phải là hàm số của đại lượng \(x\) không? Giải thích.
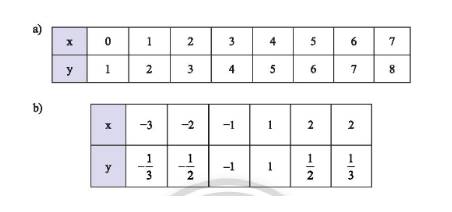
a) Bảng a đại lượng \(y\) là hàm số của đại lượng \(x\) vì với mỗi giá trị của \(x\) ta chỉ nhận được duy nhất một giá trị tương ứng của \(y\).
b) Bảng b đại lượng \(y\) không là hàm số của đại lượng \(x\) vì có những giá trị của \(x\) cho ta hai giá trị \(y\).
Với \(x = 2\) cho ta hai giá trị \(y\) là \(y = \dfrac{1}{2}\) và \(y = \dfrac{1}{3}\).
Cho x và y là hai đại lượng tỉ lệ nghịch và y = a/x. Gọi x 1 , x 2 , x 3 , ....là các giá trị của x và y 1 , y 2 , y 3 , .... là các giá trị tương ứng của y. Ta có:
A. x 1 y 1 = x 2 y 2 = x 3 y 3 = . . . . = 1 a
B. x 1 x 2 = y 2 y 1 = a
C. x 1 y 1 = x 2 y 2 = x 3 y 3 = . . . . = a
D. x 1 y 1 = x 2 y 2 = a
Nếu hai đại lượng y và x tỉ lệ nghịch với nhau theo hệ số tỉ lệ a thì:
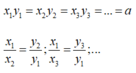
Chọn đáp án C