Bài 32. Tìm các tia phân giác trên hình 91. Hãy chứng minh điều đó.
Những câu hỏi liên quan
Tìm các tia phân giác trên hình 91. Hãy chứng minh điều đó ?
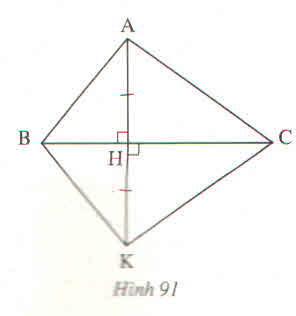
Giải:
∆AHB và ∆KBH có
AH=KH(gt)
\(\widehat{AHB}\)=\(\widehat{KHM}\)
BH cạnh chung .
nên ∆AHB=∆KBH(c.g.c)
suy ra: \(\widehat{ABH}\)=\(\widehat{KBH}\)
Vậy BH là tia phân giác của góc B.
Tương tự ∆AHC =∆KHC(c.g.c)
Suy ra: \(\widehat{ACH}\)=\(\widehat{KCH}\)
Vậy CH là tia phân giác của góc C.
Đúng 0
Bình luận (1)
- Xét ΔAHB và ΔKBH có:
BH cạnh chung
AH = KH
Nên ΔAHB = ΔKBH
Vậy BH là tia phân giác của góc B
- Tương tự ΔAHC = ΔKHC (c.g.c)
Vậy CH là tia phân giác của góc C.
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Cho hình bình hành ABCD. Các tia phân giác của các góc A, B, C, D cắt nhau như trên hình 91. Chứng minh rằng EFGH là hình chữ nhật.
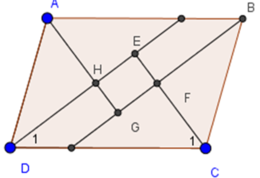
Cho hình bình hành ABCD. Các tia phân giác của các góc A, B, C, D cắt nhau như trên hình 91. Chứng minh rằng EFGH là hình chữ nhật.
Tìm các tia phân giác trên hình 91
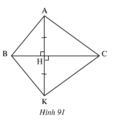
Cho tam giác ABC có M là trung điểm cạnh BC. Trên tia đối của tia MA lấy D sao cho MA=MD. Tìm các tam giác bằng nhau có trên hình vẽ và chứng minh điều đó.
Bài 1: Cho tam giác ABC có M là trung điểm cạnh BC. Trên tia đối của tia MA lấy D sao cho MAMD. Tìm các tam giác bằng nhau có trên hình vẽ và chứng minh điều đó.Bài 2: Cho hai điểm A và B nằm trên đường thẳng xy, trên cùng một nửa mặt phẳng bờ là đường thẳng xy ta kẻ hai đoạn AH và BK cùng vuông góc với xy sao cho AHBK. a) Chỉ ra hai tam giác bằng nhau và chứng minh.b) Chỉ ra các cạnh các góc tương ứng.c) Gọi O là trung điểm HK. So sánh hai tam giác AOH và BOK.
Đọc tiếp
Bài 1: Cho tam giác ABC có M là trung điểm cạnh BC. Trên tia đối của tia MA lấy D sao cho MA=MD. Tìm các tam giác bằng nhau có trên hình vẽ và chứng minh điều đó.
Bài 2: Cho hai điểm A và B nằm trên đường thẳng xy, trên cùng một nửa mặt phẳng bờ là đường thẳng xy ta kẻ hai đoạn AH và BK cùng vuông góc với xy sao cho AH=BK.
a) Chỉ ra hai tam giác bằng nhau và chứng minh.
b) Chỉ ra các cạnh các góc tương ứng.
c) Gọi O là trung điểm HK. So sánh hai tam giác AOH và BOK.
Bài 1: Cho tam giác ABC có M là trung điểm cạnh BC. Trên tia đối của tia MA lấy D sao cho MAMD. Tìm các tam giác bằng nhau có trên hình vẽ và chứng minh điều đó.Bài 2: Cho hai điểm A và B nằm trên đường thẳng xy, trên cùng một nửa mặt phẳng bờ là đường thẳng xy ta kẻ hai đoạn AH và BK cùng vuông góc với xy sao cho AHBK. a) Chỉ ra hai tam giác bằng nhau và chứng minh. b) Chỉ ra các cạnh các góc tương ứng. c) Gọi O là trung điểm HK. So sánh hai tam giác AOH và BOK.Bài 3: Cho ABC, trên tia đối củ...
Đọc tiếp
Bài 1: Cho tam giác ABC có M là trung điểm cạnh BC. Trên tia đối của tia MA lấy D sao cho MA=MD. Tìm các tam giác bằng nhau có trên hình vẽ và chứng minh điều đó.
Bài 2: Cho hai điểm A và B nằm trên đường thẳng xy, trên cùng một nửa mặt phẳng bờ là đường thẳng xy ta kẻ hai đoạn AH và BK cùng vuông góc với xy sao cho AH=BK. a) Chỉ ra hai tam giác bằng nhau và chứng minh. b) Chỉ ra các cạnh các góc tương ứng. c) Gọi O là trung điểm HK. So sánh hai tam giác AOH và BOK.
Bài 3: Cho ABC, trên tia đối của tia AB, xác định điểm D sao cho AD = AB. Trên tia đối của tia AC xác định điểm E sao cho AE = AC. Chứng minh rằng: a) BC // ED b) DBC = BDE
Bài 4: Cho hai đoạn AB và CD cắt nhau tại trung điểm O của mỗi đường. Chứng minh BC // AD.
Bài 5: Cho tam giác ABC có AB = AC. Tia phân giác của góc A cắt BC ở D. Chứng minh: a) DB = DC b) AD BC
Bài 6: Cho tam giác ABC có AB = AC, M là trung điểm của BC, trên tia AM lấy D sao cho AM = MD. Chứng minh: a) ABM = DCM. b) AB // DC. c) AM BC
Bài 7: Qua trung điểm M của đoạn AB vẽ đường thẳng d vuông góc với AB. Trên đường thẳng d lấy điểm K. Chứng minh KM là tia phân giác của góc AKB.
Bài 8: Cho góc xOy có Ot là tia phân giác. Trên hai tia Ox, Oy lần lượt lấy các điểm M, N sao cho OM = ON. Trên tia Ot lấy P bất kì. Chứng minh a) PM = PN. b) Khoảng cách từ P đến hai cạnh của góc xOy bằng nhau.
Bài 9: Cho tam giác ABC có góc A bằng 90 0 . Trên tia đối của tia CA lấy điểm D sao cho CD = CA. Trên tia đối của tia CB lấy điểm E sao cho CE = CB. a) Chứng minh: AB = DE b) Tính số đo góc EDC?
Bài 10: Cho tam giác ABC, M là trung điểm của BC. Trên nửa mặt phẳng bờ là đường thẳng BC không chứa điểm A vẽ tia Cx song song với AB. Trên tia Cx lấy điểm D sao cho CD = AB. Chứng minh: a) MA = MD b) BA điểm A, M, D thẳng hàng.
11: Cho tam giác ABC, M, N là trung điểm của AB và AC. Trên tia đối của tia NM xác định điểm P sao cho NP = MN. Chứng minh: a) CP//AB b) MB = CP c) BC = 2MN
Cho tam giác ABC. Chứng minh rằng giao điểm của hai tia phân giác của hai góc ngoài B1 và C1 (h.32) nằm trên tia phân giác của góc A.
Hình 32
Gọi M là giao điểm của hai tia phân giác của hai góc ngoài B và C của ∆ABC.
Kẻ MH ⊥ AB; MI ⊥ BC; MK ⊥ AC (như hình vẽ)
(H ∈ tia AB, I ∈ BC, K ∈ tia AC)
Theo định lí 1: Điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đó.
Ta có: MH = MI (Vì M thuộc phân giác của góc B ngoài )
MI = MK ( Vì M thuộc phân giác của góc C ngoài )
Suy ra: MH = MK (cùng bằng MI)
Dựa vào định lí 2: Điểm nằm bên trong góc và cách đều hai cạnh của góc thì nằm trên tia phân giác của góc đó.
⇒ M thuộc phân giác của góc BAC (đpcm).
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A (AB AC), đường cao AH, gọi D là trung điểm của AC, lấy điểm E đối xứng với H qua D.a) Chứng minh tứ giác AHCE là hình chữ nhậtb) Qua A kẻ AI song song với HE (I ∈ đường thẳng BC). Chứng minh tứ giác AEHI là hình bình hành.c) Trên tia đối của tia HA lấy điểm K sao cho AH HK. Chứng minh AK là tia phân giác của góc IAC.d) Tìm điều kiện của tam giác ABC để tứ giác CAIK là hình vuông, khi đó tứ giác AHCE là hình gì?
Đọc tiếp
Cho tam giác ABC vuông tại A (AB < AC), đường cao AH, gọi D là trung điểm của AC, lấy điểm E đối xứng với H qua D.
a) Chứng minh tứ giác AHCE là hình chữ nhật
b) Qua A kẻ AI song song với HE (I ∈ đường thẳng BC). Chứng minh tứ giác AEHI là hình bình hành.
c) Trên tia đối của tia HA lấy điểm K sao cho AH = HK. Chứng minh AK là tia phân giác của góc IAC.
d) Tìm điều kiện của tam giác ABC để tứ giác CAIK là hình vuông, khi đó tứ giác AHCE là hình gì?
Có thể giaiar dễ hiểu giùm mk đc ko
Bài 64 (trang 100 SGK Toán 8 Tập 1): Cho hình bình hành ABCD. Các tia phân giác của các góc A, B, C, D cắt nhau như trên hình 91. Chứng minh rằng EFGH là hình chữ nhật.
Bài 64 (trang 100 SGK Toán 8 Tập 1): Cho hình bình hành ABCD. Các tia phân giác của các góc A, B, C, D cắt nhau như trên hình 91. Chứng minh rằng EFGH là hình chữ nhật.
Đúng 0
Bình luận (0)
Theo giả thiết ABCD là hình bình hành nên ta có:
ˆDAB=ˆDCB,ˆADC=ˆABC (1)
Theo định lí tổng các góc của một tứ giác ta có:
ˆDAB+ˆDCB+ˆADC+ˆABC=360o (2)
Từ (1) và (2) ⇒ˆDAB+ˆABC=360o/2=180o
Vì AG là tia phân giác ˆDAB (giả thiết)
⇒⇒ ˆBAG=1/2ˆDAB (tính chất tia phân giác)
Vì BG là tia phân giác ˆABC (giả thiết)
⇒⇒ ˆABG=1/2ˆABC
Do đó: ˆBAG+ˆABG=1/2(ˆDAB+ˆABC)=1/2.1800=90o
Xét ΔAGB= có:
ˆBAG+ˆABG=90o (3)
Áp dụng định lí tổng ba góc trong một tam giác vào tam giác AGBAGB ta có:
ˆBAG+ˆABG+ˆAGB=180o (4)
Từ (3) và (4) ⇒ˆAGB=90o
Chứng minh tương tự ta được: ˆDEC=ˆEHG=90o
Tứ giác EFGH có ba góc vuông nên là hình chữ nhật (dấu hiệu nhận biết hình chữ nhật)
Đúng 0
Bình luận (0)