Các câu hỏi tương tự
cho tam giác ABC. Trên tia đối của tia AB lấy E, trên tia đối của tia AC lấy D. Các tia phân giác của các góc ACB và AED cắt nhau ở S. CMR: góc ESC = ( góc ABD + góc ADE) : 2
( cho em xin hình vẽ nữa ạ )Cho hai đoạn thẳng AB và CD vuông góc với nhau tại trung điểm của mỗi đoạn. Kẻ các đoạn thẳng AC, CB, BD, DA. Tìm các tia phân giác của các góc (khác góc bẹt) trên hình.
BT1: cho xOy có Ot là tia phân giác , C thuộc Om ( C khác O ). Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OAOB.Chứng minh:a,tam giác OAC tam giác OBCb,góc OAC góc OBC và CACBBT2: cho tam giác ABC,kẻ AH vuông góc với BC ( H thuộc BC ). trên tia đối của tia HA , lấy điểm K sao cho HK HA . Nối KB,KC . tìm các cặp tam giác bằng nhau trong hình vẽ ai nhanh mk tick ( vẽ hình luôn nha)
Đọc tiếp
BT1: cho xOy có Ot là tia phân giác , C thuộc Om ( C khác O ). Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA=OB.Chứng minh:
a,tam giác OAC = tam giác OBC
b,góc OAC = góc OBC và CA=CB
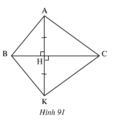
BT2: cho tam giác ABC,kẻ AH vuông góc với BC ( H thuộc BC ). trên tia đối của tia HA , lấy điểm K sao cho HK = HA . Nối KB,KC . tìm các cặp tam giác bằng nhau trong hình vẽ
ai nhanh mk tick ( vẽ hình luôn nha)
cho hình vẽ . Biết O1=O2 ;O3=O4 và hai tia ox ,On đối nhau . Chỉ ra các tia phân giác trên hình bên ; Tính số đo của góc moy
Cho góc vuông xAy , C là 1 điểm thuộc tia phân giác Az của góc xAy . D là hình chiếu của C trên Ax , B là hình chiếu của C trên Ay . Trên các đoạn thẳng AD , AB lần lượt là lá các điểm P,Q sao cho chu vi tam giác APQ bằng AD+AB . Trên tia Dx láy điểm E sao cho DE=QB . Chứng minh :
a, Tam giác CDE = tam giác CPQ
b, Pc là tia phân giác của góc DPQ
c, góc PCQ có số đo = 450
Cho tam giác ABC. Chứng minh rằng giao điểm của hai tia phân giác của hai góc ngoài B1 và C1 nằm trên tia phân giác của góc A
Các bạn vẽ hình giúp mình luôn. Nếu có thể thì ghi GT, KL
cho góc bẹt xOy. Trên cùng một nửa mặt phẳng bờ xy vẽ các tia Om, On sao cho yOm = a độ, yOt = 75 độ trong đó a < 75. Vẽ các tia phân giác On của góc xOm. Tìm giá trị của a để tia Ot là tia phân giác của góc mOn
Cho góc bẹt AOB. Trên cùng nửa mặt phẳng bờ AB vẽ tia OD vuông gíc với OC. Vẽ các tia OE, OF sao cho OA là tia phân giác của COE, OB là tia phân giác của DOF. Chứng tỏ OE vuông góc với OF.
Nếu đc thì vẽ luôn hình giúp mình nha !
Cho tam giác ABC có góc A=120độ . Tia phân giác của góc BAC cắt BC tại D . Tia phân giác của góc ADC cắt AC tại I . Gọi H;K thứ tự là hình chiếu của I . Trên các đường thẳng AB và BC . Chứng minh IH=IK