cho \(8x^2+y^2+\dfrac{1}{4y^2}=4\)
tìm GTLN, GTNN : xy+5
Những câu hỏi liên quan
Cho các số x,y thỏa mãn đẳng thức \(8x^2+y^2+\dfrac{1}{4x^2}=4\). Tìm GTLN, GTNN của biểu thức P = xy
cho 8x^2 +y^2 +1/4x^2=4 .Tìm GTLN,GTNN của A= xy+1/2
\(8x^2+y^2+\frac{1}{4x^2}=4\)
\(A=xy+\frac{1}{2}\)
Đúng 0
Bình luận (0)
Sao không giải luôn đi Thùy Dương chép lại cái đề làm gì ??
Đúng 0
Bình luận (0)
Ta có: \(A=xy+\frac{1}{2}\)
\(\Leftrightarrow xy=\frac{2A-1}{2}=\frac{B}{2}\)
Theo đề bài ta có
\(8x^2+y^2+\frac{1}{4x^2}=4\)
\(\Leftrightarrow32x^4-16x^2+4x^2y^2+1=0\)
\(\Leftrightarrow32x^4-16x^2+B^2+1=0\)
Để pt (theo ẩn x2 ) có nghiệm thi: ∆'\(\ge0\)
\(\Leftrightarrow64-32\left(B^2+1\right)\ge0\)
\(\Leftrightarrow B^2+1\le2\)
\(\Leftrightarrow B^2\le1\)
\(\Leftrightarrow-1\le B\le1\)
\(\Leftrightarrow-1\le2A-1\le1\)
\(\Leftrightarrow0\le A\le1\)
Đúng 0
Bình luận (0)
6 tháng 2 2023 lúc 20:14
1. Cho x,y,z0, x+yle1 và xyz1. Tìm GTLN của biểu thức Pdfrac{1}{1+4x^2}+dfrac{1}{1+4y^2}-sqrt{z+1}
2. Cho x,y,z0, xyzx+y+z. Tìm GTNN của biểu thức Pxy+yz+zx-sqrt{1+x^2}-sqrt{1+y^2}-sqrt{1+z^2} (dùng phương pháp lượng giác hóa)
Đọc tiếp
1. Cho \(x,y,z>0\), \(x+y\le1\) và \(xyz=1\). Tìm GTLN của biểu thức \(P=\dfrac{1}{1+4x^2}+\dfrac{1}{1+4y^2}-\sqrt{z+1}\)
2. Cho \(x,y,z>0\), \(xyz=x+y+z\). Tìm GTNN của biểu thức \(P=xy+yz+zx-\sqrt{1+x^2}-\sqrt{1+y^2}-\sqrt{1+z^2}\) (dùng phương pháp lượng giác hóa)
f(x)(2x-3)^2+(x+4)^2-(3x^2+5x-2) tìm GTNNF2x^2+3y^2-8x+24y-7 tìm GTNNF-5x^2-4y^2+20x-32y+9 tìm GTLNFx^2+y^2-x+y-3 tìm GTNNFF5x^2+y^2-4xy-6x+20 tìm GTNNF-13x^2-4y^2+12xy+20x+37F5x^2+9y^2-12xy+24x-48y+100Cho x+y5 Cho A x^3+y^3-8(x^2+y^2)+xy+2 tính GTLN của ACho x+y+20 Tìm min của B2(x^3+y^3)-15xy+7Cho x+y+20 tìm min của Cx^4+y^4-(x^3+y^3)+2x^2y^2+2xy(x^2+y^2)+13xy
Đọc tiếp
f(x)=(2x-3)^2+(x+4)^2-(3x^2+5x-2) tìm GTNN
F=2x^2+3y^2-8x+24y-7 tìm GTNN
F=-5x^2-4y^2+20x-32y+9 tìm GTLN
F=x^2+y^2-x+y-3 tìm GTNN
F=F=5x^2+y^2-4xy-6x+20 tìm GTNN
F=-13x^2-4y^2+12xy+20x+37
F=5x^2+9y^2-12xy+24x-48y+100
Cho x+y=5 Cho A= x^3+y^3-8(x^2+y^2)+xy+2 tính GTLN của A
Cho x+y+2=0 Tìm min của B=2(x^3+y^3)-15xy+7
Cho x+y+2=0 tìm min của C=x^4+y^4-(x^3+y^3)+2x^2y^2+2xy(x^2+y^2)+13xy
a) cho x,y thỏa mãn 8x^2+y^2+1/4x^2=4
tìm x,y để xy đạt GTNN, GTLN.
b) tìm x,y nguyên 3xy+x+y=17
Tìm GTLN - GTNN của các biểu thức ?* bài 1: Tìm GTNN: a) A (x - 5)² + (x² - 10x)² - 24 b) B (x - 7)² + (x + 5)² - 3 c) C 5x² - 6x +1 d) D 16x^4 + 8x² - 9 e) A (x + 1)(x - 2)(x - 3)(x - 6) f) B (x - 2)(x - 4)(x² - 6x + 6) g) C x^4 - 8x³ + 24x² - 8x + 25 h) D x^4 + 2x³ + 2x² + 2x - 2 i) A x² + 4xy + 4y² - 6x – 12y +4 k) B 10x² + 6xy + 9y² - 12x +15 l) C 5x² - 4xy + 2y² - 8x – 16y +83 m) A (x - 5)^4 + (x - 7)^4 – 10(x - 5)²(x - 7)² + 9 * Bài 2: Tìm GTLN: a) M -7x² + 4x -12 b) N -16x² - 3x +14 c) M...
Đọc tiếp
Tìm GTLN - GTNN của các biểu thức ?
* bài 1: Tìm GTNN:
a) A= (x - 5)² + (x² - 10x)² - 24
b) B= (x - 7)² + (x + 5)² - 3
c) C= 5x² - 6x +1
d) D= 16x^4 + 8x² - 9
e) A= (x + 1)(x - 2)(x - 3)(x - 6)
f) B= (x - 2)(x - 4)(x² - 6x + 6)
g) C= x^4 - 8x³ + 24x² - 8x + 25
h) D= x^4 + 2x³ + 2x² + 2x - 2
i) A= x² + 4xy + 4y² - 6x – 12y +4
k) B= 10x² + 6xy + 9y² - 12x +15
l) C= 5x² - 4xy + 2y² - 8x – 16y +83
m) A= (x - 5)^4 + (x - 7)^4 – 10(x - 5)²(x - 7)² + 9
* Bài 2: Tìm GTLN:
a) M= -7x² + 4x -12
b) N= -16x² - 3x +14
c) M= -x^4 + 4x³ - 7x² + 12x -5
d) N= -(x² + x – 2) (x² +9x+18) +27
* Bài 3:
1) Cho x - 3y = 1. Tìm GTNN của M= x² + 4y²
2) Cho 4x - y = 5. Tìm GTNN của 3x²+2y²
3) Cho a + 2b = 2. Tìm GTNN của a³ + 8b³
* Bài 4: Tìm GTLN và GTNN của các biểu thức:
1) A = (3 - 4x)/(x² + 1)
2) B= (8x + 3)/(4x² + 1)
3) C= (2x+1)/(x²+2)
Cho các số x,y thỏa mãn đẳng thức \(8x^2+y^2+\dfrac{1}{4x^2}=4\). Tìm GTLN, GTNN của biểu thức P = xy
Giúp tí.
\(8x^2+\dfrac{1}{4x^2}+y^2-4=0\)
\(\left(\left(2\sqrt{2}x\right)-\dfrac{\sqrt{2}}{2}.\dfrac{1}{x}\right)^2+y^2=0\)
Cần y=0 => P=0
Đúng 0
Bình luận (0)
31 tháng 12 2021 lúc 20:54
a,Cho x,y,z tm \(\left\{{}\begin{matrix}x^2+y^2+z^2=8\\x+y+z=4\end{matrix}\right.\). CM: \(-\dfrac{8}{3}\le x\le\dfrac{8}{3}\)
b, cho \(x^2+3y^2=1\). Tìm GTLN, GTNN của\(P=x-y\)
c, Cho \(P=\dfrac{x^2-\left(x-4y\right)^2}{x^2+4y^2}\left(x^2+y^2>0\right)\)
Tìm GTLN của P
\(c,P=\dfrac{x^2-x^2+8xy-16y^2}{x^2+4y^2}=\dfrac{8\left(\dfrac{x}{y}\right)-16}{\left(\dfrac{x}{y}\right)^2+4}\)
Đặt \(\dfrac{x}{y}=t\)
\(\Leftrightarrow P=\dfrac{8t-16}{t^2+4}\Leftrightarrow Pt^2+4P=8t-16\\ \Leftrightarrow Pt^2-8t+4P+16=0\)
Với \(P=0\Leftrightarrow t=2\)
Với \(P\ne0\Leftrightarrow\Delta'=16-P\left(4P+16\right)\ge0\)
\(\Leftrightarrow-P^2-4P+4\ge0\Leftrightarrow-2-2\sqrt{2}\le P\le-2+2\sqrt{2}\)
Vậy \(P_{max}=-2+2\sqrt{2}\Leftrightarrow t=\dfrac{4}{P}=\dfrac{4}{-2+2\sqrt{2}}=2+\sqrt{2}\)
\(\Leftrightarrow\dfrac{x}{y}=2+2\sqrt{2}\)
Đúng 3
Bình luận (2)
Bài a hình như sai đề rồi bạn.
Đúng 3
Bình luận (2)
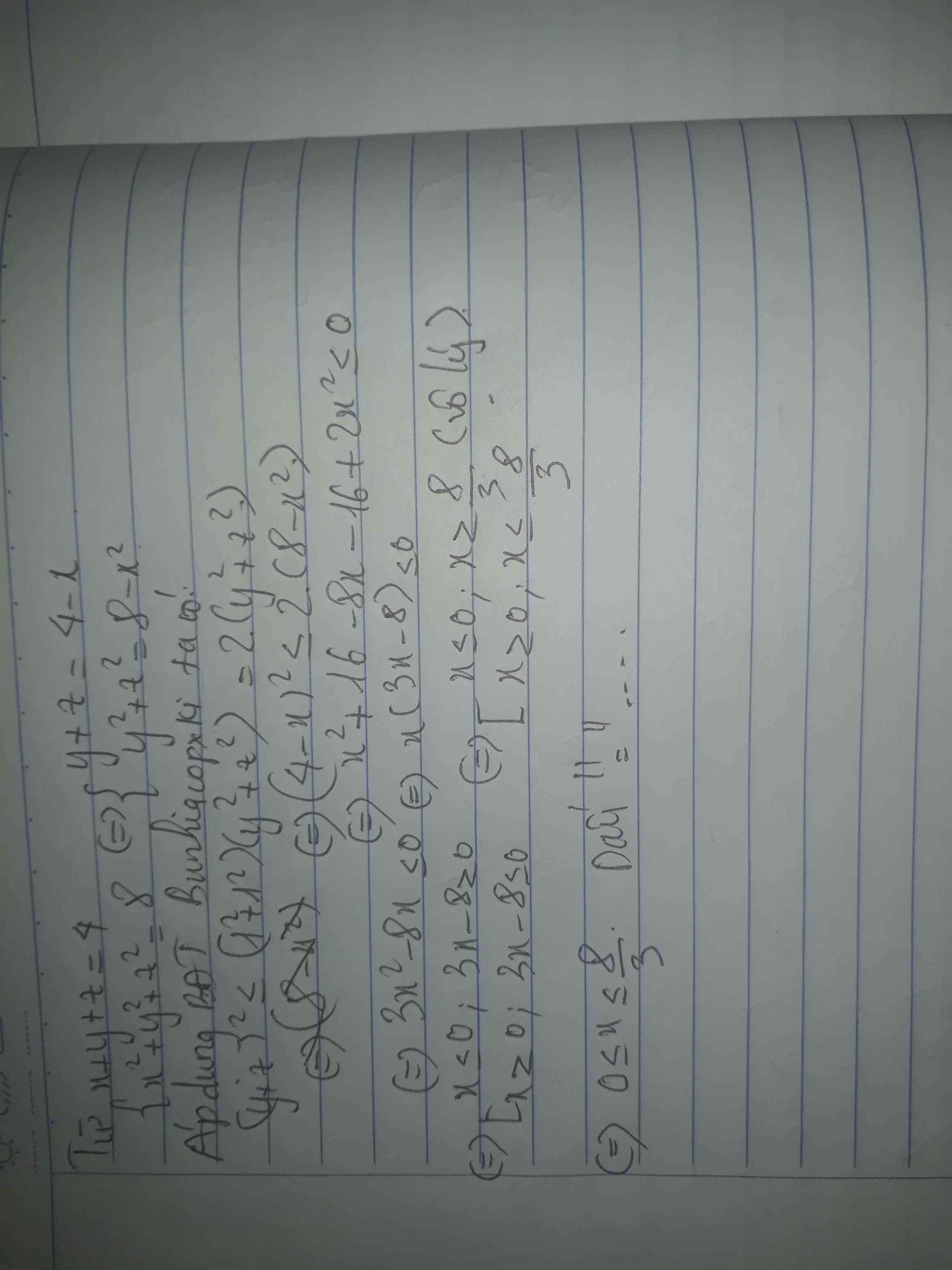
\(a,\text{Đặt }\left\{{}\begin{matrix}S=y+z\\P=yz\end{matrix}\right.\\ HPT\Leftrightarrow\left\{{}\begin{matrix}\left(y+z\right)^2-2yz+x^2=8\\x\left(y+z\right)+yz=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}S^2-2P+x^2=8\\Sx+P=4\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}S^2-2\left(4-Sx\right)+x^2=8\\P=4-Sx\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}S^2+2Sx+x^2-16=0\left(1\right)\\P=4-Sx\end{matrix}\right.\\ \left(1\right)\Leftrightarrow\left(S+x-4\right)\left(S+x+4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}S=-x+4\Rightarrow P=\left(x-2\right)^2\\S=-x-4\Rightarrow P=\left(x+2\right)^2\end{matrix}\right.\)
Mà y,z là nghiệm của hệ nên \(S^2-4P\ge0\Leftrightarrow\left[{}\begin{matrix}\left(4-x\right)^2\ge4\left(x-2\right)^2\\\left(-4-x\right)^2\ge4\left(x+2\right)^2\end{matrix}\right.\Leftrightarrow-\dfrac{8}{3}\le x\le\dfrac{8}{3}\)
Đúng 2
Bình luận (0)
Xem thêm câu trả lời
Bài 1: Tìm min max
x^2 +2xy +7(x+y) +2y^2 +10 = 0
Bài 2 : cho x, y không âm thỏa mãn x+y = 4 tìm GTNN GTLN
p= x^4y+xy^4+x^3+y^3-5(x^2 + y ^2 + 14x^2y^2 -58xy +6
--------- Giúp nha !