Cho hình vẽ. Chứng minh AB//DE và không dùng cách vẽ sng song

Cho tam giác ABC và điểm M nằm bên trong tam giác đó. Vẽ MD song song với AB (D thuộc AC), ME song song với AC (E thuộc AB). Vẽ điểm F đối xứng với M qua đường thẳng DE. Chứng minh : Tứ giác AFDE là hình thang cân.
Cho tam giác ABC cân tại A . A= 50 độ
a, Tính góc B ,C
b, Lấy điểm B thuộc AB , E thuộc AC sao cho AD = AE . Chứng minh DE song song với BC
nói cách làm và vẽ hình nữa nha
Ta có :
tam giác ABC là tam giác cân
=>B=C=(180-A)/2=65
vay B=C=65
ta co AD=AE
=>ADE cân tại a
=>ADE=AED=65(giống như trên)
ta có ADE+EDB=180 (kề bù )
=>65+EDB=180
=>EDB=115
vì EDB+góc B=180(115+65=180)
Và hai góc nằm ở vị trí so le trong
=>DE song song với BC
100% Đúng
Cho hình vẽ bên.
a) Chứng minh AD song song với BC.
b) Trên nửa mặt phẳng có bờ là đường thẳng AB không chứa điểm D, lấy điểm E sao cho = 70°. Chứng minh E, A, D thẳng hàng theo hai cách sau:
Cách 1: Chứng minh = 180°.
Cách 2: Sử dụng tiên đề Ơ-clit.
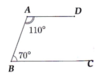
a) Ta có D A B ^ + A B C ^ = 180°.
Mà hai góc ở vị trí trong cùng phía.
Từ đó AD // BC (tính chất hai đường thẳng song song).
b) Cách 1:
E A B ^ + B A D ^ = 70° + 110° = 180°
Cách 2: E A B ^ = A B C ^ = 70°
Mà hai góc ở vị trí so le trong nên AE// BC ( tính chất hai đường thẳng song song)
Lại có AD//BC ( chứng minh ý a)) nên Ad = AE.
Vậy E, A, D thẳng hàng
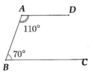
Cho hình vẽ bên.
a) Chứng minh AD song song với BC.
b) Trên nửa mặt phẳng có bờ là đường thẳng AB không chứa điểm D, lấy điểm
E sao cho B A E ^ = 70 ° . Chứng minh E, A,
D thẳng hàng theo hai cách sau:
Cách 1: Chứng minh E A D ^ = 180 ° .
Cách 2: Sử dụng tiên đề Ơ-clit.
Cho tam giác ABC vuông tại A (AB < AC) . M là trung điểm cạnh BC. Vẽ MD vuông góc với AB tại D và ME vuông góc với AC tại E.
a) Chứng minh tứ giác ADME là hình chữ nhật.
b) Chứng minh E là trung điểm của đoạn thẳng AC và tứ giác CMDE là hình bình hành.
c) Vẽ đường cao AH của tam giác ABC. Chứng minh tứ giác MHDE là hình thang cân
d) Qua A vẽ đường thẳng song song với DH cắt DE tại K. Chứng minh HK vuông góc với AC.

a) Xét tứ giác ADME có:
∠(DAE) = ∠(ADM) = ∠(AEM) = 90o
⇒ Tứ giác ADME là hình chữ nhật (có ba góc vuông).
b) Ta có ME // AB ( cùng vuông góc AC)
M là trung điểm của BC (gt)
⇒ E là trung điểm của AC.
Ta có E là trung điểm của AC (cmt)
Chứng minh tương tự ta có D là trung điểm của AB
Do đó DE là đường trung bình của ΔABC
⇒ DE // BC và DE = BC/2 hay DE // MC và DE = MC
⇒ Tứ giác CMDE là hình bình hành.
c) Ta có DE // HM (cmt) ⇒ MHDE là hình thang (1)
Lại có HE = AC/2 (tính chất đường trung tuyến của tam giác vuông AHC)
DM = AC/2 (DM là đường trung bình của ΔABC) ⇒ HE = DM (2)
Từ (1) và (2) ⇒ MHDE là hình thang cân.
d) Gọi I là giao điểm của AH và DE. Xét ΔAHB có D là trung điểm của AB, DI // BH (cmt) ⇒ I là trung điểm của AH
Xét ΔDIH và ΔKIA có
IH = IA
∠DIH = ∠AIK (đối đỉnh),
∠H1 = ∠A1(so le trong)
ΔDIH = ΔKIA (g.c.g)
⇒ ID = IK
Tứ giác ADHK có ID = IK, IA = IH (cmt) ⇒ DHK là hình bình hành
⇒ HK // DA mà DA ⊥ AC ⇒ HK ⊥ AC
Choa tam giác ABC cân tại A . A= 50 độ
a, Tính góc B ,C
b, Lấy điểm B thuộc AB , E thuộc AC sao cho AD = AE . Chứng minh DE song song với BC
nói cách làm và vẽ hình nữa nha
cho tam giác ABC vuông tại A, vẽ tian phân giác BD của góc ABC ( D thuộc A ), Trên BC lấy điểm E sao cho BE = AB, nối D với E
a) chứng minh tam giác ABD = tam giác EBD
b) chứng minh góc BED là góc vuông
c) Vẽ AH vuông góc với BC ( H thuộc BC ). Chúng minh góc BAH = góc ACH và AH song song với DE
d) Chúng minh DB là đường trung trực của AE
không cần vẽ hình nha
a) xét ▲ABD VÀ▲ EBD có
BD là cạnh chung
góc ABD= góc DBE
AB= BE
nên Δ ABD=Δ EBD (c.g.c)
b) vì Δ ABD=Δ EBD (cmt)
→ góc BED= góc BAC (2 góc tương ứng)
c) ta có:
AH VUÔNG VỚI BC
→ góc AHE = 90o (1)
góc bed = 90o (cmt) (2)
từ (1) và (2) suy ra DE song song với AH (2 đường thẳng cùng vuông góc với 1 đường thẳng)
Cho tam giác ABC cân tại A. Trên cạnh AB lấy điểm D, trên tia đối của tia CE lấy E sao cho BD=CE, gọi I là gao điểm của DE và BC . Qua E vẽ đường thẳng song song AB cắt tại F
a, Chứng minh tam giác BDE=tam giác FEI
b,Chứng minh I là trung điểm của DE
Vẽ hình hộ mình với nha CẢM ƠN RẤT NHIỀU
câu 12 cho tam giác ABC điểm D thuộc cạnh BC.Từ điểm D vẽ DE song song với AD sao cho E thuộc cạnh AC,vẽ DF//AC sao cho điểm F thuộc AB chứng minh tứ giác AEDF là hình bình hành.
Xét tứ giác AEDF có
AE//DF
AF//DE
Do đó: AEDF là hình bình hành