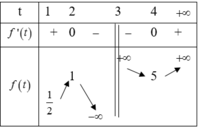
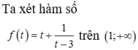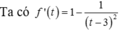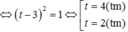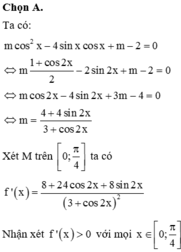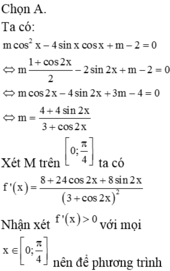Có bao nhiêu số nguyên m để phương trình 4x - m.2x+1 + 9 = 0 có đúng một nghiệm thuộc khoảng (0;2)

Những câu hỏi liên quan
1.Cho phương trình x2 +4x-m=0(1).Tìm tất cả các giá trị của tham số m để phương trinh (1) có đúng 1 nghiệm thuộc khoảng (-3,1)
2.Có bao nhiêu giá trị m nguyên trong nửa khoảng (0;2019] để phương trình |x2 -4|x|-5|-m có hai nghiệm phân biệt
Xét phương trình hoành độ giao điểm\(x^2\)+4x-m=0 <=> x^2+4x=m, đây là kết hợp của 2 hàm số (P):y=\(x^2\)+4x và (d):y=m.
Khi vẽ đồ thị ta thấy parabol đồng biến trên khoảng (-2;+∞)=> Điểm giao giữa parabol và đồ thị y=m là điểm duy nhất thỏa mãn phương trình có duy nhất 1 nghiệm thuộc khoảng (-3;1).Vậy để phương trình có 1 nghiệm duy nhất <=> delta=0 <=>16+4m=0<=>m=-4.
mình trình bày hơi dài mong bạn thông cảm 
Đúng 0
Bình luận (0)
Số giá trị nguyên m thuộc đoạn [-2019; 2019] để phương trình
4
x
-
(
m
-
3
)
.
2
x
+
3
m
+
1
0
có đúng một nghiệm lớn hơn 0 là: A. 2021 B. 2022 C. 2019 D. 2020
Đọc tiếp
Số giá trị nguyên m thuộc đoạn [-2019; 2019] để phương trình
4 x - ( m - 3 ) . 2 x + 3 m + 1 = 0
có đúng một nghiệm lớn hơn 0 là:
A. 2021
B. 2022
C. 2019
D. 2020
Có bao nhiêu giá trị nguyên của m trong khoảng
−
2019
;
2019
để phương trình:
2
x
2
+
2
x
2
−
4
m
−
3
x...
Đọc tiếp
Có bao nhiêu giá trị nguyên của m trong khoảng − 2019 ; 2019 để phương trình:
2 x 2 + 2 x 2 − 4 m − 3 x 2 + 2 x + 1 − 2 m = 0 có đúng 1 nghiệm thuộc − 3 ; 0
A. 2018
B. 4036
C. 4038
D. 4034
Ta có: Δ = 4 m − 3 2 − 4.2. 1 − 2 m = 4 m − 1 2
2 x 2 + 2 x 2 − 4 m − 3 x 2 + 2 x + 1 − 2 m = 0 ⇔ x 2 + 2 x = 1 2 ( 1 ) x 2 + 2 x = 2 m − 1 ( 2 )
( 1 ) ⇔ x 2 + 2 x − 1 2 = 0 ⇔ x = − 2 + 6 2 ∉ − 3 ; 0 x = − 2 − 6 2 ∈ − 3 ; 0
2 ⇔ x + 1 2 = 2 m . Phương trình đã cho có đúng 1 nghiệm thuộc đoạn - 3 ; 0 khi và chỉ khi phương trình (2) có nghiệm nhưng không thuộc đoạn - 3 ; 0 hoặc vô nghiệm.
Xét (2), nếu m < 0 thì (2) vô nghiệm (thỏa mãn yêu cầu).
+) Nếu m = 0 thì (2) có nghiệm duy nhất x = - 1 ∈ - 3 ; 0 (không thỏa yêu cầu).
+) Nếu m > 0 thì (2) có hai nghiệm phân biệt x 1 = − 1 − 2 m < − 1 + 2 m = x 2 nên (2) có hai nghiệm không thuộc - 3 ; 0 nếu
− 1 − 2 m < − 3 − 1 + 2 m > 0 ⇔ m > 2 m > 1 2 ⇔ m > 2
Vậy m < 0 m > 2
Mà m ∈ - 2019 ; 2019 và m ∈ Z nên m ∈ - 2018 ; - 2017 ; . . . ; - 1 ; 3 ; 4 ; . . . ; 2018
Số các giá trị của m thỏa mãn bài toán là 2018 + 2016 = 4034.
Đáp án cần chọn là: D
Đúng 0
Bình luận (0)
Có bao nhiêu giá trị nguyên của tham số m để phương trình 4cos^3 x - cos 2x + (m-3)cos x - 1 = 0 có đúng 4 nghiệm khác nhau thuộc khoảng (-π/2; π/2)
Xem chi tiết
Cho phương trình
tan
x
+
1
3
sin
x
+
2
cos
m
sin
x
+
3
cos
x
. Có bao nhiêu giá trị nguyên của tham số
m
∈...
Đọc tiếp
Cho phương trình
tan x + 1 3 sin x + 2 cos = m sin x + 3 cos x .
Có bao nhiêu giá trị nguyên của tham số m ∈ 0 ; 2019 để phương trình có đúng một nghiệm thuộc khoảng 0 ; π 2
A. 2017
B. 2018
C. 2019
D. 2020
Có bao nhiêu giá trị nguyên của tham số m để phương trình:
4
x
-
(
m
+
3
)
.
2
x
+
1
+
m
+
9
0
có hai nghiệm dương phân biệt A.3 B.4 C.5 D. Vô số
Đọc tiếp
Có bao nhiêu giá trị nguyên của tham số m để phương trình: 4 x - ( m + 3 ) . 2 x + 1 + m + 9 = 0 có hai nghiệm dương phân biệt
A.3
B.4
C.5
D. Vô số
Có bao nhiêu giá trị nguyên của tham số m để phương trình
4
cos
3
x
-
cos
2
x
+
m
-
3
cos
x
-
1
0
có đúng bốn nghiệm khác nhau thuộc khoảng
-
π
2
;...
Đọc tiếp
Có bao nhiêu giá trị nguyên của tham số m để phương trình 4 cos 3 x - cos 2 x + m - 3 cos x - 1 = 0 có đúng bốn nghiệm khác nhau thuộc khoảng - π 2 ; π 2
A. 2
B. 3
C. 0
D. 1
Cho phương trình
m
c
o
s
2
x
-
4
s
i
n
x
c
o
s
x
+
m
-
2
0
. Có bao nhiêu giá trị nguyên của m để phương trình có đúng một nghiệm thuộc
0
;
π...
Đọc tiếp
Cho phương trình m c o s 2 x - 4 s i n x c o s x + m - 2 = 0 . Có bao nhiêu giá trị nguyên của m để phương trình có đúng một nghiệm thuộc 0 ; π 4
A. 2
B. 3
C. 1
D. 0
Cho phương trình
m
cos
2
x
-
4
sin
x
cos
x
+
m
-
2
0
. Có bao nhiêu giá trị nguyên của m để phương trình có đúng một nghiệm thuộc
0
;
π
4
A. 2 B. 3 C. 1 D. 0
Đọc tiếp
Cho phương trình m cos 2 x - 4 sin x cos x + m - 2 = 0 . Có bao nhiêu giá trị nguyên của m để phương trình có đúng một nghiệm thuộc 0 ; π 4
A. 2
B. 3
C. 1
D. 0