Lời giải:

a. Vì $ABCD$ là hình bình hành nên $AB=CD$

$\Rightarrow \frac{1}{2}AB=\frac{1}{2}CD$
$\Rightarrow AF=CE(1)$

Mặt khác: $AB\parallel CD\Rightarrow AF\parallel CE(2)$

Từ $(1); (2)\Rightarrow AECF$ là hình bình hành.

b. 

B, E,F thẳng hàng??? Bạn xem lại đề.

Do E là điểm bất kì trên AB, mà E đối xứng với F qua O => F nằm trên DC⇒ D,F,C thẳng hàng

Do E là điểm bất kì trên AB, mà E đx vs F qua O => F nằm trên DC =>D,F,C thẳng hàng

a) Ta chứng minh A N = C M A N ∥ C M ⇒ A M C N  là hình bình hành.

Vì O là giao điểm của AC và BD, ABCD là hình chữ nhật nên O là trung điểm AC

Do ANCM là hình bình hành có AC và MN là hai đường chéo

⇒  O là trung điểm MN

b. Ta có: EM//AC nên E M D ^ = A C D ^ (2 góc so le trong)

NF//AC nên B N F ^ = B A C ^  (2 góc so le trong)

Mà A C D ^ = B A C ^  (vì AB//DC, tính chất hình chữ nhật)

⇒ E M D ^ = B N F ^

Từ đó chứng minh được  ∆ E D M   =   ∆ F B N   ( g . c . g )

⇒ E M = F N

Lại có EM//FN (vì cùng song song với AC)

Nên tứ giác ENFM là hình bình hành

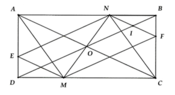
c) Tứ giác ANCM là hình thoi Û AC ^ MN tại O Þ M, N lần lượt là giao điểm của đường thẳng đi qua O, vuông góc AC và cắt CD, AB.

Khi đó M và N là trung điểm của CD và AB.

d) Ta chứng minh được DBOC cân tại O ⇒ O C B ^ = O B C ^   v à   N F B ^ = O C F ^  (đv) Þ DBFI cân tại I Þ IB = IF  (1)

Ta lại chứng minh được DNIB cân tại I Þ IN = IB  (2)

Từ (1) và (2) Þ I là trung điểm của NF.

a Xét tứ giác DEBF có

BE//DF

BE=FD

Do đó; DEBF là hình bình hành

=>DB cắt EF tại trung điểm của mỗi đường(1)

b: Vì ABCD là hình bình hành

nên AC cắt BD tại trung điểm của mõi đường(2)

Từ (1), (2) suy ra AC,BD,EF đồng quy

=>E,O,F thẳng hàng