a, Diện tích tam giác ABC là :

          S ABC^2 = (4+5+8)/2 . [(4+5+8)/2-4] . [(4+5+8)/2-5] . [(4+5+8)/2-6] 

                        = 8,5 . 4,5 . 3,5 . 0,5 = 669,375 ( công thức hê-rông rùi bình phương 2 vế lên )

=> S ABC = 25,87228247 (cm²)

Tk mk nha

k tao ko tao đấm đấy

Đặt câu hỏi gì mà NGU , ĐẦN thế bn

Có phải ở lớp bn có SƯ PHỤ tên là P..... đúng ko
 

Phúc ạ, chắt chê cụ ngu vậy chắt làm đi, ko mai đến lớp cụ sẽ xử đẹp!

a: Xét ΔCAB có \(cosC=\dfrac{CA^2+CB^2-AB^2}{2\cdot CA\cdot CB}\)

=>\(\dfrac{2^2+3-AB^2}{2\cdot2\cdot\sqrt{3}}=cos30=\dfrac{\sqrt{3}}{2}\)

=>\(7-AB^2=4\sqrt{3}\cdot\dfrac{\sqrt{3}}{2}=2\cdot3=6\)

=>AB=1

b: Xét ΔABC có \(AB^2+BC^2=CA^2\)

nên ΔABC vuông tại B

=>\(S_{BAC}=\dfrac{1}{2}\cdot BA\cdot BC=\dfrac{1}{2}\cdot1\cdot\sqrt{3}=\dfrac{\sqrt{3}}{2}\)

Độ dài đường trung tuyến kẻ từ A là:

\(m_A=\sqrt{\dfrac{b^2+c^2}{2}-\dfrac{a^2}{4}}=\sqrt{\dfrac{4+1}{2}-\dfrac{3}{4}}=\dfrac{\sqrt{7}}{2}\)

câu c bài 1 là tích diện tích của tam giác AHM nhá'

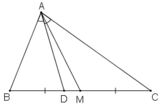
a) Ta có: 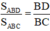 (do hai tam giác có chung chiều cao từ đỉnh A)

ΔABC có AD là phân giác

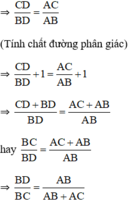
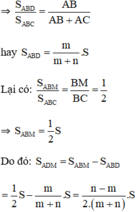
b) Với n = 7; m = 3, thay vào kết quả phần a ta có:

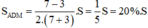
Vậy diện tích tam giác ADM chiếm 20% diện tích tam giác ABC.

AM = 3,125 , AD =15\(\sqrt{2}\): 7

a) Áp dụng hệ thức lượng trong tam giác vuông ABC, ta có:
AH^2=BH.HCAH2=BH.HC\Leftrightarrow HC=\dfrac{AH^2}{HB}=2,25cm⇔HC=HBAH2​=2,25cm.
$BC=BH+HC=4+2,25=6,25cm$.
AM=\dfrac{BC}{2}=3,125cmAM=2BC​=3,125cm.
b) Áp dụng định lý Pi-ta-go ta có:
AB=\sqrt{AH^2+BH^2}=5cmAB=AH2+BH2​=5cm.
 AC=\sqrt{BC^2-AB^2}=\sqrt{6,25^2-5^2}=3,75cmAC=BC2−AB2​=6,252−52​=3,75cm.
Theo tính chất tia phân giác của một góc:\dfrac{BD}{DC}=\dfrac{AB}{AC}=\dfrac{5}{3,75}=\dfrac{4}{3}DCBD​=ACAB​=3,755​=34​.

Gọi E, F là chân đường vuông góc hạ từ D xuống AC và AB. Ta thấy ngay FDEA là hình vuông nội tiếp tam giác vuông ABC.

Từ đó ta có \dfrac{DE}{AB}=\dfrac{DC}{BC}=\dfrac{3}{7}\Rightarrow DE=\dfrac{3}{7}.5=\dfrac{15}{7}\left(cm\right)ABDE​=BCDC​=73​⇒DE=73​.5=715​(cm)

\Rightarrow AD=\dfrac{15\sqrt{2}}{7}\left(cm\right)⇒AD=7152​​(cm).

a) Áp dụng hệ thức lượng trong tam giác vuông ABC, ta có:
AH^2=BH.HCAH2=BH.HC\Leftrightarrow HC=\dfrac{AH^2}{HB}=2,25cm⇔HC=HBAH2​=2,25cm.
$BC=BH+HC=4+2,25=6,25cm$.
AM=\dfrac{BC}{2}=3,125cmAM=2BC​=3,125cm.
b) Áp dụng định lý Pi-ta-go ta có:
AB=\sqrt{AH^2+BH^2}=5cmAB=AH2+BH2​=5cm.
 AC=\sqrt{BC^2-AB^2}=\sqrt{6,25^2-5^2}=3,75cmAC=BC2−AB2​=6,252−52​=3,75cm.
Theo tính chất tia phân giác của một góc:\dfrac{BD}{DC}=\dfrac{AB}{AC}=\dfrac{5}{3,75}=\dfrac{4}{3}DCBD​=ACAB​=3,755​=34​.

Gọi E, F là chân đường vuông góc hạ từ D xuống AC và AB. Ta thấy ngay FDEA là hình vuông nội tiếp tam giác vuông ABC.

Từ đó ta có \dfrac{DE}{AB}=\dfrac{DC}{BC}=\dfrac{3}{7}\Rightarrow DE=\dfrac{3}{7}.5=\dfrac{15}{7}\left(cm\right)ABDE​=BCDC​=73​⇒DE=73​.5=715​(cm)

\Rightarrow AD=\dfrac{15\sqrt{2}}{7}\left(cm\right)⇒AD=7152​​(cm).

Giải:

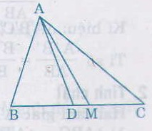
Ta có AD là đường phân giác của ∆ ABC nên

$\frac{S_{ABD}}{S_{ADC}}$ = $\frac{AB}{AC}$ = $\frac{m}{n}$(kết quả ở bài 16)

=> $\frac{S_{ABD}}{S_{ADC}+S_{ABD}}$= $\frac{m}{n+m}$

hay $\frac{S_{ABD}}{S_{ABC}}$= $\frac{m}{n+m}$ => $S_{ABM}$= $\frac{1}{2}$ $S_{ABC}$.

Giả sử AB < AC( m<n) vì AD là đường phân giác, AM là đường trung tuyến kẻ từ A nên AD nằm giữa AB và AM.

=> $S_{ADM}$= $S_{ABM}$ - $S_{ABD}$

=> $S_{ADM}$ = $\frac{1}{2}$S -$\frac{m}{n+m}$S =

a)

Có AB < AC (vì n > m) (1)

Ta có: \(\dfrac{AB}{AC}=\dfrac{BD}{DC}\) ( vì AD là phân giác của góc BAC) (2)

Từ (1) và (2), ta có BD < CD

⇒ D nằm giữa B và M

Đặt S₁, S₂ lần lượt là diện tích △ADM và △ADC

Ta có: \(\dfrac{S_1}{S_2}=\dfrac{\dfrac{1}{2}.BD.AH}{\dfrac{1}{2}.CD.AH}=\dfrac{BD}{CD}=\dfrac{AB}{AC}=\dfrac{m}{n}\)

⇒ \(\dfrac{S_1+S_2}{S_2}=\dfrac{m+n}{n}=\dfrac{S}{S_2}=\dfrac{m+n}{n}\Rightarrow S_2=\dfrac{n.S}{m+n}\)

Vì \(S_{AMC}=S_{AMB}=\dfrac{1}{2}.S\Rightarrow\)diện tích của △ADM là

\(S_{ADM}=S_{ADC}-S_{AMC}=S_2-\dfrac{1}{2}.S=\dfrac{n.S}{m+n}-\dfrac{1}{2}.S=\left[\dfrac{n-m}{2\left(m+n\right)}\right].S\)

b)

\(S_{ADM}=\left[\dfrac{7-3}{2\left(7+3\right)}\right].S=\dfrac{2}{10}.S=\dfrac{1}{5}.S=0,2.S=20\%.S\)

Vậy diện tích của △ADM bằng 20% diện tích của △ABC