Tìm số nguyên tố p sao cho các số sau cũng là số nguyên tố:
p +14 và p + 40.
Bài1:Các số sau là nguyên tố hay hợp số
a) 123456789 + 729
b) 5.7.8.9.11-132
Bài 2: Tìm số nguyên tố sao cho
a)P+2 và P+4 cũng là số nguyên tố
b)P+10 và P+14 cũng là số nguyên tố
Bài 1 :
a) \(123456789+729=\text{123457518}⋮2\)
⇒ Số trên là hợp số
b)\(5.7.8.9.11-132=\text{27588}⋮2\)
⇒ Số trên là hợp số
Bài 2 :
a) \(P+2\&P+4\) ;à số nguyên tố
\(\Rightarrow\dfrac{P+2}{P+4}=\pm1\)
\(\Rightarrow\left[{}\begin{matrix}\dfrac{P+2}{P+4}=1\\\dfrac{P+2}{P+4}=-1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}P+2=P+4\\P+2=-P-4\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}0.P=2\left(x\in\varnothing\right)\\2.P=-6\end{matrix}\right.\)
\(\Rightarrow P=-3\)
Câu b tương tự
a,123456789+729=123457518(hợp số)
b,5x7x8x9x11-132=27588(hợp số)
Bài 2,
a,Nếu P=2=>p+2=4 và p+4=6 (loại)
Nếu P=3=>p+2=5 và p+4=7(t/m)
P>3 => P có dạng 3k+1 hoặc 3k+2(k ϵn,k>0)
Nếu p=3k+1=>p+2=3k+3 ⋮3( loại)
Nếu p=3k+2=>p+4=3k+6⋮3(loại)
Vậy p=3 thỏa mãn đề bài
b,Nếu p=2=>p+10=12 và p+14=16(loại)
Nếu p=3=>p+10=13 và p+14=17(t/m)
Nếu p >3=>p có dạng 3k+1 hoặc 3k+2
Nếu p=3k+1=>p+14=3k+15⋮3(loại)
Nếu p=3k+2=>p+10=3k+12⋮3(loại)
Vậy p=3 thỏa mãn đề bài.
Tìm các số nguyên tố p sao cho các số sau cũng là số nguyên tố: p+6 , p+8 , p+12 , p+14
Mình Nghĩ Câu Này Cũng Dễ Chứ Đâu Khó Đâu
Mình Không Cố í xúc phạm đâu
Câu này là p = 5
Câu Này Dễ Nên Mình Không Giải Chi Tiết Nha Bạn
tìm số p nguyên tố sao cho p+14 và p+20 cũng là các số nguyên tố
p = 3
Nếu là ở Violympic thì chỉ ra đáp án được thôi !
nếu p ko thể bằng 2 vì nếu p=2
thì p+14=2+14=16 suy ra ko phải số nguyên tố
p+20=2+20=22 suy ra cũng ko phải số nguyên tố
nếu p=3 thì
p+14=3+14=17 là số nguyên tố
p+20=3+20=23 cung là số nguyên tô
nếu p>3 thì mâu thuẫn với đề bài và ko tim ra được p
Tìm số nguyên tố p sao cho p+10 và p+14 cũng là các số nguyên tố
p = 3
Tham khảo cách giải baaif này ( . ) câu hỏi tương tự nha bạn .
Tìm số nguyên tố p, sao cho các số sau cũng là số nguyên tố: p+2, p+6, p+8, p+12, p+14
Thử `p=2`
`=>p+2=4(HS)`
`=>p=2`(loại).
Thử `p=3`
`=>p+12=15(HS)`
`=>p=3`(loại).
Thử `p=5`
`=>` \begin{cases}p+2=7(SNT)\\p+6=11(SNT)\\p+8=13(SNT)\\p+12=17(SNT)\\p+14=19(SNT)\\\end{cases}
`=>p=5(TM)`
Nếu `p>5` mà p là SNT
`=>p cancel{vdost} 5`
`=>p=5k+1,5k+2,5k+3,5k+4`
`+)p=5k+1=>p+14=5k+15 vdots 5`
`=>p=5k+1` (loại).
`+)p=5k+2=>p+8=5k+10 vdots 5`
`=>p=5k+2` (loại).
`+)p=5k+3=>p+12=5k+15 vdots 5`
`=>p=5k+3` (loại).
`+)p=5k+4=>p+6=5k+10 vdots 5`
`=>p=5k+4` (loại).
Vậy `p=5`
Tìm số nguyên tố p, sao cho các số sau cũng là số nguyên tố b) p 10 và p 20 ;c) p 2, p 6, p 8, p 12, p 14.
Tìm số nguyên tố p,sao cho các số sau cũng là số nguyên tố]
a) p+2 và 10+p
b) p+10 và p+20
c) p+2 ; p+6 ; p+8 ; p+12 ; p+14
Câu b:

Đến đoạn này cũng xét như câu a
Câu c:
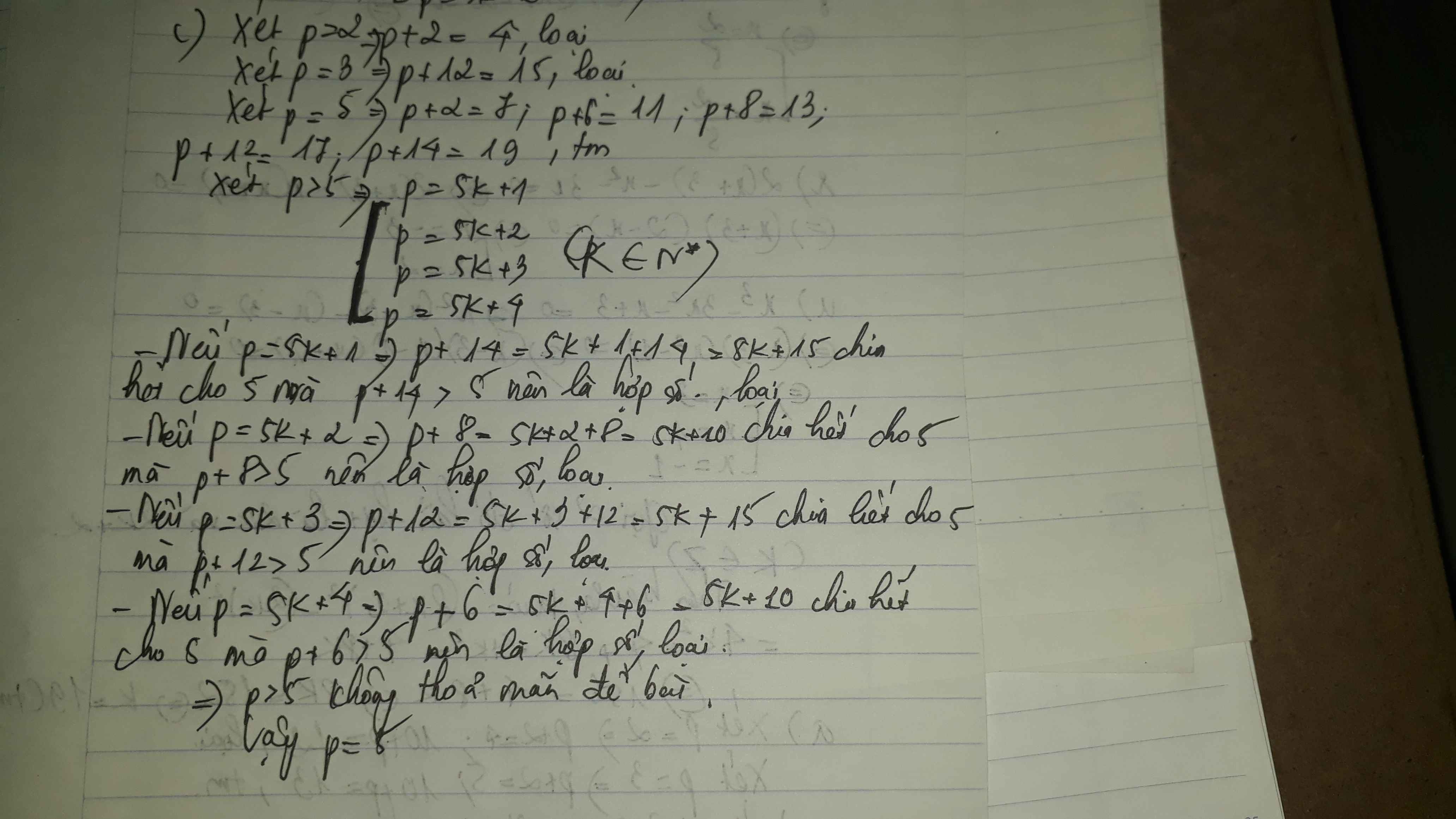
Tìm số nguyên tố p sao cho các số sau cũng là số nguyên tố:
p + 2; p + 8; p + 12; p + 14
tìm số nguyên tố p sao cho các số sau cũng là số nguyên tố p+6;p+8;p+12;p+14