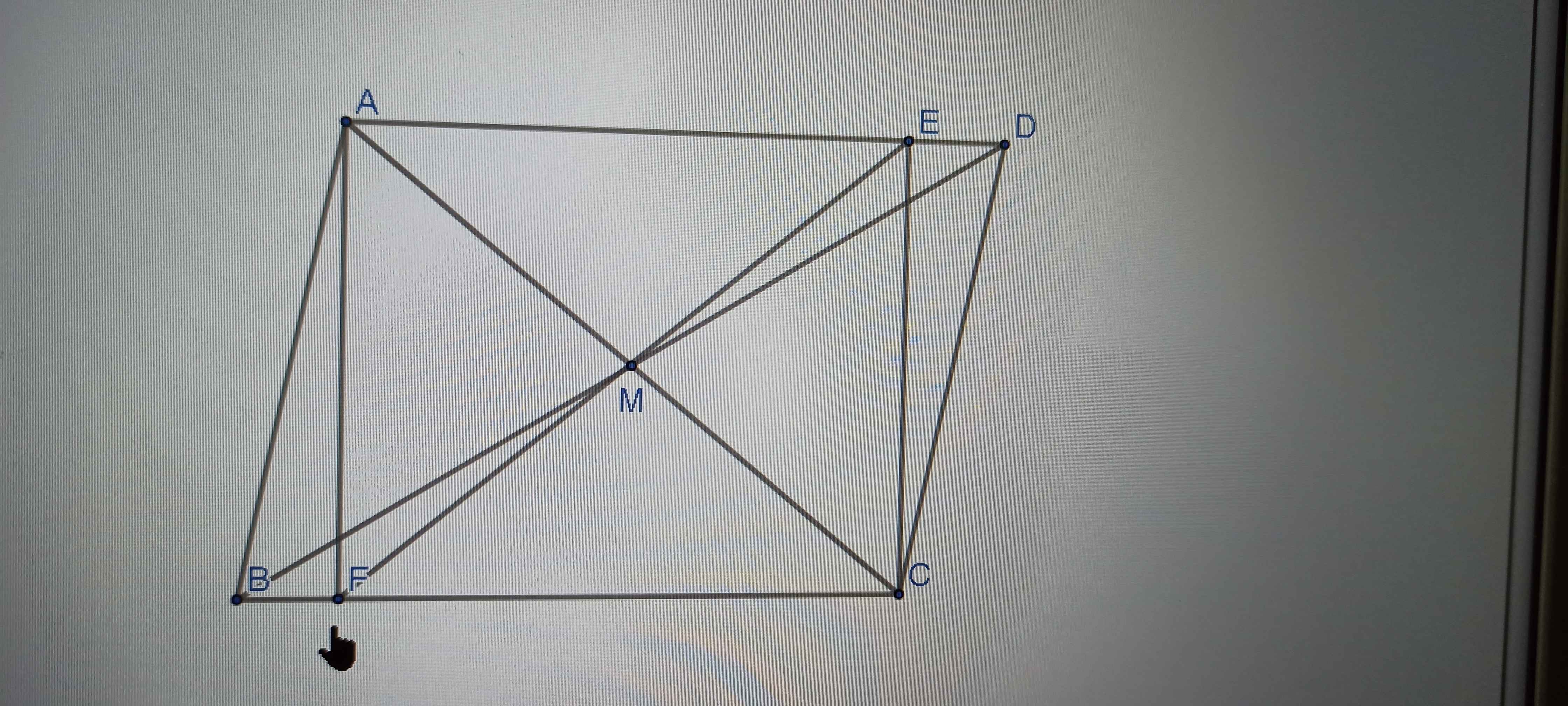
Cho tam giác ABC có 3 góc nhọn. M là 1 điểm trên cạnh BC. Gọi E; F lần lượt là hình chiếu của B; C trên AM. Xác định vị trí của M để tổng DE + CF lớn nhất. ai làm dùm mk sẽ tik cho😊. Làm nhanh dùm mk vs mk đang cần gấp!!!😭

Những câu hỏi liên quan
Cho tam giác ABC nhọn có AB<AC. Trên cạnh BC lấy điểm E sao cho AB=AE, gọi H là trung điểm của BE.
1. Chứng minh: tam giác ABH = tam giác AEH
2. Chứng minh AH vuông góc BE 3. Trên tia AH lấy điểm F sao cho AH = HF. Kẻ tia Ax // BC, trên Ax lấy điểm I sao cho AI = BE ( I cùng phía B so với đường thẳng AH )
a) Chứng minh: BF=AE
b) Chứng minh: 3 điểm I, B, F thẳng hàng
1: Xét ΔABH và ΔAEH có
AB=AE
BH=EH
AH chung
Do đó: ΔABH=ΔAEH
Đúng 2
Bình luận (0)
1: Xét ΔABH và ΔAEH có
AB=AE
BH=EH
AH chung
Do đó: ΔABH=ΔAEH
Đúng 1
Bình luận (0)
Cho tam giác ABC nhọn, M là trung điểm của AC. Trên tia đối của tia MB lấy điểm D sao cho MD = MB. Chứng minh:
a) tam giác MAB = tam giác MCD và AB // CD
b) góc ABC = góc CDA
c) Kẻ CE vuông góc với AD tại E. Gọi F là điểm trên cạnh BC sao cho BF = DE. Chứng minh À vuông góc với BC và 3 điểm F, M, E thẳng hàng
Câu C bạn cm AFCE là hình chữ nhật , FE là đường chéo => E,F,M thẳng hàng vì 2 đường chéo hình chữ nhật đi qua trung điểm của mỗi đường.
Đúng 0
Bình luận (0)
Cho tam giác ABC nhọn có AB < AC . Trên cạnh BC lấy điểm E sao cho
AB= AE, gọi H là trung điểm của BE.
1.
Chứng minh tam giác ABH=tam giác AEH.
2.
Chứng minh AH vuông góc BE
cho tam giác ABC nhọn, AB<AC .Trên cạnh AB lấy điểm D(D khác A và B),trên cạnh AC lấy điểm E sao cho góc ADE = ACB
a) CM : tam giác ADE đồng dạng tam giác ACB
b)Gọi i là giao điểm của BC và DE. CM: IB.IC=ID.IE
c)Lấy M là trung điểm BC . CM \(\dfrac{AD.AB}{AE.AM}\) =2
a: Xet ΔADE và ΔACB có
góc ADE=góc ACB
góc DAE chung
=>ΔADE đồng dạng với ΔACB
b: Xét ΔIDB và ΔICE có
góc IDB=góc ICE
góc I chung
=>ΔIDB đồng dạng với ΔICE
=>ID/IC=IB/IE
=>ID*IE=IB*IC
Đúng 0
Bình luận (0)
Cho tam giác ABC có 3 góc nhọn (AB<AC).Gọi M là trung điểm của BC trên tia AM lấy đimể E sao cho MA=ME a)Chứng minh tam giác AMB= tam giác EMC
Xét ΔAMB và ΔEMC có
MA=ME
\(\widehat{AMB}=\widehat{EMC}\)
MB=MC
Do đó: ΔAMB=ΔEMC
Đúng 0
Bình luận (0)
Xét ΔABM và ΔECM có:
BM = CM (do M là trung điểm của BC)
^AMB = ^EMC (2 góc đối đỉnh)
AM = EM (giả thiết)
=> ΔABM = ΔECm (c.g.c)
Đúng 0
Bình luận (0)
cho tam giác abc có 3 góc nhọn gọi M là điểm bất kì trên cạnh BC. gọi D là điểm đối xứng M qua AB,E là điểm đối xứng M qua AC. Gọi I là giao điểm của DE với AB, K là giao điểm của DE với AC
a) CM; AD=AE
b) CM: góc MA là phân giác của góc YMK
cho tam giác nhọn ABC . M là trung điểm của cạnh AC .Trên tia đối của tia MB lấy điểm D sao cho MD = MB . Qua điểm vẽ đường thẳng vuông góc với AD tại E . Gọi F là điểm thuộc cạnh BC sao cho BF = DE . CMR
a) tam giác AMD = tam giác CMB
b) Tam giác ABC = tam giác CDA
c) AF vuông goác với BC
d) ba điểm M,E,F thẳng hàng
a: Xét ΔAMD và ΔCMB có
MA=MC
góc AMD=góc CMB
MD=MB
=>ΔAMD=ΔCMB
b: Xét ΔABC và ΔCDA có
AB=CD
BC=DA
AC chung
=>ΔABC=ΔCDA
c: Sửa đề: MF vuông góc BC
Xét ΔMBF và ΔMDE có
MB=MD
góc MBF=góc MDE
BF=DE
=>ΔMBF=ΔMDE
=>góc MFB=90 độ
=>MF vuông góc BC
d: ΔMFB=ΔMED
=>góc FMB=góc EMD
=>góc EMD+góc DMF=180 độ
=>M,E,F thẳng hàng
Đúng 0
Bình luận (0)
Cho tam giác nhọn ABC. Điểm M là trung điểm của cạnh AC. Trên tia đối của MB lấy điểm D sao cho MD = MB. Qua điểm C vẽ đường thẳng vuông góc với AD tại E. Gọi F là điểm thuộc cạnh BC sao cho BF = DE. Chứng minh rằng:
a, tam giác AMD bằng tam giác CMB
b, tam giác ABC bằng tam giác CDA
c, AF vuông góc với BC
d, 3 điểm M, E ,F thẳng hàng
Bài 1: Cho tam giác ABC cân tại A có đường phân giác CD. Qua D kẻ tia DF vuông góc với DC; DE song song với BC ( F thuộc BC; E thuộc AC ). Gọi M là giao điểm của DE với tia phân giác của góc BAC. CMR:1) CF 2BD2) DM 1/4 CF Bài 2: Cho tam giác ABC cân tại A. Trên cạnh BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BDCE. Các đường thẳng vuông góc BC kẻ từ D và E cắt AB và AC lần lượt ở M và N. CMR:1) DMEN2) Đường thẳng BC cắt MN tại I là trung điểm của MN3) Đường thẳng vuông góc với MN...
Đọc tiếp
Bài 1: Cho tam giác ABC cân tại A có đường phân giác CD. Qua D kẻ tia DF vuông góc với DC; DE song song với BC ( F thuộc BC; E thuộc AC ). Gọi M là giao điểm của DE với tia phân giác của góc BAC. CMR:
1) CF= 2BD
2) DM= 1/4 CF
Bài 2: Cho tam giác ABC cân tại A. Trên cạnh BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD=CE. Các đường thẳng vuông góc BC kẻ từ D và E cắt AB và AC lần lượt ở M và N. CMR:
1) DM=EN
2) Đường thẳng BC cắt MN tại I là trung điểm của MN
3) Đường thẳng vuông góc với MN tại I luôn đi qua một điểm cố định khi D thay đổi trên cạnh BC
Bài 3: Cho tam giác ABC nhọn. Về phía ngoài của tam vẽ các tam giác vuông cân ABD và ACE đều vuông tại A. Gọi M và N lần lượt là trung điểm của BD và CE, P là trung trung điểm của BC. CMR: Tam giác PMN vuông cân
Cho tam giác nhọn ABC, trên cạnh BC lấy các điểm E,F sao cho góc BAE bằng góc CAF, gọi M, N lần lượt là hình chiếu vuông góc của F trên các đường thẳng AB và AC, kéo dài AE cắt đường tròn ngoại tiếp tam giác ABC tại D. Chứng minh rằng tứ giác AMDN và tam giác ABC có diện tích bằng nhau
Có vẻ bài này hơi không phù hợp với học sinh lớp 9. Đầu tiên ta sẽ phải sử dụng định lý sin cho tam giác: Trong tam giác ABC với bán kính đường tròn ngoại tiếp R thì tỷ số giữa cạnh và sin góc đối diện bằng 2R. Nhận xét tiếp theo: Diện tích tam giác bất kỳ một nửa tích độ dài hai cạnh nhân với sin của góc xen giữa hai cạnh đó.
Ta có \(S\left(ABC\right)=S\left(ABF\right)+S\left(ACF\right)=\frac{1}{2}AB\cdot AF\cdot\sin BAF+\frac{1}{2}AC\cdot AF\cdot\sin CAF\)
\(=\frac{1}{2}AB\cdot\frac{CD}{2R}\cdot AF+\frac{1}{2}AC\cdot AF\cdot\frac{BD}{2R}=\frac{AF}{4R}\left(AB\cdot CD+AC\cdot BD\right).\) Do tứ giác ABDC nội tiếp nên theo định lý Ptoleme ta có \(AB\cdot CD+AC\cdot BD=AD\cdot BC.\) LSuy ra \(S\left(ABC\right)=\frac{AF\cdot AD\cdot BC}{4R}.\)
Tiếp theo ta có \(S\left(AMDN\right)=S\left(AMD\right)+S\left(ADN\right)=\frac{1}{2}AM\cdot AD\cdot\sin BAD+\frac{1}{2}AD\cdot AN\cdot\sin DAC\)
\(=\frac{1}{2}AF\cdot\cos DAC\cdot AD\cdot\sin BAD+\frac{1}{2}AD\cdot AF\cdot\cos BAD\cdot\sin DAC\)
\(=\frac{1}{2}AF\cdot AD\cdot\left(\cos DAC\cdot\sin BAD+\sin DAC\cdot\cos BAD\right)=\frac{1}{2}\cdot AF\cdot AD\sin\left(DAC+BAD\right)\)
\(=\frac{1}{2}AF\cdot AD\cdot\sin BAC=\frac{1}{2}AF\cdot AD\cdot\frac{BC}{2R}=\frac{AF\cdot AD\cdot BC}{4R}.\)
Ở đây ta sử dụng công thức hình chiếu \(\sin\left(a+b\right)=\sin a\cos b+\cos a\sin b.\)
Vậy ta có tứ giác AMDN và tam giác ABC cùng diện tích.
Đúng 0
Bình luận (0)
Karin Korano
câu hỏi này của lớp 11 nhé !
1 cách trình bày khác; ngắn gọn hơn nha Thầy Giáo Toán
đặt ^BAE=^CAE=α; EAF=β
Ta có S∆ABC =1/2.AB.AF.sin(α+β)+1/2 .AC.AF sin α =AF/4R (AB.CD+AC.BD)
(R-là bán kính đường tròn ngoại tiếp tam giác ABC) (1)
Diện tích tứ giác ADMN là
SADMN =1/2.AM.AD.sin α +1/2AD.AN.sin(α+β) = 1/2.AD.AF.sin(2α +β) =AF/4R.AD.BC (2)
Vì tứ giác ABDC nội tiếp trong đường tròn nên theo định lí Ptoleme ta có
: AB.CD + AC.BD = AD.BC (3).
Từ (1), (2), (3) ta có điều phải chứng minh