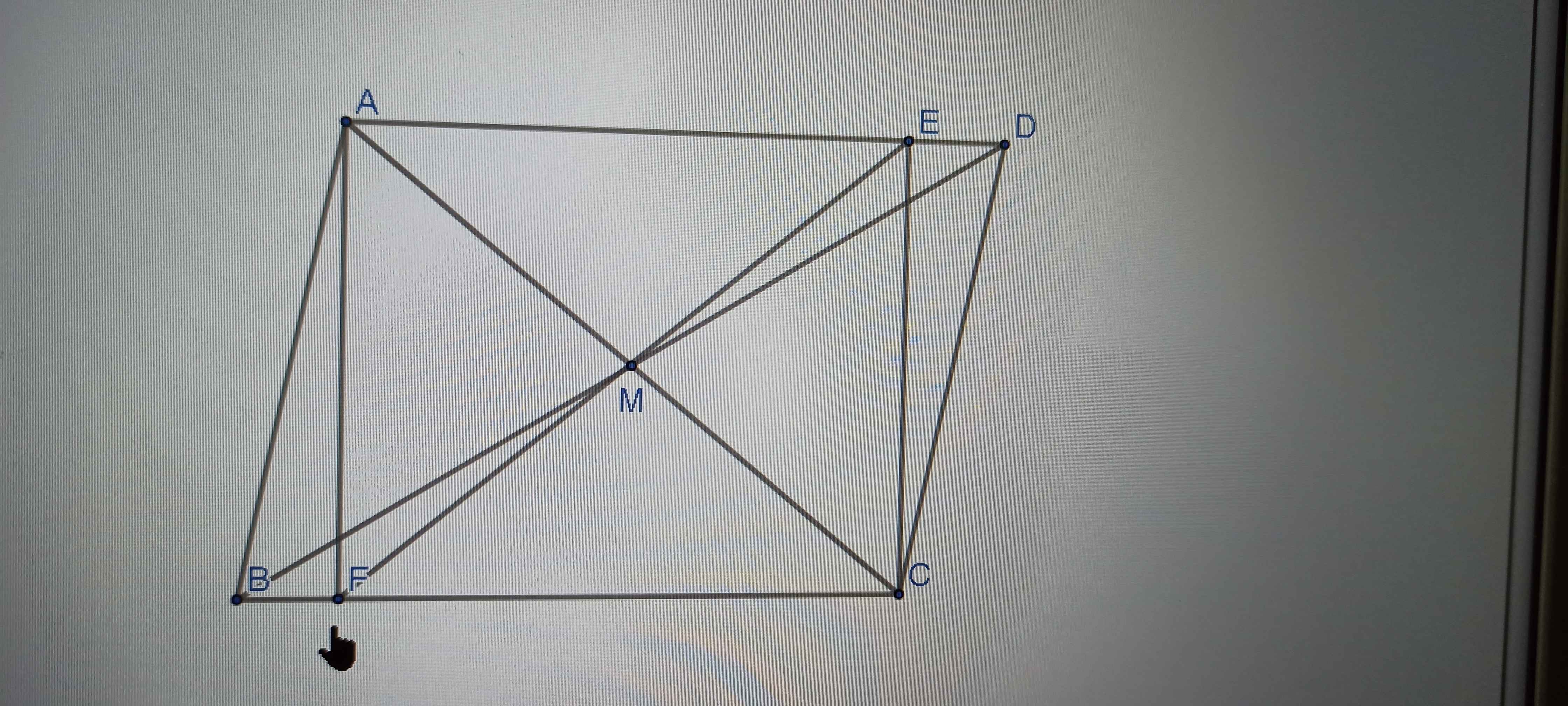
Cho tam giác ABC nhọn, M là trung điểm của AC. Trên tia đối của tia MB lấy điểm D sao cho MD = MB. Chứng minh:
a) tam giác MAB = tam giác MCD và AB // CD
b) góc ABC = góc CDA
c) Kẻ CE vuông góc với AD tại E. Gọi F là điểm trên cạnh BC sao cho BF = DE. Chứng minh À vuông góc với BC và 3 điểm F, M, E thẳng hàng
Câu C bạn cm AFCE là hình chữ nhật , FE là đường chéo => E,F,M thẳng hàng vì 2 đường chéo hình chữ nhật đi qua trung điểm của mỗi đường.