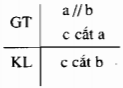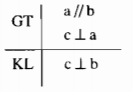CM định lí nếu 1đt vuông góc cắt 1 trong 2 đt song song thì nó cx vuông góc với đt còn lại

Những câu hỏi liên quan
Cho tam giác ABC, góc A=90 độ, AB<AC, từ B vẽ đt vuông góc với AB, Từ C vẽ đt thẳng vuông góc với AC, 2 đt này cắt nhau tại D, AD cắt BC tại
a) Cm AI =1/2 BC
b) kẻ AH vuông góc với BC tại H. Cm góc AHI=ABC\(-\)ACB
c) Qua D vẽ đt song song với BC cắt AH tại M. Cm góc BMC=90 độ
Chứng minh các định lí sau:
a) Cho hai mặt phẳng song song. Nếu một mặt phẳng vuông góc với một trong hai mặt phẳng đó thì vuông góc với mặt còn lại;
b) Nếu hai mặt phẳng (phân biệt) cùng vuông góc với mặt phẳng thứ ba thì song song với nhau hoặc cắt nhau theo một giao tuyến vuông góc với mặt phẳng thứ ba đó.
a)
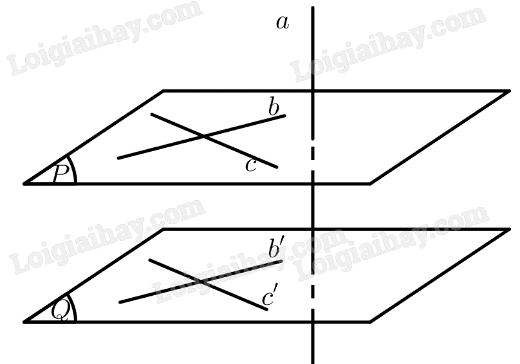
Cho hai mặt phẳng \(\left( P \right),\left( Q \right)\) song song với nhau và đường thẳng \(a\) vuông góc với \(\left( P \right)\). Ta cần chứng minh \(a \bot \left( Q \right)\).
Trên \(\left( P \right)\) lấy hai đường thẳng \(b,c\) cắt nhau, trên \(\left( Q \right)\) lấy hai đường thẳng \(b',c'\) sao cho \(b'\parallel b,c'\parallel c\).
Vì \(b,c\) cắt nhau nên \(b',c'\) cắt nhau.
\(\begin{array}{l}\left. \begin{array}{l}a \bot \left( P \right) \Rightarrow a \bot b,a \bot c\\b\parallel b',c\parallel c'\end{array} \right\} \Rightarrow a \bot b',a \bot c'\\ \Rightarrow a \bot \left( Q \right)\end{array}\)
Đúng 0
Bình luận (0)
b)
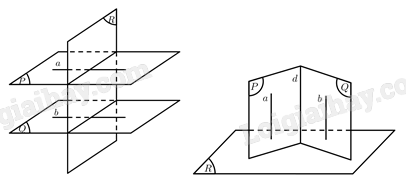
Cho hai mặt phẳng \(\left( P \right),\left( Q \right)\) cùng vuông góc với mặt phẳng \(\left( R \right)\). Ta cần chứng minh \(\left( P \right)\parallel \left( Q \right)\) hoặc \(d \bot \left( R \right)\) với \(d = \left( P \right) \cap \left( Q \right)\).
Vì \(\left( P \right) \bot \left( R \right)\) nên tồn tại đường thẳng \(a \subset \left( P \right)\) sao cho \(a \bot \left( R \right)\), \(\left( Q \right) \bot \left( R \right)\) nên tồn tại đường thẳng \(b \subset \left( Q \right)\) sao cho \(b \bot \left( R \right)\)
\( \Rightarrow a\parallel b\)
Vậy \(\left( P \right)\parallel \left( Q \right)\) hoặc nếu \(\left( P \right),\left( Q \right)\) cắt nhau theo giao tuyến \(d\) thì \(d\parallel a \Rightarrow d \bot \left( R \right)\).
Đúng 0
Bình luận (0)
vẽ hình và viết giả thiết kết luận của các định lí sau :
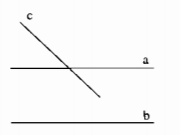
a) Nếu 1 đường thẳng cắt 1 trong 2 đường thẳng somg song thì nó cắt đuồng thẳng kia
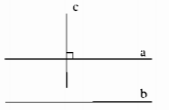
b) Nếu 1 đường thẳng vuông góc với 1 trong 2 đường thẳng song song thì nó cũng vuông góc với đường thẳng kia
a) Giả thiết : Nếu 1 đường thẳng cắt 1 trong 2 dường thẳng song song
Kết luận: thì nó cắt đường thẳng kia
b) Giả thiết : Nếu 1 đường thẳng vuông góc với 1 trong hai đường thẳng song song
Kết luận : thì nó cũng vuông góc với đường thẳng kia
CHÚC BẠN HỌC TỐT NHA !
Đúng 0
Bình luận (0)
Vẽ hình, viết giả thiết, kết luận bằng kí hiệu và chứng minh định lí: " Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng sẽ vuông góc với đường thẳng còn lại."
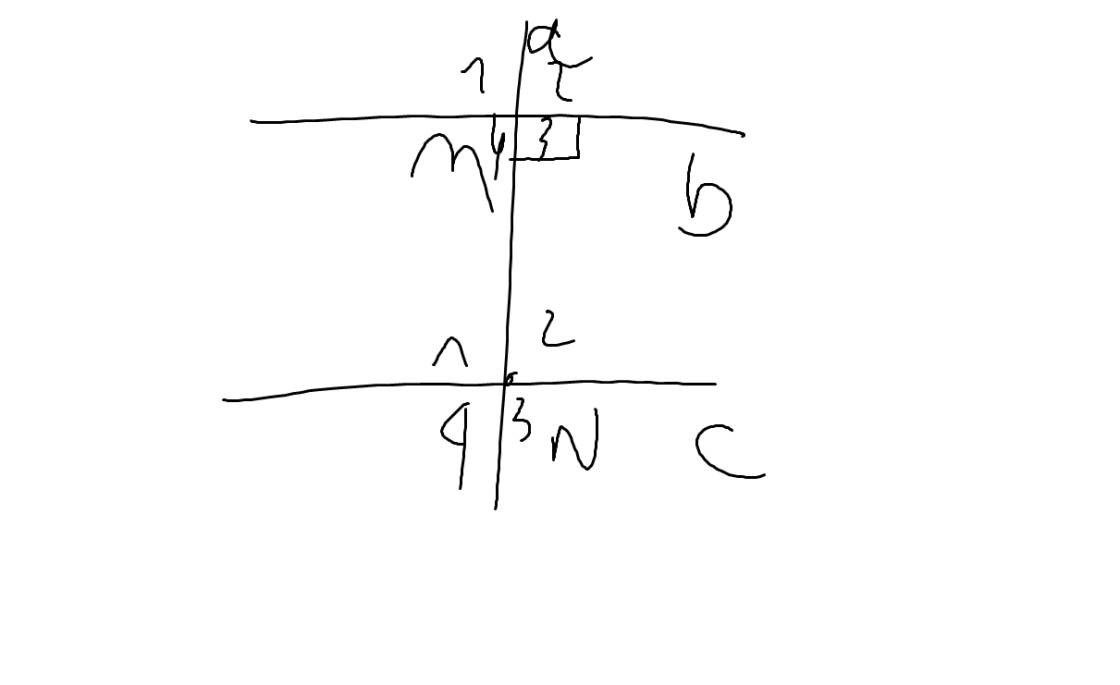
| GT | a\(\perp\)b tại M a cắt c tại N b//c |
| KL | a\(\perp\)c tại N |
Chứng minh định lí:
Ta có: b//c
=>\(\widehat{M_3}=\widehat{N_1}\)(hai góc so le trong)
mà \(\widehat{M_3}=90^0\)
nên \(\widehat{N_1}=90^0\)
=>a\(\perp\)c tại N
Đúng 0
Bình luận (0)
bài 1: vẽ hình và viết GT,KL các định lí sau bằng kí hiệu.a) Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cùng vuông góc với đường thẳng kiab) Nếu 1 đường thẳng cắt hai đường thẳng song song thì 2 góc đồng vị bằng nhaumong các bạn giúp đỡ
Đọc tiếp
bài 1: vẽ hình và viết GT,KL các định lí sau bằng kí hiệu.
a) Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cùng vuông góc với đường thẳng kia
b) Nếu 1 đường thẳng cắt hai đường thẳng song song thì 2 góc đồng vị bằng nhau
mong các bạn giúp đỡ
Vẽ hình, viết giả thiết, kết luận của định lí: “ Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng còn lại”.

Giả sử cho 2 đường thẳng song song a và b, đường thẳng c vuông góc với a. Ta phải chứng minh c cũng vuông góc với b.
Thật vậy,
Vì a//b nên \(\widehat {{A_1}} = \widehat {{B_1}}\) ( 2 góc đồng vị), mà \(\widehat {{A_1}} = 90^\circ \)nên \(\widehat {{B_1}} = 90^\circ \) hay \(b \bot c\)(đpcm)
Đúng 1
Bình luận (0)
Vẽ hình và viết giả thiết, kết luận của các định lí sau :
a) Nếu một đường thẳng cắt một trong hai đường thẳng song song thì nó cắt đường thẳng kia
b) Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng kia
vẽ hình và viết giả thiết, kết luận của các định lí sau :
a) nếu 1 đường thẳng trong 2 đường thẳng song song thì nó cắt đường thẳng kia
b) nếu một đường thẳng vuông góc với một trong hai đường thẳng songsong thì nó cũng vuông góc với đường thẳng kia
Vẽ hình thì dựa theo trong sách có nhé bạn!
a/ Bài a của bạn mình đọc không hiểu lắm hình như viết sai đề phải không bạn?
b/ GT: a song song với b,
c vuông góc với a
KL: c vuông góc với b
CẢM ƠN ĐÃ ĐỌC ĐÁP ÁN CỦA MÌNH
Đúng 0
Bình luận (0)
Chứng minh định lý:
Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng còn lại.
Từ t/c :
Nếu đường thẳng a và đường thẳng b cùng vuông góc với 1 đường thẳng thì hai đường thẳng a và đường thẳng b song song với nhau.
=> đpcm.
Đúng 1
Bình luận (0)
Ta có : \(x||y\left(gt\right)\)
\(\Rightarrow\widehat{A_1}=\widehat{B_1}\)( hai góc so le trong )
Mà \(\widehat{A_1}=90^o\)
\(\Rightarrow\widehat{B_1}=90^o\)
Hay \(AB\perp y\)
Đúng 1
Bình luận (0)