Cho tam giác ABC và một điểm M trong tam giác này. Gọi E, F, I, K theo thứ tự là trung điểm của AB, AC, MC, MB.
a) Chứng minh tứ giác KEFI là hình bình hành.
b) Xác định vị trí của điểm M để KEFI là hình chữ nhật.
Cho tam giác ABC và một điểm M trong tam giác này. Gọi E, F, I, K theo thứ tự là trung điểm của AB, AC, MC, MB.
a) Chứng minh tứ giác KEFI là hình bình hành.
b) Xác định vị trí của điểm M để KEFI là hình chữ nhật
a) xét tam giác ABC, có:
E là trung điểm AB (gt)
F là trung điểm AC (gt)
=> EF là đtb (đường trung bình) tam giác ABC
=> EF // BC (1)
xét tam giác BMC, có:
K là trung điểm BM (gt)
I là trung điểm MC (gt)
=> KI là đtb tam giác BMC
=> KI // BC (2)
từ (1),(2):
=> EF // KI
ta có: EF là đtb (cmt)
=>EF = \(\frac{BC}{2}\)(3)
ta có: KI là đtb (cmt)
=> KI = \(\frac{BC}{2}\)(4)
từ (3),(4):
=> EF = KI
ta có: EF // KI (cmt)
EF = KI (cmt)
=> EFIK là hbh (tứ giác có 1 cặp cạnh đối vừa = nhau vừa //)
b) chưa biết làm :V
Cho tam giác ABC gọi m, n theo thứ tự là trung điểm của các đoạn thẳng AB,AC a. Tính độ dài cạnh BC .biết MN = 2,5 b. Gọi I,k theo thứ tự là trung điểm của các đường thẳng MC ,MB chứng minh tứ giác mnik là hình bình hành . c. Tam giác abc phải có thêm điều kiện gì để tứ giác mnik là hình chữ nhật vì sao
a: Xét ΔABC có AM/AB=AN/AC
nên MN//BC và MN=BC/2
=>BC=5cm
b: Xét ΔMBC có
MK/MB=MI/MC
nên KI//BC và KI=BC/2
=>MN//KI và MN=KI
=>MNIK là hình bình hành
Cho tam giác ABC gọi M,N,I,K theo thứ tự là trung điểm của các đoạn thẳng AB,AC,MB,MC a. Biết MN=2.5 cm. Tính độ dài cạnh BC b. Chứng minh tứ giác MNIK là hình bình hành c. Tam giác ABC phải có thêm điều kiện gì để tứ giác MNIK là hình chữ nhật? Vì sao? d. Cho biết S abc=a, tính S amn theo a
a. Vì M,N là trung điểm AB,AC nên MN là đtb tg ABC
Do đó BC=2MN=5(cm)
b. Vì MN là đtb tg ABC nên \(MN=\dfrac{1}{2}BC;MN\text{//}BC\left(1\right)\)
Vì I,K là trung điểm MB,MC nên IK là đtb tg MBC
Do đó \(IK=\dfrac{1}{2}BC;IK\text{//}BC\left(2\right)\)
\(\left(1\right)\left(2\right)\Rightarrow MN=IK;MN\text{//}IK\\ \Rightarrow MNIK\text{ là hbh}\)
c. Để MNIK là hcn thì \(MI\bot MN\)
Mà \(MI\equiv AB;MN\text{//}BC\Leftrightarrow AB\bot BC\)
Vậy ABC vuông tại A thì MNIK là hcn
d. Kẻ đường cao AH của tam giác ABC và AMN
Do đó \(\dfrac{S_{ABC}}{S_{AMN}}=\dfrac{\dfrac{1}{2}AH\cdot BC}{\dfrac{1}{2}AH\cdot MN}=\dfrac{BC}{MN}=2\)
\(\Rightarrow S_{AMN}=\dfrac{1}{2}S_{ABC}=\dfrac{a}{2}\)
Cho tam giác ABC. Gọi O là một điểm thuộc miền trong của tam giác. M, N, P, Q lần lượt là trung điểm của các đoạn thẳng OB, OC, AC, AB.
a) Chứng minh tứ giác MNPQ là hình bình hành.
b) Xác định vị trí của điểm O để tứ giác MNPQ là hình chữ nhật
a) HS tự chứng minh
b) O nằm trên đường cao xuất phát từ đỉnh A của DABC
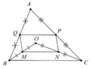
Cho tam giác ABC , đường cao AH . Gọi M là trung điểm của cạnh BC . Qua M kẻ các đường thẳng song song với AB và AC , chúng cắt các cạnh AC và AB theo thứ tự tại E và D .
a) Cmr : Tứ giác ADME là hình bình hành . Gọi O là giao điểm của AM và DE . Cmr : Tam giác OAH cân .
b) Tứ giác tạo thành từ 4 điểm D , E , M , H là hình gì ? Tại sao ?
c) Tìm điều kiện của tam giác ABC để tứ giác ADME là hình chữ nhật .
Trong trường hợp này hãy xác định vị trí của điểm M trên cạnh BC để độ dài đoạn thẳng DE nhỏ nhất
1) ADME là h.b.h (vì có 2 cặp cạnh đối song song)
2) Vì ADME là hình chữ nhật nên O là trung điểm 2 đường chéo AM và DE.
Xét tam giác AHM vuông tại H, đường trung tuyến HO, khi đó HO = AO = OM
Vậy tam giác AHO cân ở O
3)
a, Tam giác ABC vuông tại A nên ˆDAE=900DAE^=900
Mà ADME là h.b.h nên tứ giác ADME là hình chữ nhật
b, Vì tứ giác AEMD là hình chữ nhật nên ED=AM
Để DE có độ dài nhỏ nhất thì AM có độ dài nhỏ nhất hay M là chân đường vuông góc hạ từ A xuống BC
Bài 2: Cho tam giác ABC. Gọi O là một điểm thuộc miền trong của tam giác, M, N, P, Q lần lượt là trung điểm của các đoạn thẳng OB, OC, AC, AB.
a) Chứng minh tứ giác MNPQ là hình bình hành
b) Xác định vị trí của điểm O để tứ giác MNPQ là hình chữ nhật
Cho tam giác ABC , đường cao AH . Gọi M là trung điểm của BC . Qua M kẻ các đường thẳng song song với AB và AC, chúng cắt các cạnh AC và AB theo thứ tự tại E và D.
a, CMR: Tứ giác ADME là hình bình hành. Gọi O là giao điểm của AM và DE. CM: tam giác OAH cân
b, Tứ giác tạo thành từ 4 điểm D, E, M ,H là hình gì ? Tại sao ?
c,Tìm điều kiện của tam giác ABC để tứ giác ADME là hình chữ nhật
Trong trường hợp này hãy xác định vị trí của điểm M trên cạnh BC để độ dài đoạn thẳng DE nhỏ nhất.
Cứu mình với mình sắp phải nộp bài rồi !!
Bài 4. Cho tam giác ABC. Gọi O là một điểm thuộc miền trong của tam giác, M,
N, P, Q lần lượt là trung điểm của các đoạn thẳng OB, OC, AC, AB.
a) Chứng minh tứ giác MNPQ là hình bình hành.
b) Xác định vị trí của điểm O đế tứ giác MNPQ là hình chữ nhật.
o giả thiết cho IJ không song song với CDvà chúng cùng nằm trong mặt phẳng (BCD) nên khi kéo dài chúng gặp nhau tại một điểm.
Gọi K=IJ∩CDK=IJ∩CD.
Ta có : M là điểm chung thứ nhất của (ACD) và (IJM);
{K∈IJIJ⊂(MIJ)⇒K∈(MIJ){K∈IJIJ⊂(MIJ)⇒K∈(MIJ) và {K∈CDCD⊂(ACD)⇒K∈(ACD){K∈CDCD⊂(ACD)⇒K∈(ACD)
Vậy (MIJ)∩(ACD)=MK(MIJ)∩(ACD)=MK
Quảng cáo
b) Với L=JN∩ABL=JN∩AB ta có:
{L∈JNJN⊂(MNJ)⇒L∈(MNJ){L∈JNJN⊂(MNJ)⇒L∈(MNJ)
{L∈ABAB⊂(ABC)⇒L∈(ABC){L∈ABAB⊂(ABC)⇒L∈(ABC)
Như vậy L là điểm chung thứ nhất của hai mặt phẳng (MNJ) và (ABC)
Gọi P=JL∩AD,Q=PM∩ACP=JL∩AD,Q=PM∩AC
Ta có:
{Q∈PMPM⊂(MNP)⇒Q∈(MNJ){Q∈PMPM⊂(MNP)⇒Q∈(MNJ)
Và {Q∈ACAC⊂(ABC)⇒Q∈(ABC){Q∈ACAC⊂(ABC)⇒Q∈(ABC)
Nên Q là điểm chung thứ hai của (MNJ) và (ABC)
Vậy LQ=(ABC)∩(MNJ)LQ=(ABC)∩(MNJ).
ko hiểu nhưng thôi k vậy >:(
sao lại có chữ quảng cáo vậy bạn?
cho tam giác ABC gọi O là điểm thuộc miền trong của tam giác. M,N,P,Q thứ tự là trung điểm cua OP,OC,AC,AB
Chứng minh:a) MNPQ là hình bình hành
b) Xác định vị trí điểm O để tứ giác MNPQ là hình chữ nhật